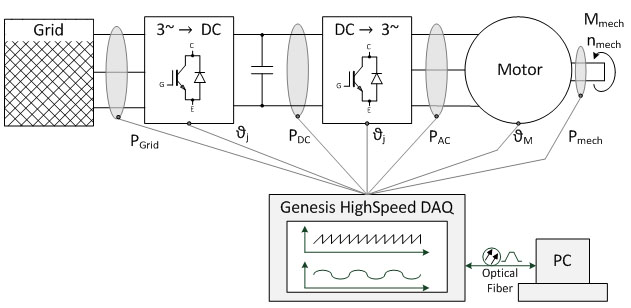
对于电能系统的测量来说,多种物理量必须记录,存储和调制,如图1.1采用的是三相驱动。 Genesis HighSpeed 数据记录仪能够对电能系统的所有重要物理量进行同步采集 - 多通道,极高采样率[1]。尤其是三相系统来说,采用空间矢量能够清楚地显示这些测量量并非常容易解释。空间矢量也可以用于表示静止操作状态和动平衡过程。在本文中,首先解释了空间矢量的定义公式和在不同坐标系下转换的规则。接着描述了如何采用空间矢量来表示永磁激励同步电机(PSM)的物理量。并采用 Perception 工作台[3] 来实现整个过程。
采用 Perception 软件,通过空间矢量,对电能测量量进行计算和实现
空间矢量通常用于简明扼要地表示电能转换系统例如变压器或感应电机的测量量。如果和时间相关的空间矢量以复平面轨迹曲线表示,这些电能转换系统的操作状态等信息就可以被测定。为了进一步简化这些测量量,空间矢量需要在旋转坐标系中表示。本文描述了如何使用 Perception 软件在不同坐标系中表示空间矢量,并采用永磁激励同步电机作为案例进行说明。
1. 简介
2.空间矢量
1959年 K.P. Kovács 发表了空间矢量理论来对三相系统进行数学描述。通常用于描述感应电机的控制方法。这样,在一定条件下,三相系统的电学和磁学量可被映射到一个两相正交系统和一个零序系统中。两相正交系统可被解释为空间矢量的复数。复数的实部和虚部以复平面的 α 和 β 轴来显示。公式 1.01 定义了三线变量X1,X2和X3进行复杂空间矢量 ![]() 计算规则:
计算规则:
![]()
α 是复转动参数. 相应的零序系统由以下公式计算
![]()
图 2.1a 显示了 空间矢量 ![]() 在正交坐标系。
在正交坐标系。
横坐标α表示空间矢量的实数部分,纵坐标β表示虚数部分。在该图中的坐标轴(α,β)是静止的。当旋转 120° a, b, c 时,线量可以通过空间矢量投影获得。
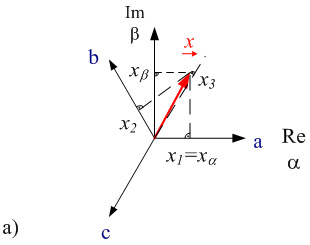
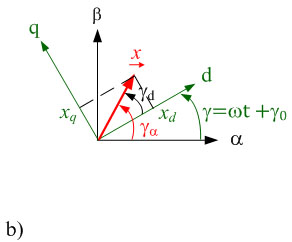
图2.1: 空间矢量在复平面 a) 实现,坐标系 α, β 在静止状态下, b) 在旋转坐标系下
Perception 软件提供转换三相量 (x1, x2, x3) 到空间矢量的预定义功能:

还提供了一个逆相变数学函数,来计算从空间矢量到相应的线量:
各种转换参数的含义在线帮助部分清晰描述,当输入公式时提示。
采用这些转换功能,计算可在空间向量域中执行。计算的结果可以再次以线量显示。
在很多应用中,旋转矢量坐标系可以提高结果的清晰性,并降低计算开销。目前,我们采用的是静止状态的 α 和 β 轴,也可以考虑 d,q 坐标系下的空间矢量,也就是旋转了相对应原始坐标系选择了时间依赖性角度γ(t)的坐标系。如果空间矢量是自极坐标下描述的化,转换规则推导非常简单。静止极坐标系的空间矢量如下:
![]()
如图所示 1.1b),这个空间矢量也可采用旋转坐标系的d和q轴描述。上标R表示该空间矢量在旋转坐标系下表示。在不同的坐标系下,极点显示量不会发生变化,只是角度需要调整。
![]()
空间矢量从一个坐标系到另外一个的转化,仅需乘以旋转因子 ejγ.
![]()
欧拉公式 ejγ = cos(γ)+j sin(γ) 可以用于计算旋转空间矢量的分量。
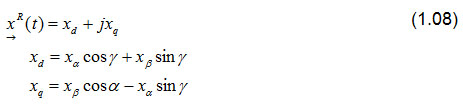
Perception 提供以下功能,用于三个线量 x1, x2 和 x3 到旋转空间矢量的转换。
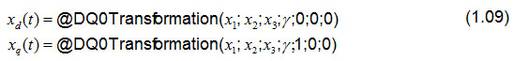
所需的转化的角 γ 可以通过计算或位置编码器读取,这取决于应用。
3. 永磁激励同步电机
在不同坐标系下空间矢量的转换通过以下永磁激励同步电机来进行说明 [4]。为保存描述的简单性,采用了一台各向同性同步电机。图 3.1a) 为一台表面安装的永磁同步电动机(PMSM)。这种类型的电机可被认为是大致各向同性的。在这里极对数量为 p=2。为获得电机更多的有用描述,实际的电机模型极对采用 p=1。 另外,我们必须考虑机械转速n与电气频率f 的相关性。


图3.1: a) PSM 基本布局 b) PSM 的空间矢量模型
如果位置编码器放置在电机轴上,需要获取极对数 p,偏移角度 γ0 和角度γ,才能进行矢量的转换计算。功能
在 Perception 软件中定义。偏置角γ0考虑了机械转子的北极和位置编码器零位置之间的偏移。
无负载测试用来确定偏置角γ0。要做到这一点,同步电机必须用轴来机械驱动。图 3.2 显示了星形电压U1,机械角度 γmech 通过位置编码器获取。偏移角度γ0可以从电压U1的负斜率的零交叉和位置编码器零点的时间偏移读取。
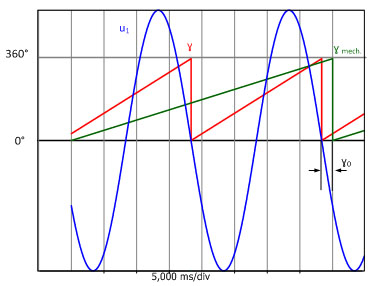
图 3.2: 星电压 u1 时间相关曲线, 机械角 γmech 和电能角 γ
无负载的星形电压如图3.3。如果电压的振幅相同,相位偏移为 120°,这三个正弦电压将形成对称三相系统。空间矢量分量(uα,uβ) 如图3.3a 显示为一个时间函数。由于是对称系统,这些空间矢量分量(uα,uβ)的相偏移为90°。
如果空间矢量分量采用xy表示,电压空间矢量将被描述为一个环形,如图3.3b。如果曲线的轨迹和理想圆有偏离,则可以一眼看出,这三个电压无法形成一个对称三相系统。
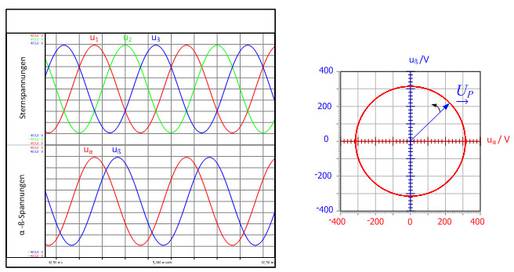
图. 3.3: 星电压 u1,u2 和u3 时间相关曲线,空间矢量分量 uα,uβ (左图)。电压空间矢量的轨迹(右图)
如果空间矢量分量 uα 和 uβ在一个旋转极坐标下以 ud 和 uq 表示,这些随时间变化的量将变成恒定量。对称三相系统的分量 ud 和 uq 如图3.4。一次时间函数,一次为复平面。

图. 3.4:时间相关曲线 a) 空间矢量分量 ud 和 uq 和
b) 在旋转坐标系下的电压空间矢量分量
总结
本文描述了采用 Genesis HighSpeed 数据记录仪和 Perception 软件采用空间矢量进行信号调理的过程。描述了在不同坐标系下空间矢量的计算,并形成原始数据。坐标系通过同步电机非负载测试来进行解释,并描述了在 Perception 中空间矢量的不同显示方法。在实际的测试中,HBM 提供了一个空间矢量的计算方法的工作台。
Bibliography
[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft [Electromobility in the fast lane: increased efficiency for the drive of the future]; proceedings of the 3rd conference of Innovation Messtechnik [Innovation in Measurement Technology]; May 14, 2013
[2] Berechnung von Leistungsgrößen mit Perception-Software
[Calculating power values with Perception software] https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/
[3] www.hbm.com
[4] J. Teigelkötter: Energieeffiziente elektrische Antriebe [Energy-efficient electric drives], 1st edition, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3