Klar und verständlich: Temperaturkompensation bei DMS-Viertelbrücken-Anwendungen

Diese Temperatureinflüsse können mit Softwarepaketen für Dehnungsmessstreifen-Anwendungen wie catman Easy/AP von HBK korrigiert werden. Wir liefern Ihnen eine klare, kurze und verständliche Verbindung von Theorie und Praxis der Temperaturkompensation bei DMS-Viertelbrücken-Anwendungen.

Dehnungsmessstreifen von HBK werden mit einem Datenblatt geliefert, das alle erforderlichen Parameter enthält, um die Genauigkeit der Messung zu gewährleisten. Das DMS-Datenblatt von HBK hat das folgende Layout und weist die Parameter für die Kompensation in einem Diagramm und einer Formel aus. Anmerkung: In diesem Beispiel werden im Datenblatt zwei Kurven gezeigt. Eine Kurve stellt den Temperaturgang des Dehnungs­mess­streifens selbst dar, während die andere Kurve das Temperaturverhalten des DMS mit 2 Anschlussbändchen darstellt.

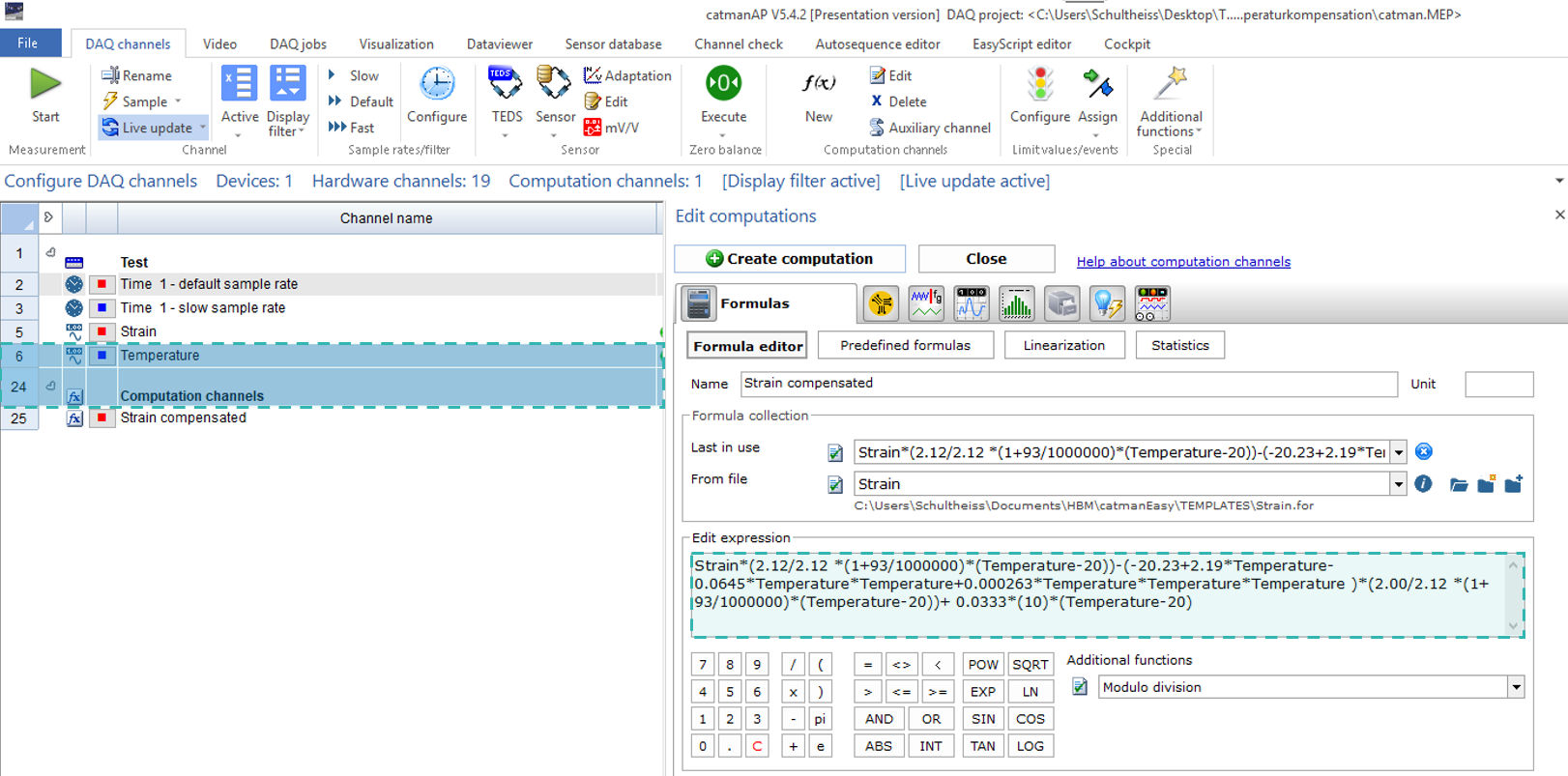
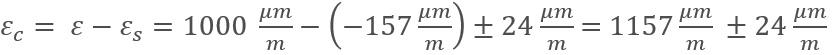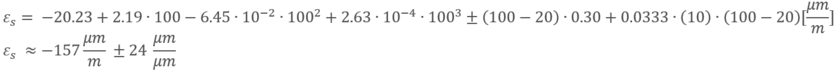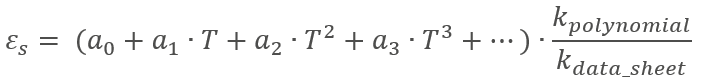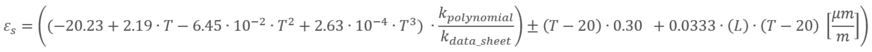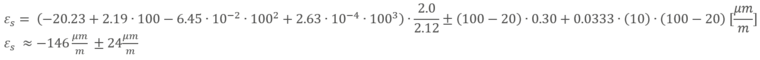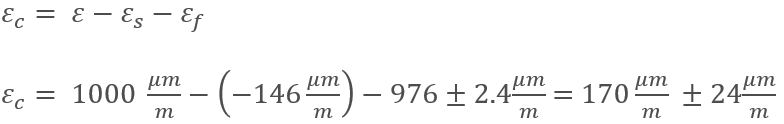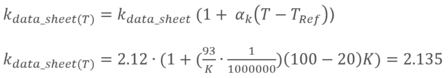In einigen Fällen enthält das Polynom weitere Faktoren, die bei Temperaturschwankungen das Dehnungssignal beeinflussen:

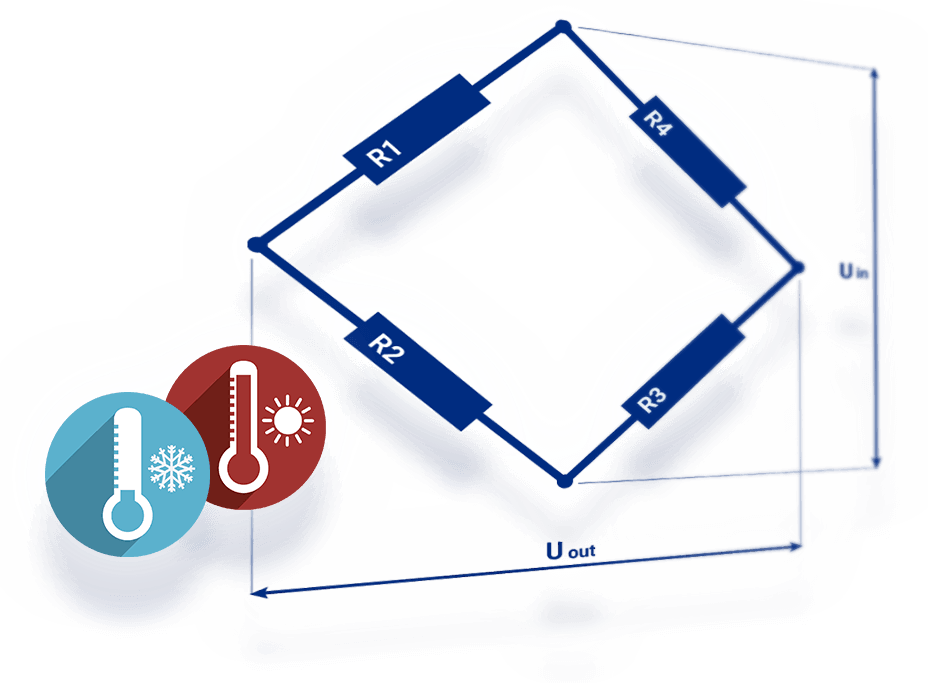
• Einfluss der Anschlussbändchen (ε_l): Im Allgemeinen muss auch der Einfluss der Anschlussbändchen berücksichtigt werden, der jedoch je nach DMS-Typ und Hersteller unterschiedlich sein. Wenn Sie unsere von HBM patentierte 3- oder 4-Leiter-Technik einsetzen, werden alle Kabelwiderstände kompensiert. In einigen Fällen gibt es jedoch einen Restanteil der 2-Leiter-Konfiguration, der nicht automatisch kompensiert werden kann.
• Messunsicherheit (ε_u): Die Messunsicherheit ist ein allgemeiner Bestandteil, der bei der Gesamtberechnung berücksichtigt werden sollte. Sogar das Polynom weist einiges an Streuung auf, die zu diesem Teil der Unsicherheit führt.

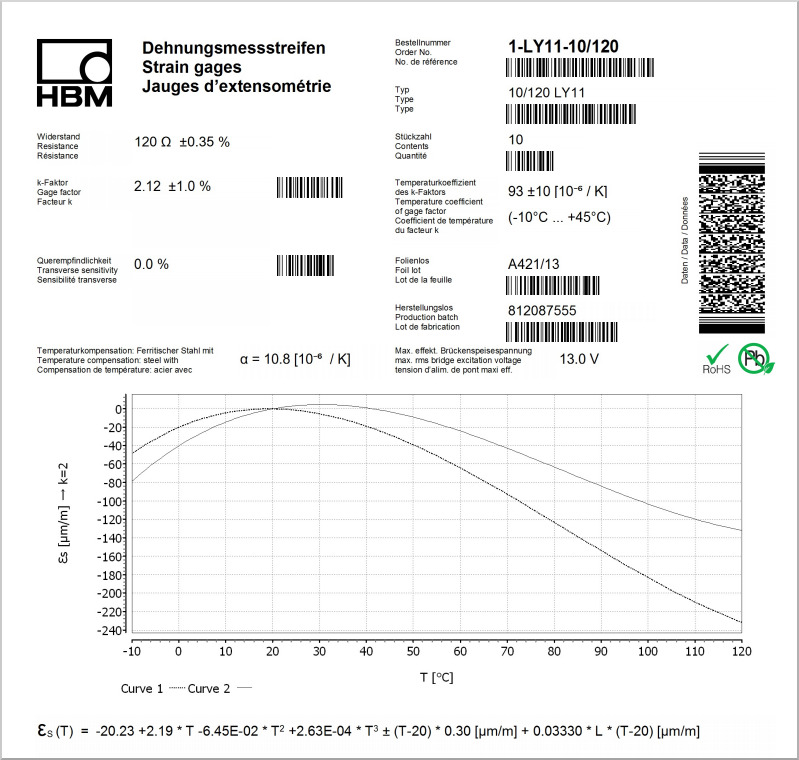
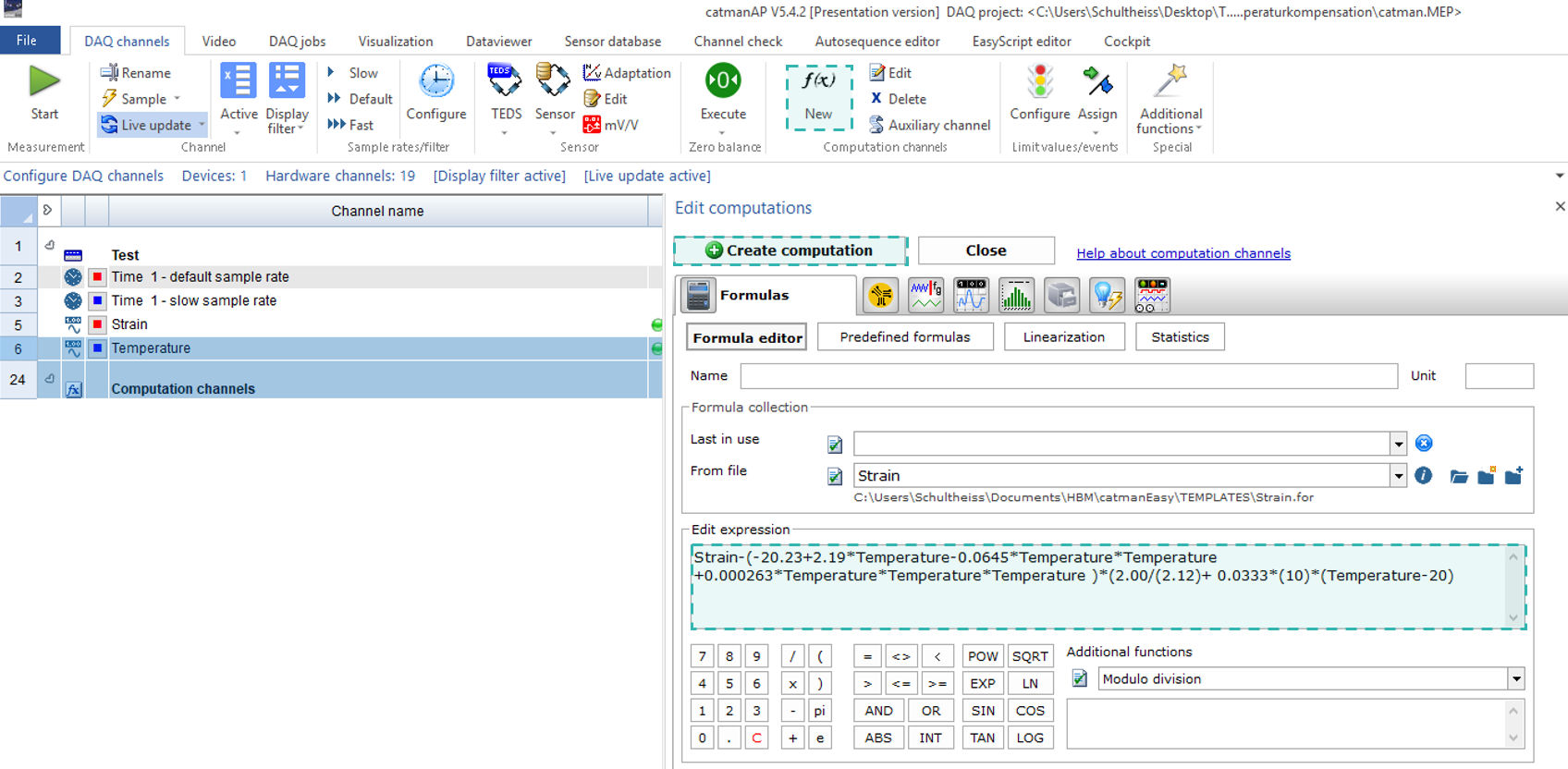
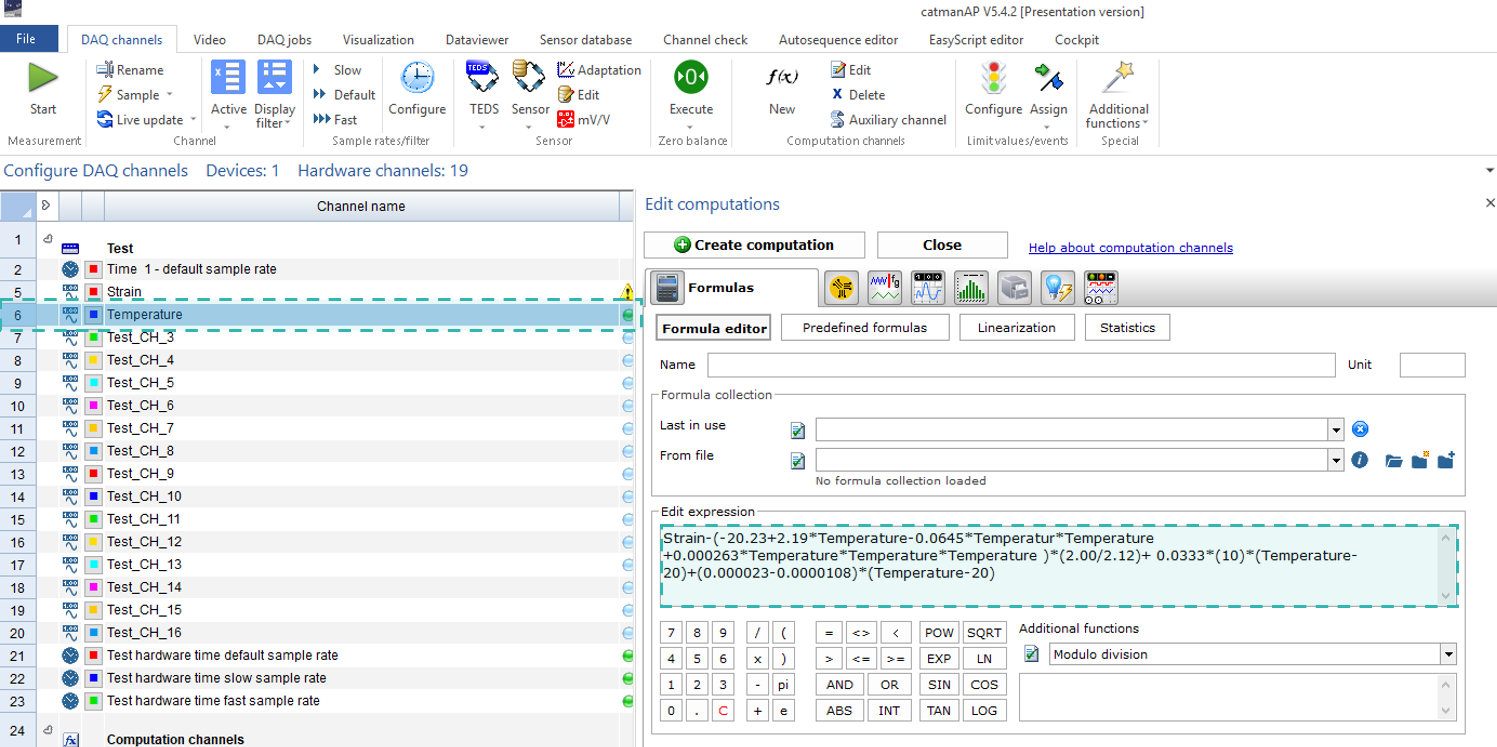
Das angepasste Polynom sieht wie folgt aus:

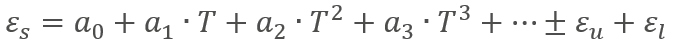
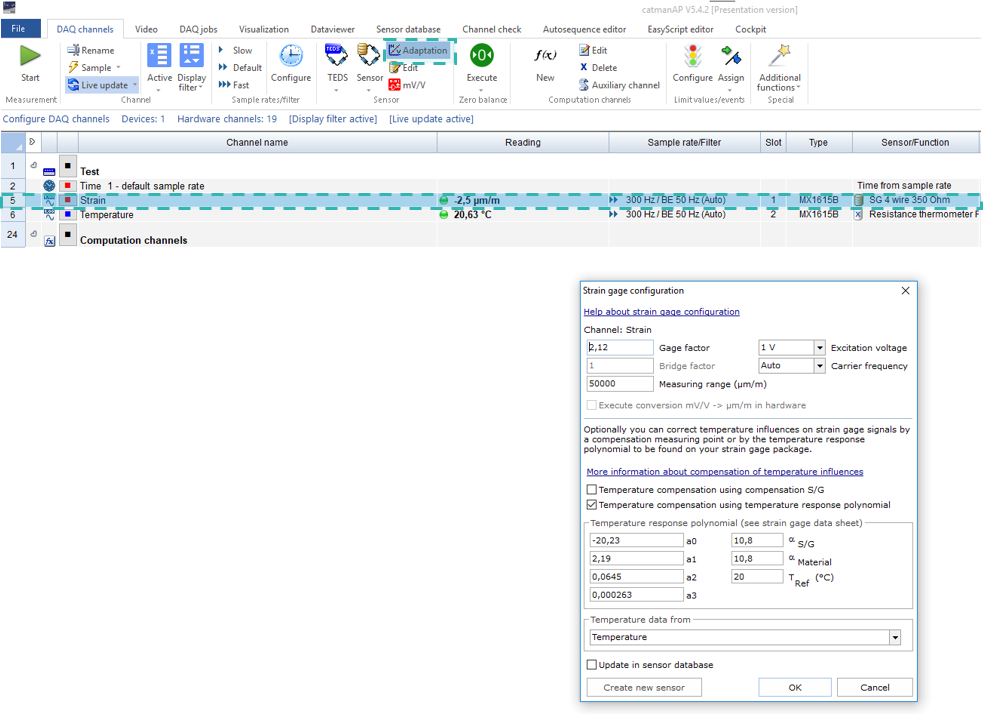
Wenn wir uns auf unser Anwendungsbeispiel konzentrieren, erhalten wir:

Nehmen wir an, dass die Temperatur während der Dehnungsmessung konstant bei 100 °C (T = 100 °C) liegt und die Länge der Anschlussbändchen 10 mm (L = 10 mm) beträgt. Bitte beachten Sie, dass die Länge der Anschlussbändchen variieren kann. Betrachtet man das Polynom, zeigt sich, dass die temperaturbedingte Dehnung einen erheblichen Einfluss auf das Ergebnis hat, da sie größer als 100 μm/m ist!

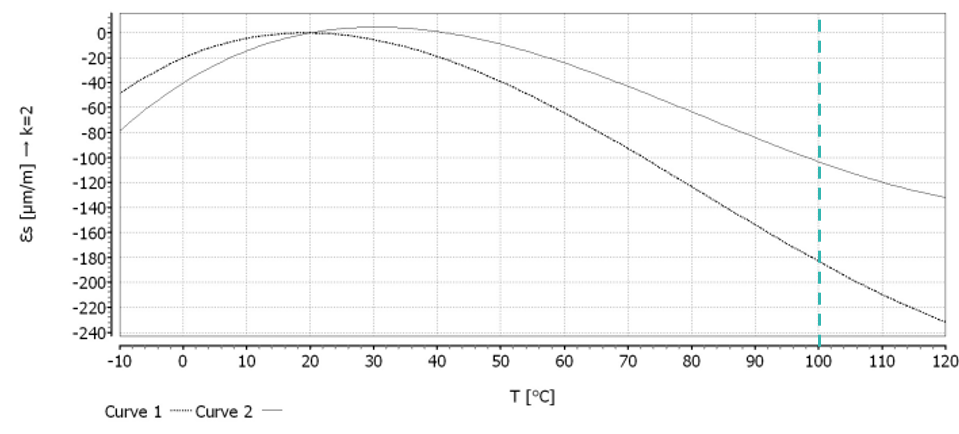
Zur Berechnung der temperaturbedingten Dehnung setzen wir die Temperatur und die Länge der Anschlussbändchen in das Polynom ein:

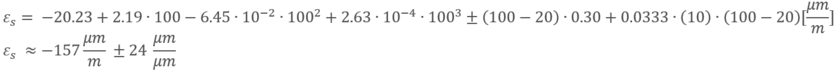
Das Ergebnis passt recht gut zu dem Polynom, das auf dem Datenblatt ausgewiesen ist. Durch Einbeziehung des Polynoms werden die wichtigsten Einflüsse berücksichtigt, während nur sehr lange 2-Leiter-Kabel das Ergebnis zusätzlich beeinflussen können. Da wir die 3- und 4-Leiter-Technik verwenden, die die Auswirkungen des Kabelwiderstands kompensiert, ist dieser Teil der Berechnung nicht relevant!

Die Überlagerung der temperaturbedingten Dehnung auf die gemessene Dehnung ergibt nun den korrigierten Dehnungswert, der nur die mechanische Dehnung berücksichtigt:

Die Polynome der meisten Hersteller werden mit einem festen k-Faktor von k = 2 gemessen, jedoch weicht der real gemessene k-Faktor typischerweise ab. Dieser Effekt zeigt sich vor allem bei extremen Bedingungen wie hohen und niedrigen Temperaturen oder hohen Dehnungen. Zur Korrektur der Schwankungen, die die Temperaturkompensation beeinflussen können, sollte der auf dem Datenblatt angegebene k-Faktor berücksichtigt werden.

Vervielfachen Sie daher den Quotienten der auf dem Datenblatt angegebenen k-Faktoren, um die bei dem DMS zu erwartende temperaturbedingte Dehnung zu kompensieren. In diesem Fall haben wir die folgenden k-Faktoren:

Natürlich wird die Korrektur der temperaturbedingten Dehnung nur auf das Polynom angewendet und darf nicht auf zusätzlich beitragende Faktoren wie Messunsicherheit oder den Einfluss der Anschlussbändchen angewendet werden:

In diesem Fall haben wir zwei k-Faktoren (k_Polynom = 2,0 and k_Datenblatt = 2,12). Die Korrektur der temperaturbedingten Dehnung wäre:

In diesem theoretischen Testfall passt der Temperaturkoeffizient des DMS perfekt zum Werkstoff. Dennoch kann es in der Praxis zu leichten Abweichungen zwischen dem Temperaturkoeffizienten des Substratwerkstoffs und dem Temperaturkoeffizienten kommen, an den der DMS angepasst wurde. Eine ungefähre Anpassung zur Korrektur des gemessenen Dehnungswertes wird durch die folgende Formel gegeben. In diesem Fall gehen wir davon aus, dass ein DMS mit Temperaturganganpassung für ferritischen Stahl (10,8 ppm/K) auf Aluminium (23 ppm/K) verwendet wurde: 

Die Temperaturdifferenz muss aus der Referenztemperatur und der Temperatur während des Tests berechnet werden. Die Referenztemperatur ist die Temperatur, auf die sich das DMS-Datenblatt bezieht und für die die Parameter gemessen wurden:

Dies führt zu folgendem Korrekturfaktor:

In Kapitel 2 erfolgte die Dehnungskorrektur über das Polynom und die Anpassung des k-Faktors. Dies ist für die meisten experimentellen Prüfungen ausreichend. Die Dehnungsempfindlichkeit (k-Faktor) weist jedoch außerdem eine über einen weiten Bereich ungefähr lineare Temperaturabhängigkeit auf. Eine Korrektur des k-Faktors kann daher für das nicht korrigierte Dehnungssignal in Betracht kommen (nicht jedoch für das Polynom, da die Temperaturabhängigkeit des k-Faktors im Polynom bereits berücksichtigt ist). Der Temperaturkoeffizient kann je nach Messgitterwerkstoff positiv oder negativ sein (Konstantan oder CrNi (ModCo).

Zur einfachen Berechnung des um Temperatureinflüsse bereinigten k-Faktors sind im HBK-Datenblatt der Temperaturkoeffizient und der erforderliche k-Faktor angegeben (k_{data_sheet} = 2.12). Bitte prüfen Sie zunächst, ob das lineare Verhalten auch für extreme Temperaturen gilt. In diesem Fall ist der Temperaturkoeffizient des k-Faktors:

Tech Note als PDF herunterladen

Haftungsausschluss: Die TECH NOTES von HBK bieten neben der üblichen Dokumentation einen schnellen Überblick zu einem bestimmten Thema. TECH NOTES werden kontinuierlich verbessert und ändern sich daher häufig. HBM übernimmt keine Haftung für die Vollständigkeit der Beschreibungen. Wir behalten uns das Recht vor, jederzeit und ohne vorherige Ankündigung Änderungen an den Funktionen und/oder Beschreibungen vorzunehmen.