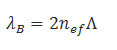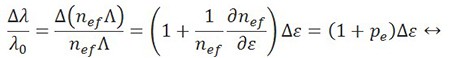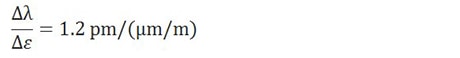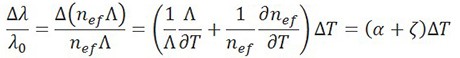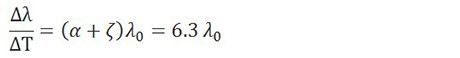Messprinzip eines Faser-Bragg-Gitters
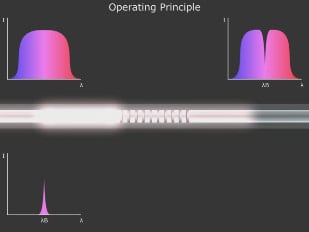
Das Faser-Bragg-Gitter (FBG) ist eine periodische Mikrostruktur, die selektiv Wellenlängen reflektiert. Das bedeutet: wenn Licht von einer Quelle mit großer Bandbreite in den Lichtwellenleiter eingebracht wird, wird am Gitter nur Licht einer sehr begrenzten spektralen Breite um die Bragg-Wellenlänge reflektiert. Die restlichen Anteile des Lichts setzen ihren Weg durch den Lichtwellenleiter ohne Dämpfung bis zum nächsten Bragg-Gitter fort. Das Faser-Bragg-Gitter ist symmetrisch und reflektiert daher Licht immer im Bereich der Bragg-Wellenlänge, egal von welcher Seite das Licht kommt.
Die Bragg-Wellenlänge (λB) ist im Wesentlichen definiert durch die Periode der Mikrostruktur (Gitterperiode) (Λ) und den Brechungsindex des Kerns (nef).
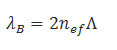
Gleichung 1
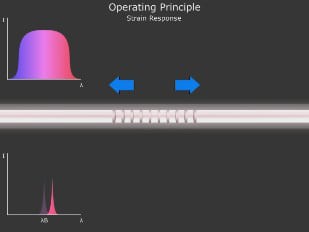
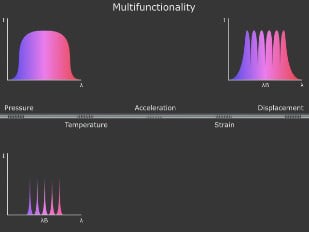
Ein Faser-Bragg-Gitter hat eindeutige Kenndaten, wenn man es als Sensor betrachtet. Streckt oder staucht man zum Beispiel die Faser, misst das FBG Dehnung. Grund dafür ist im Wesentlichen, dass eine Verformung des Lichtwellenleiters eine Veränderung der Gitterperiode und daher der Bragg-Wellenlänge verursacht. Aufgrund des photoelastischen Effekts spielt auch die Änderung des Brechungsindex eine Rolle.
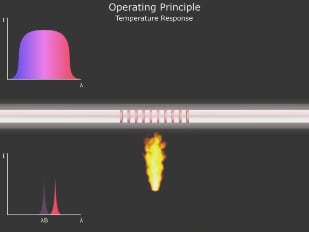
Die Temperaturempfindlichkeit ist ebenfalls ein wesentliches Merkmal von Faser-Bragg-Gittern. In diesem Fall ist die durch den thermooptischen Effekt verursachte Änderung des Brechungsindex des Quarzglases der Hauptfaktor für die Veränderung der Bragg-Wellenlänge. Einen weiteren Beitrag leistet die Wärmeausdehnung, die die Gitterperiode verändert. Dieser Effekt ist jedoch nebensächlich, da Quarzglas nur einen kleinen Wärmeausdehnungskoeffizienten hat.