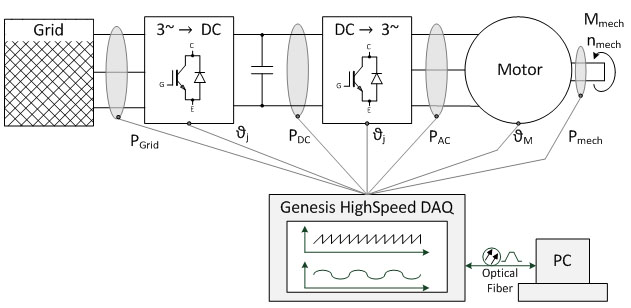
Bei Messungen an energietechnischen Systemen müssen, wie beispielhaft an einem Drehstromantrieb in Bild 1.1 dargestellt, unterschiedliche physikalische Größen erfasst, gespeichert und aufbereitet werden. Genesis HighSpeed Datenrekorder ermöglichen die synchrone Erfassung bei hoher Kanalzahl und hohen Abtastraten von allen wichtigen Größen in energietechnischen Systemen [1]. Speziell bei Systemen, die mit Drehstrom versorgt werden oder ein Drehspannungssystem erzeugen, können die Messgrößen durch die Anwendung von Raumzeigern anschaulich dargestellt und einfach interpretiert werden. Weiterhin können durch die Raumzeigerdarstellung stationäre Betriebszustände sowie dynamische Ausgleichsvorgänge bewertet werden. In diesem Beitrag werden zunächst die Definitionsgleichungen von Raumzeigern sowie die Transformationsvorschriften in unterschiedlichen Koordinatensystemen angegeben. Danach wird die Anwendung der Raumzeiger bei der Darstellung der physikalischen Größen von permanenterregten Synchronmaschinen (PMS) erläutert. Um diese Methoden selbständig zu erproben, wird zu diesem Beitrag eine Perception-Workbench bereitgestellt [3].
Berechnung und Darstellung von Messgrößen in der elektrischen Energietechnik als Raumzeiger mit HBM Perception-Software
Kurzfassung
Um Messgrößen an elektrischen Energieumwandlungssystemen, z. B. Transformatoren oder Drehfeldmaschinen, übersichtlich darzustellen, werden häufig Raumzeiger verwendet. Weitere Informationen über den Betriebszustand dieser Energiewandler können ermittelt werden, wenn die zeitabhängigen Raumzeiger in der komplexen Ebene als Ortskurven dargestellt werden. Eine weitere Vereinfachung zur Darstellung der Messgrößen kann durch die Darstellung der Raumzeiger in rotierenden Koordinatensystemen erreicht werden. In diesem Beitrag wird die Darstellung von Raumzeigern in unterschiedlichen Koordinatensystemen mit der Software Perception am Beispiel der permanenterregten Synchronmaschine erläutert.
1. Einleitung
2. Raumzeiger
Zur Erleichterung der mathematischen Beschreibung von Drehstromsystemen entwickelte K.P. Kovács im Jahr 1959 die Raumzeigertheorie. Diese wird häufig zur Beschreibung von Regelverfahren für Drehfeldmaschinen angewandt [4]. Die elektrischen und magnetischen Größen eines dreiphasigen Drehstromsystems lassen sich auf ein zweiphasiges, orthogonales System und ein unter gewissen Umständen vorhandenes Nullsystem abbilden. Das zweiphasige, orthogonale System lässt sich als komplexe Zahl interpretieren, welche als Raumzeiger bezeichnet wird. Der Realteil und der Imaginärteil der komplexen Zahl entsprechen den Projektionen der, als Zeiger dargestellten, komplexen Zahl auf die Achsen α und β in der komplexen Ebene. In Gleichung 1.01 ist die Berechnungsvorschrift des komplexen Raumzeigers![]() aus den drei Stranggrößen x1, x2 und x3 definiert:
aus den drei Stranggrößen x1, x2 und x3 definiert:
![]()
Hierbei ist α ein komplexer Drehoperator. Das zugehörige Nullsystem wird durch
![]()
berechnet. Bild 2.1a) stellt den Raumzeiger ![]() im orthogonalen Koordinatensystem dar. Der Realteil des Raumzeigers wird auf der Abszisse α und der Imaginärteil auf der Ordinate β aufgetragen. In dieser Darstellung sind die Koordinatenachsen (α, β) ruhend. Die Stranggrößen erhält man durch die Projektion des Raumzeigers auf die um 120° verdrehten Achsen a, b, c.
im orthogonalen Koordinatensystem dar. Der Realteil des Raumzeigers wird auf der Abszisse α und der Imaginärteil auf der Ordinate β aufgetragen. In dieser Darstellung sind die Koordinatenachsen (α, β) ruhend. Die Stranggrößen erhält man durch die Projektion des Raumzeigers auf die um 120° verdrehten Achsen a, b, c.
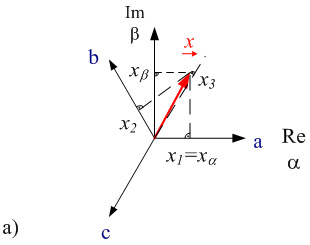
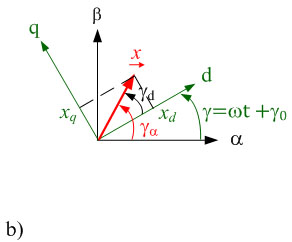
Bild 2.1: Raumzeigerdarstellung in der komplexen Ebene a) in ruhenden α, β und
b) in rotierenden Koordinatensystemen
In der Software Perception werden vordefinierte Funktionen zur Verfügung gestellt, um die Transformationen der dreiphasigen Größen (x1, x2, x3) in Raumzeigergrößen zu ermöglichen:

Ebenso stellt Perception für die Rücktransformation, um aus Raumzeigergrößen die zugehörigen Stranggrößen zu berechnen eine mathematische Funktion zur Verfügung:

Die Bedeutungen der unterschiedlichen Übergabeparameter werden bei der Eingabe der Formeln in Perception in der Online-Hilfe genau beschrieben.
Mit Hilfe dieser Transformations-Funktionen, können nun Berechnungen im Raumzeigerbereich ausgeführt und die Berechnungsergebnisse anschließend wieder als Stranggrößen angezeigt werden.
In vielen Anwendungsfällen kann der Rechenaufwand reduziert und die Anschaulichkeit der gewonnen Ergebnisse verbessert werden, wenn die Raumzeiger in rotierenden Koordinatensystemen dargestellt werden. Bei den bisherigen Betrachtungen war das Koordinatensystem mit den α- und β-Achsen ruhend. Jetzt sollen Raumzeiger zusätzlich in einem d,q-Koordinatensystem betrachtet werden, das gegenüber dem ursprünglichen α,β-Koordinatensystem um einen beliebigen zeitabhängigen Winkel γ(t) gedreht ist. Die Ableitung der Transformationsvorschriften vereinfacht sich, wenn die Raumzeiger in Polardarstellung beschrieben werden. Der Raumzeiger im ruhenden Koordinatensystem lautet in Polardarstellung:
![]()
Nach Bild 1.1b) kann dieser Raumzeiger auch in einem rotierenden Koordinatensystem mit d- und q-Achsen beschrieben werden. Das hochgestellte R kennzeichnet, dass der Raumzeiger in rotierenden Koordinatensystemen dargestellt wird. In der Polardarstellung ändert sich in unterschiedlichen Koordinatensystemen der Betrag nicht, lediglich der Winkel muss angepasst werden.
![]()
Die Transformation der Raumzeiger von einem in ein anderes Koordinatensystem erfolgt über die Multiplikation mit dem Drehoperator ejγ.
![]()
Mithilfe der Eulersche Formel ejγ = cos(γ)+j sin(γ)können die Komponenten des rotierenden Raumzeigers berechnet werden.
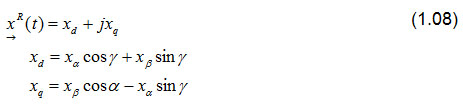
Für die Transformation der drei Stranggrößen x1, x2 und x3 in einen rotierenden Raumzeiger stellt Perception die Funktionen
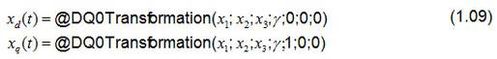
zur Verfügung. Der für die Transformation notwendige Winkel γ wird je nach Anwendung entweder berechnet oder über einen Lagegeber eingelesen.
3. Permanenterregte Synchronmaschine
Die Anwendung der Raumzeiger in unterschiedlichen Koordinaten soll am Beispiel einer permanenterregten Synchronmaschine erläutert werden [4]. Um die Beschreibung der Maschine einfach zu halten, wird dazu eine isotrope Synchronmaschine betrachtet. D.h. das Magnetfeld kann sich richtungsunabhängig in der Maschine ausdehnen. In Bild 3.1a) ist eine PSM mit aufgeklebten Permanentmagneten dargestellt. Dieser Maschinentyp kann in guter Näherung als isotrop betrachtet werden. Die dargestellte Maschine besitzt eine Polpaarzahl von p=2. Um eine allgemein verwendbare Beschreibung der Maschinen zu erhalten, werden die realen Maschinen mit Modellen, mit einer Polpaarzahl von p=1, beschrieben. Zur weiteren Beschreibung soll das einfache Raumzeigermodell der PSM in Bild 3.1b verwendet werden. Dazu muss der Zusammenhang zwischen der mechanischen Drehzahl n und der elektrischen Frequenz fmit

berücksichtigt werden.

Bild 3.1: a) Prinzipieller Aufbau einer PSM und b) Raumzeiger-Modell einer PSM
Ist an der Welle der Synchronmaschine ein Lagegeber angebracht, kann über die Polpaarzahl p und einen Offset- Winkel γ0 der für die Raumzeiger-Transformation notwendige Winkel γ berechnet werden. Dazu wird die in Perception definierte Funktion
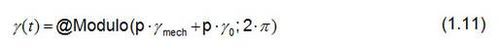
verwendet. Der Offset-Winkel γ0 berücksichtigt den mechanischen Versatz zwischen dem Nordpol des Rotors und der Nulllage des Lagegebers.
Um den Offset-Winkel γ0 zu bestimmen, kann ein Leerlaufversuch genutzt werden. Dazu wird die Synchronmaschine über die Welle mechanisch angetrieben. In Bild 3.2 sind der zeitliche Verlauf der Sternspannung und der von einem Lagegeber eingelesene mechanische Winkel γmech dargestellt. Aus der zeitlichen Verschiebung zwischen dem Nulldurchgang mit negativer Steigung der Spannung u1 und der Nullposition des Lagegebers kann der Offset-Winkel γ0 abgelesen werden.
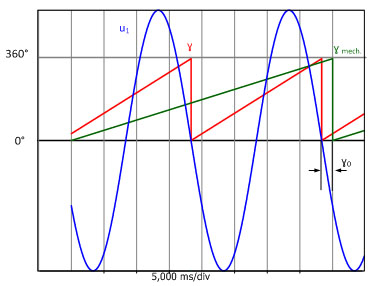
Bild 3.2: Zeitlicher Verlauf der Sternspannung u1, des mechanischen Winkels γmech und des elektrischen Winkels γ.
Die im Leerlaufversuch induzierten Sternspannungen sind in Bild 3.3 dargestellt. Diese drei sinusförmigen Spannungen bilden ein symmetrisches Drehspannungssystem, wenn die Amplituden der Spannungen gleich groß sind und die Phasenverschiebung zwischen den Spannungen 120° beträgt. Die zu dieser Drehspannung zugehörigen Raumzeiger-Komponenten (uα,uβ) sind ebenfalls in Bild 3.3a als Funktion der Zeit dargestellt. Zwischen den Raumzeiger-Komponenten (uα,uβ) stellt sich bei einem symmetrischen Spannungssystem eine Phasenverschiebung von 90° ein.
Werden die Raumzeiger-Komponenten in einem xy-Plot dargestellt, durchläuft die Spitze des Spannungsraumzeigers – wie in Bild 3.3b dargestellt – eine Kreisbahn. Weicht die Bahnkurve des Raumzeigers von der idealen Kreisbahn ab, so ist mit einem Blick ersichtlich, dass die drei Spannungen kein symmetrisches Drehspannungssystem bilden.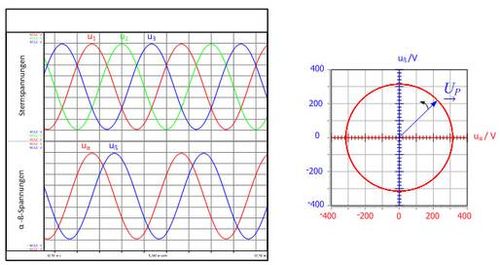 b)
b)
Bild 3.3: a) Zeitlicher Verlauf der Sternspannungen u1, u2 und u3 sowie der Raumzei-gerkomponenten (uα,uβ) b) Bahnkurve des Spannungs-Raumzeigers
Werden nun die Raumspannungszeiger mit den Komponenten uαund uβ in einem rotierenden Koordinatensystem mit den Komponenten ud und uq dargestellt, so werden aus diesen zeitlich veränderlichen Größen konstante Größen. Die Komponenten ud und uq eines symmetrischen Drehspannungssystems sind in Bild 3.4einmal als Zeitverlauf undeinmal als Zeiger in der komplexen Ebene dargestellt. Ein symmetrisches Drehspannungssystem wird in der komplexen Ebene als ruhender Zeiger mit konstanter Länge dargestellt.
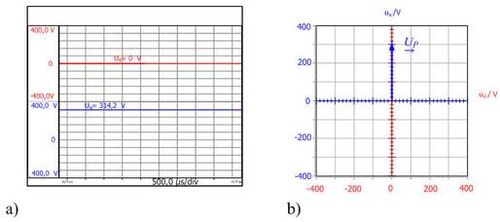
Bild 3.4: a) Zeitlicher Verlauf der Spannungs-Raumzeigerkomponenten ud und uq
b) Spannungs-Raumzeigers im rotierenden Koordinatensystem
Zusammenfassung
In diesem Bericht wird die Signalaufbereitung mit einem Genesis HighSpeed Datenrekorder und der Software Perception mit Hilfe der Raumzeigerrechnung vorgestellt. Es werden die Transformationsvorschriften angegeben, um aus den Rohdaten eines Genesis HighSpeed Datenrekorders die Raumzeiger in unterschiedlichen Koordinatensystemen zu berechnen. Diese werden am Beispiel des Leerlaufversuches mit einer Synchronmaschine mit unterschiedlichen Darstellungsmethoden der Raumzeiger unter Perception erläutert und vorgeführt. Zur weiteren praktischen Erprobung der Berechnungsmethoden mit Raumzeigern in der Energietechnik stellt HBM eine Workbench unter Perception zur Verfügung [3].
Literaturverzeichnis
[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft; Tagungsband 3. Tagung Innovation Messtechnik; 14. Mai 2013
[2] Berechnung von Leistungsgrößen mit Perception-Software
https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/
[3] www.hbm.com
[4] J. Teigelkötter: Energieeffiziente elektrische Antriebe, 1. Auflage, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3