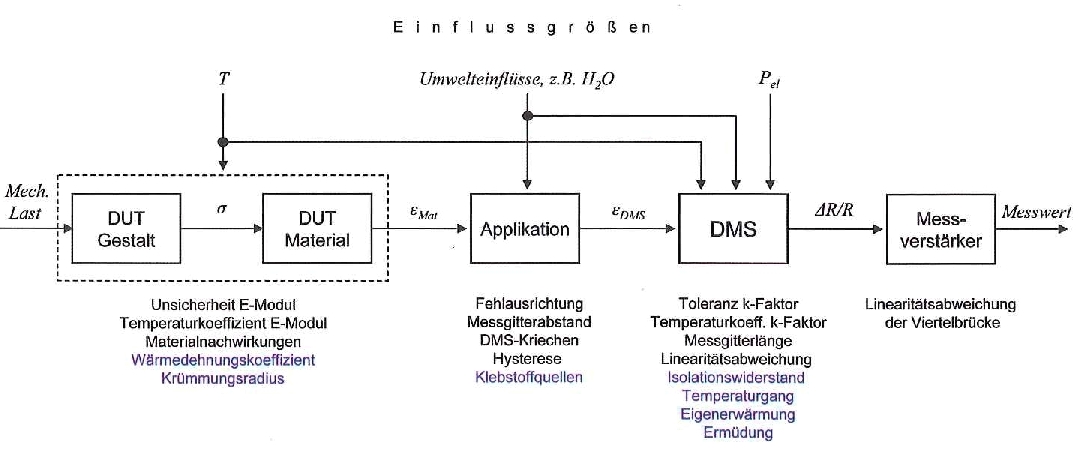
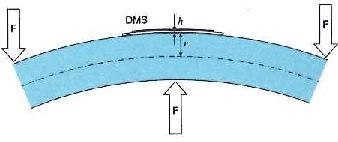
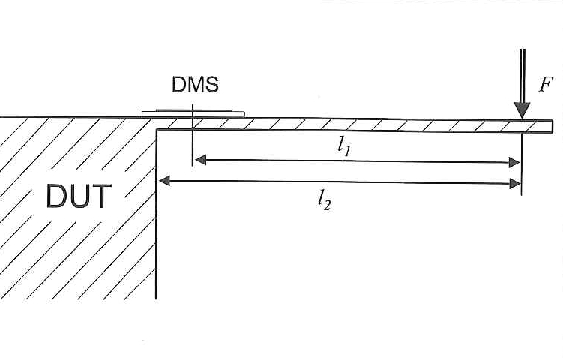
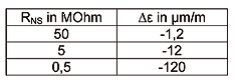
Linearitätsabweichung der Viertelbrücke
Es ist üblich, kleine relative Widerstandsänderungen mit der Wheatstone- Brücke auszuwerten. In der ESA wird, wie bereits ausgeführt, meist nur ein Dehnungsmessstreifen je Messstelle verwendet. Die weiteren Brückenwiderstände sind damit dehnungsunabhängig. Die korrekte Beziehung für das Spannungsverhältnis lautet in diesem Fall:

Obgleich der Zusammenhang nichtlinear ist, wird in der messtechnischen Praxis (bewusst oder auch unbewusst) Linearität unterstellt und die Näherungsgleichung

benutzt. Die relative Abweichung, hervorgerufen durch diese Vereinfachung, kann mit Gl.

berechnet werden. Aus einer Dehnung von 1000 μm/m resultiert (mit k = 2) eine relative Widerstandsänderung von 0,2 %.
Die relative Messabweichung ergibt sich mit Gl. 17 zu -0,1 %. Das entspricht einer absoluten Abweichung von -1 μm/m. Diese Abweichung vom wahren Wert ist vernachlässigbar.
Jedoch treten bei höheren Dehnungen nennenswerte Linearitätsabweichungen auf, wie oben bereits erwähnt:
10.000 μm/m erzeugen eine Abweichung von -1 %,
100.000 μm/m erzeugen eine Abweichung von -9,1 %.
Bei Verwendung von Konstantan-Dehnungsmessstreifen (Nichtlinearität betragsmäßig ähnlich, jedoch gegensätzliches Vorzeichen) heben sich beide Abweichungen weitestgehend auf und sollen deshalb nicht weiter berücksichtigt werden.
Man beachte aber, dass keine Kompensation vollständig gelingt, zumal der k-Faktor etwas von 2 abweicht und die tatsächliche statische Kennlinie nicht exakt der empirischen Gl. 12 entspricht.