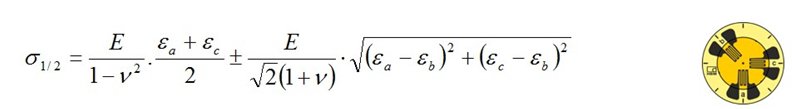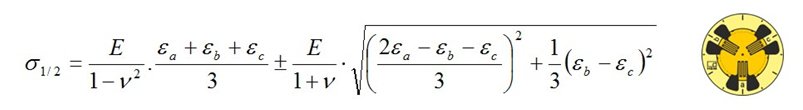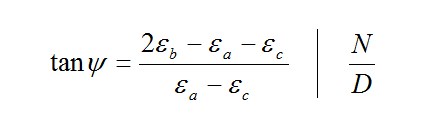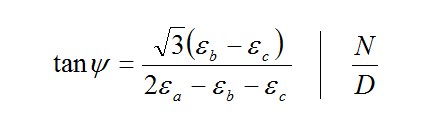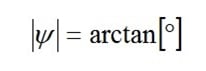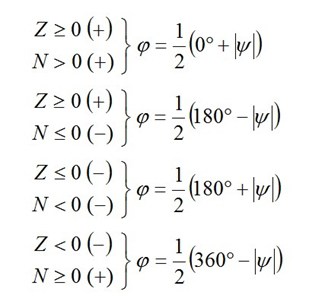Bestimmung von Werkstoffspannungen aus Dehnungsmessungen
Im elastischen Verformungsbereich eines Werkstoffs beruhen die Methoden zur Berechnung der Werkstoffspannungen aus den gemessenen Dehnungen auf dem Hookeschen Gesetz. In seiner einfachsten Form lautet das Hookesche Gesetz:
σ = ε Ε
σ = Werkstoffspannung [N/mm2]
ε = Dehnung [µm/m]
Ε = Elastizitätsmodul [N/mm2]
Diese Variante des Hookeschen Gesetzes gilt nur für den einachsigen Spannungszustand. Zweiachsige und mehrachsige Spannungszustände erfordern erweiterte Varianten.
Anmerkung: Bei Dehnungsmessungen kann immer nur der Unterschied zwischen einem bestehenden Ausgangszustand und einem später eintretenden, veränderten Zustand bestimmt werden. Der Ausgangszustand kann ein lastfreier Zustand sein, er kann aber auch ein Zustand erheblicher Vorbelastung sein, beispielsweise durch das Eigengewicht des Objekts (z.B. einer Brücke).
Vorbelastungen oder auch Eigenspannungszustände lassen sich nur dann messen, wenn ein Eingriff in das Objekt erlaubt ist, z.B. das Anbringen einer kleinen Bohrung.
Die Werkstoffspannung σ darf nur dann nach dem Hookeschen Gesetz für den einachsigen Spannungszustand nach der unten stehenden Gleichung berechnet werden, wenn die Dehnung ε in der Kraftwirkungsrichtung (0°-Richtung) gemessen wurde.
In der Querrichtung (90°-Richtung) ist trotz der messbaren Dehnung (Querkontraktion, Querdilatation) keine Werkstoffspannung vorhanden.
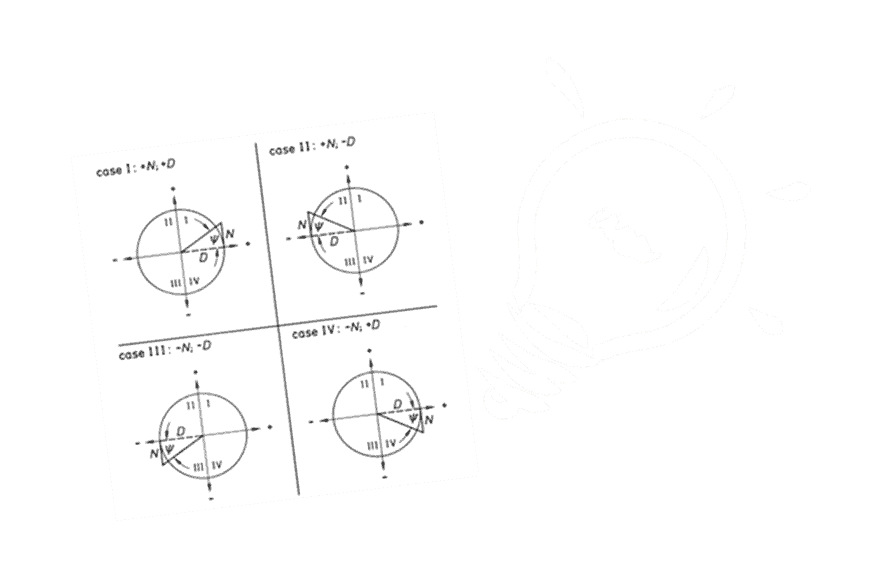
Man muss also, will man zu verlässlichen Ergebnissen kommen, die Kraftwirkungsrichtung kennen und in dieser Richtung die Dehnung messen. Ist diese Richtung nicht oder nur näherungsweise bekannt, dann sind Messungen und deren Auswertung wie beim zweiachsigen Spannungszustand mit unbekannten Hauptrichtungen auszuführen.
Im Aufgabengebiet der experimentellen Spannungsanalyse dürfte der einachsige Spannungszustand eher einen Ausnahmefall darstellen. Weitaus häufiger wird man den zweiachsigen Spannungszustand antreffen, dessen Ermittlung nicht mehr in der für den einachsigen Spannungszustand zutreffenden, einfachen Weise vorgenommen werden darf; dies würde zu beträchtlichen Fehlern führen.
Beim ebenen Spannungszustand treten die extremen Normalspannungen σ1 und σ2 in den rechtwinklig aufeinander stehenden Richtungen 1 und 2 auf. Man nennt die Spannungen σ1 und σ2 die Hauptspannungen und analog die Richtungen 1 und 2 die Hauptrichtungen des ebenen Spannungsfeldes. Sind die Hauptnormalspannungen und ihre Wirkungsrichtungen bekannt, dann ist der zweiachsige Spannungszustand eindeutig definiert.
Bekannte Hauptspannungsrichtungen findet man z.B. an der Oberfläche eines kreiszylindrischen Behälters unter Innendruck, an einer mit reiner Torsion beanspruchten Welle und im randzonenfreien Bereich einer gebogenen Platte.
Bei anderen Objekten und bei gleichzeitiger Einwirkung verschiedener Einflussgrößen, wie beispielsweise Normalkraft und Biegung oder Torsion und Biegung oder dergleichen müssen die Hauptrichtungen als nicht bekannt vorausgesetzt werden.
Die Hauptnormalspannungen σ1 und σ2 des zweiachsigen ebenen Spannungszustandes errechnen sich nach dem erweiterten Hookeschen Gesetz aus den gemessenen Hauptdehnungen ε1 und ε2, dem Elastizitätsmodul E des Werkstoffs und der Querzahl v des Werkstoffs zu:
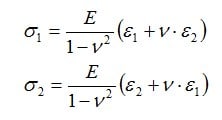
Es wird vorausgesetzt, dass die Spannung σ3 in der 3. Hauptrichtung (senkrecht zur Oberfläche) gleich Null ist.
Zur Verminderung des Installationsaufwands eignen sich für Messungen im zweiachsigen Spannungsfeld mit bekannten Hauptrichtungen insbesondere X-Rosetten. Die Achsen der beiden Messgitter müssen übereinstimmend mit den Achsen der Hauptnormalspannungen (Hauptdehnungsrichtungen) sein.
Bei komplizierter gestalteten Objekten, bei Überlagerung verschiedener Beanspruchungsarten (Normal-, Biege- oder Torsionsbeanspruchung) oder an Störstellen (z.B. Querschnittsänderungen) ist eine Voraussage der Hauptspannungsrichtungen in aller Regel nicht möglich.
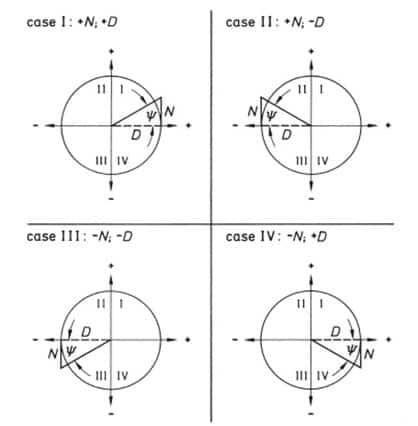
In jedem Fall, in dem die Hauptspannungsrichtungen nicht eindeutig feststehen, muss die Spannungsanalyse nach der weiter unten beschriebenen Methode durchgeführt werden.