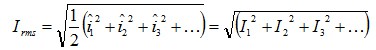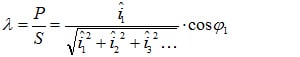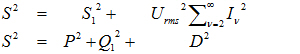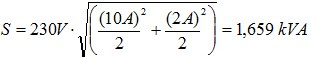Introduction
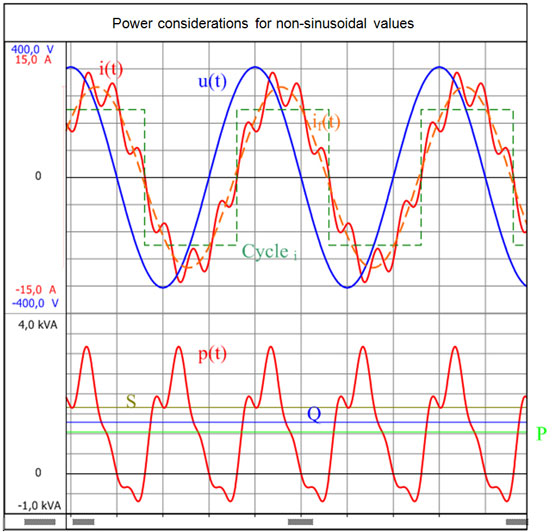
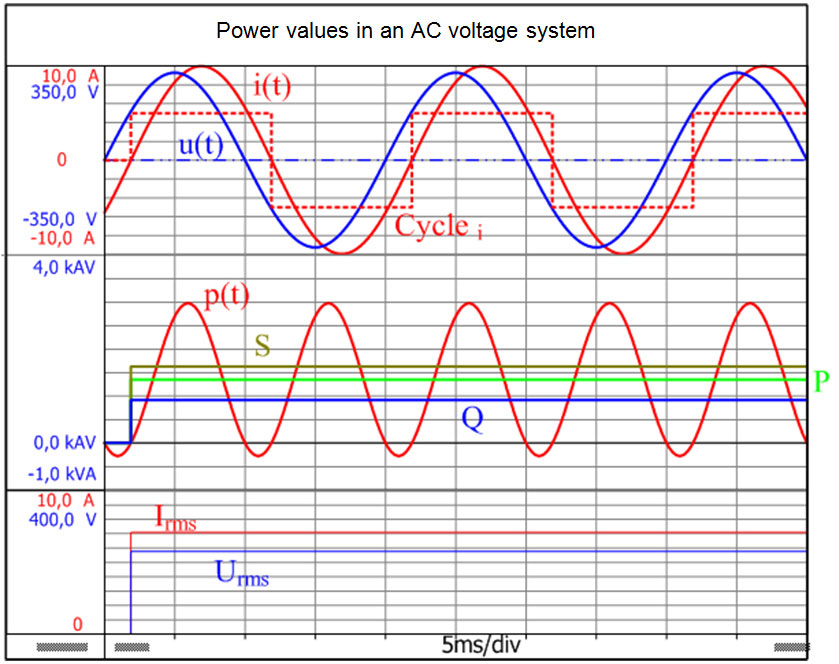
Electrical machines convert electrical energy and mechanical energy. The direction of energy flow is identified by the designation of the mode in which the machine is operating. In motor mode, electrical energy is converted into mechanical energy. In generator mode, the electrical machine is driven and converts mechanical energy into electrical energy. Energy converters are identified by the energy converted per unit of time, rather than simply by the energy that is converted. This value is called instantaneous power, or p(t).
![]()
(1.01)
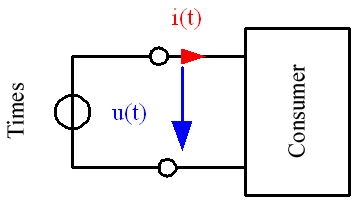
Fig 1.1 shows a two-wire network with an energy source and the corresponding consumer. The applied voltage u(t) and consumer current i(t) can be measured at the measurement points. The instantaneous power is derived from the product of these variables:
![]()
(1.02)
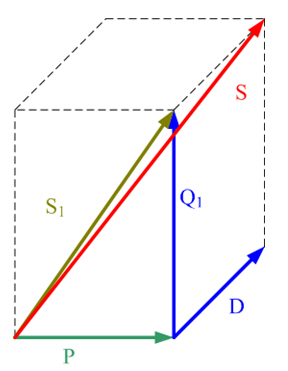
The system of consumer count arrows used in Fig. 1.1 shows how the consumer absorbs power when the instantaneous power is positive (p(t) >0). If the instantaneous power is negative (p(t) <0), the consumer feeds power into the source.
The mean value of the instantaneous power p(t) over the duration of the cycle T is referred to in electrical engineering as the effective power P.
![]()
(1.03)
The process for determining active, reactive and apparent power from measured current and voltage curves with Perception is described below.
The implementation of formula (1.03) in Perception software is shown by the example of the extract from the Perception formula database (1.04).

(1.04)

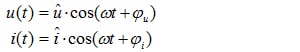
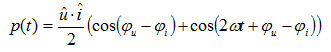
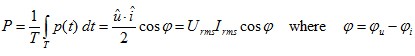 (2.03)
(2.03)
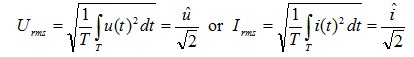
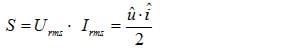 (2.05)
(2.05)