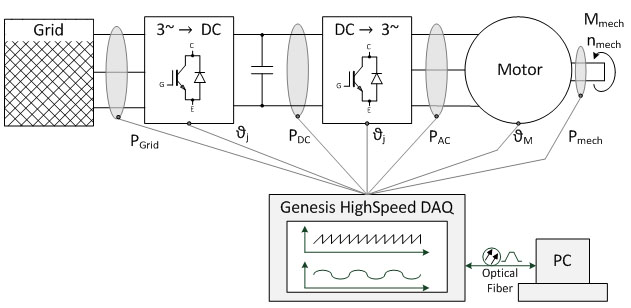
Cuando se realizan mediciones en sistemas eléctricos es preciso registrar, guardar y acondicionar diversas magnitudes físicas, como se ilustra en la figura 1.1 para un sistema de accionamiento trifásico. Los registradores de datos Genesis HighSpeed permiten adquirir de forma sincronizada todas las magnitudes importantes de un sistema eléctrico, con un gran número de canales y altas frecuencias de muestreo [1]. El uso de vectores espaciales para representar las magnitudes medidas permite obtener una imagen más clara y fácil de interpretar, sobre todo en sistemas que se alimentan con corriente trifásica o cuando se construye un sistema trifásico. Los vectores espaciales también se pueden utilizar para representar estados de funcionamiento estacionarios y transitorios. En este artículo se explican en primer lugar las ecuaciones que definen los vectores espaciales y las reglas de transformación en los distintos sistemas de coordenadas. A continuación se explica cómo utilizar los vectores espaciales para representar magnitudes físicas de equipos sincrónicos con excitación permanente (PSM). Existe un workbench de Perception [3] para probar de manera independiente los distintos métodos.
Cálculo y representación de magnitudes medidas eléctricas como vectores espaciales mediante el software Perception de HBM
Resumen
Los vectores espaciales se utilizan con frecuencia para representar de forma clara y concisa magnitudes medidas en sistemas de conversión de energía eléctrica, como transformadores o motores de inducción. Cuando estos vectores espaciales dependientes del tiempo se representan en el plano complejo, es posible obtener información adicional relativa al estado de funcionamiento de estos convertidores de energía. Para simplificar todavía más la representación de estas magnitudes medidas, los vectores espaciales se pueden referenciar a sistemas de coordenadas giratorios. Este artículo explica cómo representar vectores espaciales en distintos sistemas de coordenadas con el software Perception, tomando como ejemplo una máquina síncrona con excitación permanente.
1. Introducción
2. Vectores espaciales
La teoría de los vectores espaciales fue desarrollada por K. P. Kovacs en 1959 con el fin de facilitar la descripción matemática de los sistemas trifásicos. Se utiliza con frecuencia para describir métodos de control para motores de inducción [4]. Las magnitudes eléctricas y magnéticas de un sistema trifásico se pueden caracterizar mediante un sistema ortogonal bifásico y un sistema de secuencia cero (que solo está presente en determinadas circunstancias). El sistema ortogonal bifásico se puede interpretar como un número complejo, que se denomina vector espacial. Sus partes real e imaginaria se corresponden con las proyecciones del número complejo, representadas como un vector, sobre los ejes α y β del plano complejo. La ecuación 1.01 define las reglas de cálculo del vector espacial complejo
![]() a partir de las tres variables de la línea x1, x2 y x3:
a partir de las tres variables de la línea x1, x2 y x3:
![]()
α es un operador de rotación complejo. El sistema de secuencia cero correspondiente se calcula mediante
![]()
La figura 2.1a) muestra el vector espacial ![]() en un sistema de coordenadas ortogonal.
en un sistema de coordenadas ortogonal.
La parte real del vector espacial aparece en el eje de abscisas α y la parte imaginaria en el de ordenadas β. En esta figura, los ejes de coordenadas (α, β) se encuentran en reposo. Las magnitudes de las fases de la línea se pueden obtener proyectando los vectores espaciales sobre los ejes a, b, c, con un desfase de 120°.
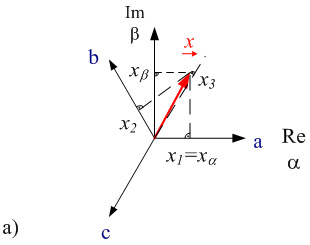
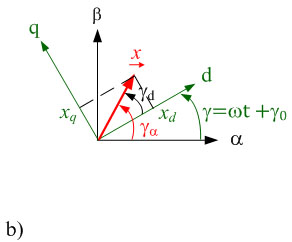
Fig. 2.1: Representación de vectores espaciales en el plano complejo a) en un sistema de coordenadas α, β en reposo y b) en un sistema de coordenadas giratorio
El software Perception ofrece funciones predefinidas para transformar magnitudes trifásicas (x1, x2, x3) en magnitudes de vectores espaciales:

Perception también dispone de una función matemática para la transformación inversa, que permite calcular magnitudes de línea a partir de magnitudes de vectores espaciales:

El significado de los distintos parámetros de transferencia se describe claramente en la ayuda en línea, disponible cuando se introducen las fórmulas en Perception.
La representación de los vectores espaciales como sistemas de coordenadas giratorios permite reducir el volumen de computación para muchas aplicaciones, al tiempo que aumenta la calidad de los resultados obtenidos. Hasta ahora hemos hablado de sistemas de coordenadas con los ejes α y β estacionarios. Ahora, también veremos vectores espaciales en un sistema de coordenadas d,q que rota cualquier ángulo dependiente del tiempo γ(t) con respecto al sistema de coordenadas α,β original. El cálculo de las reglas de transformación se simplifica si los vectores espaciales representan en coordenadas polares. En notación polar, el vector espacial en el sistema de coordenadas en reposo se describe del modo siguiente:
![]()
Como se muestra en la figura 1.1b), este vector espacial también se puede describir en un sistema de coordenadas giratorio con ejes d y q. El superíndice R indica que el vector espacial se representa empleando sistemas de coordenadas giratorios. En una representación polar, la cantidad no varía de un sistema de coordenadas a otro. Únicamente es preciso ajustar el ángulo.
![]()
Los vectores espaciales se transforman de un sistema de coordenadas a otro multiplicándolos por el operador de rotación ejγ.
![]()
Para calcular los componentes del vector espacial giratorio, se puede utilizar la fórmula de Euler ejγ = cos(γ)+j sin(γ).
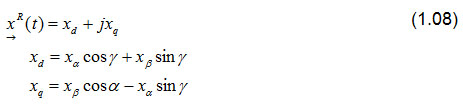
Perception ofrece estas funciones para transformar las tres magnitudes de línea x1, x2 y x3en un vector espacial rotatorio.
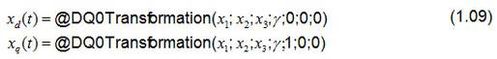
Un codificador de posición calcula o lee el ángulo γ necesario para la transformación, en función de la aplicación.
3. Máquina sincrónica con excitación permanente
El uso de vectores espaciales en diferentes sistemas de coordenadas se explica utilizando como ejemplo una máquina sincrónica con excitación permanente [4]. Para que la descripción de la máquina resulte sencilla, tomamos como referencia una máquina sincrónica isótropa (es decir, que el campo magnético actúa en la máquina del mismo modo en todas direcciones). La figura 3.1a) muestra un motor sincrónico de imanes permanentes (PMSM) para montaje superficial. Este tipo de máquina se puede considerar aproximadamente isótropa. El número de pares de polos de la máquina que se considera es p=2, pero para obtener una descripción de las máquinas que se pueda utilizar de manera amplia, se considera un número de pares de polosp=1. Como base para nuestra descripción, utilizamos el modelo de vector espacial sencillo del PSM de la figura 3.1b). Para ello, debemos tener en cuenta la correlación entre la velocidad mecánica n y la frecuencia eléctricaf, donde

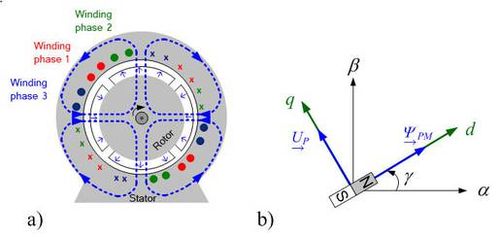
Figura 3.1: a) Diseño básico de un PSM b) Modelo de vector espacial de un PSM
Si se sitúa un codificador de posición en el eje de la máquina sincrónica, es posible calcular el número de pares de polos p y el ángulo de desplazamiento γ0 del ángulo γ, necesario para la transformación del vector espacial. La función
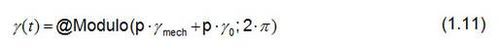
se define en Perception y se utiliza con este fin. El ángulo de desplazamiento γ0 tiene en cuenta el desplazamiento mecánico entre el polo norte del rotor y la posición cero del codificador de posición.
Se utiliza una prueba sin carga para determinar el ángulo de desplazamiento γ0. Para ello, el eje acciona mecánicamente la máquina sincrónica. La figura 3.2 muestra la tensión de estrella u1 en función del tiempo y el ángulo mecánico γmech leído por el codificador de posición. El ángulo de desplazamiento γ0 se puede leer a partir del desfase de tiempo entre el cruce por el cero con pendiente negativa de la tensión u1 y la posición cero del codificador de posición.
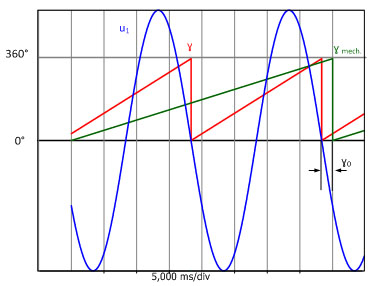
Fig. 3.2: Curva dependiente del tiempo de la tensión de estrella u1, ángulo mecánico γmech y ángulo eléctrico γ
Las tensiones de estrella inducidas en la prueba sin carga aparecen en la figura 3.3. Estas tres tensiones sinusoidales conforman un sistema trifásico simétrico, a condición de que las amplitudes de las tensiones sean iguales en magnitud y el desplazamiento de fase entre las tensiones sea de 120°. Los componentes del vector espacial (uα,uβ) pertenecientes a esta tensión trifásica también aparecen en la figura 3.3a) en función del tiempo. Dado un sistema de tensión simétrico, se establece una desviación de fase de 90° entre los componentes del vector espacial (uα,uβ).
Si los componentes del vector espacial se representan en un gráfico xy, el pico del vector espacial de tensión describirá un círculo, como se muestra en la figura 3.3b). Si la trayectoria de la curva se desvía de un círculo perfecto, se puede detectar rápidamente que las tres tensiones no forman un sistema trifásico simétrico.
a)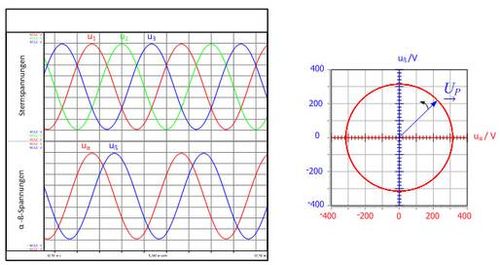 b)
b)
Fig. 3.3: Curva dependiente del tiempo de las tensiones de estrella u1,u2 y u3 de los componentes del vector espacial uα,uβ (a). Trayectoria del vector espacial de tensión (b)
Ahora, si los componentes del vector espacial de tensión uα y uβ se muestran en un sistema de coordenadas giratorio con componentes ud y uq, estas magnitudes, que varían con el tiempo, se vuelven constantes. Las componentes ud y uqde un sistema trifásico simétrico se muestran en la figura 3.4, primero en función del tiempo y después en el plano complejo. El sistema trifásico asimétrico se representa en el plano complejo como un vector fijo con una longitud constante.
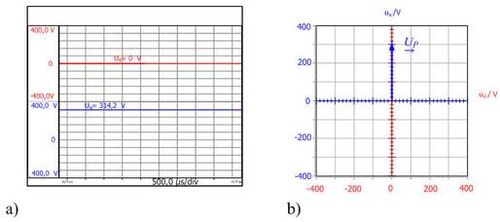
Fig. 3.4: Curva dependiente del tiempo a) de los componentes del vector espacial de tensión ud y uq y
b) del vector espacial de tensión en el sistema de coordenadas giratorio
Conclusión
Este artículo explica el acondicionamiento de la señal con un registrador de datos Genesis HighSpeed y el software Perception, utilizando cálculos de vectores espaciales. Se han descrito las reglas de transformación para el cálculo de vectores espaciales en distintos sistemas de coordenadas a partir de datos en bruto procedentes de un registrador Genesis HighSpeed. Los sistemas de coordenadas se han presentado y explicado tomando como ejemplo una prueba sin carga con una máquina sincrónica. Perception ofrece distintos métodos de visualización de los vectores espaciales. Para realizar pruebas prácticas adicionales de los métodos de cálculo con vectores espaciales eléctricos, HBM ofrece un workbench que se ejecuta en Perception [3].
Bibliografía
[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft [Electromovilidad por la vía rápida: mayor eficiencia para los sistemas de accionamiento del futuro]; actas de la 3.ª conferencia de Innovation Messtechnik [Innovación en las tecnologías de medición]; 14 de mayo de 2013
[2] Berechnung von Leistungsgrößen mit Perception-Software
[Cálculo de valores de potencia con el software Perception] https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/
[3] www.hbm.com
[4] J. Teigelkötter: Energieeffiziente elektrische Antriebe [Sistemas de accionamiento eléctricos energéticamente eficientes], 1.ª edición, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3