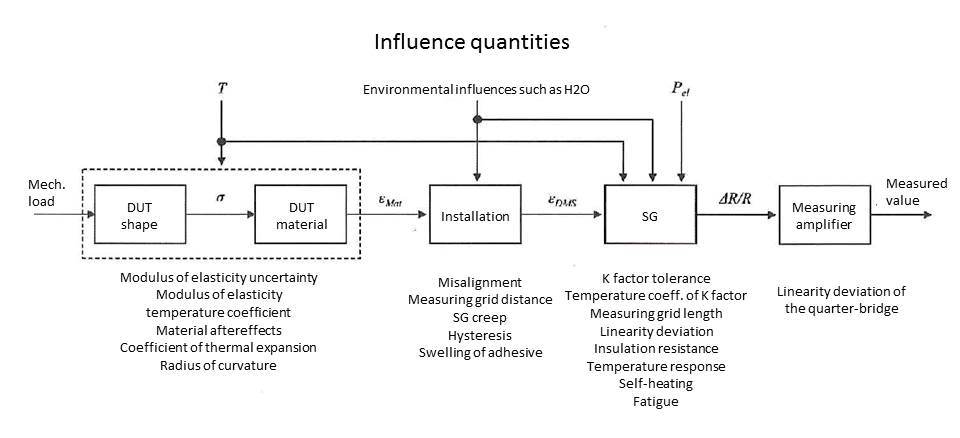
Estimación de la incertidumbre de medida en mediciones referidas al punto cero
Las mediciones en las que el punto cero es importante suelen consistir en medidas a largo plazo en edificios y pruebas de fatiga de componentes. Si, en el curso de una tarea de medición de este tipo, el punto cero cambia, se produce un error de medición adicional. Todas las incertidumbres de medida de las que ya hemos hablado se suman a las que discutimos en esta sección.
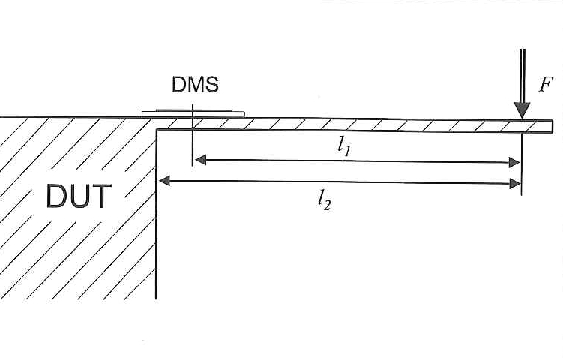
Dilatación térmica del componente, respuesta de temperatura de la galga extensométrica
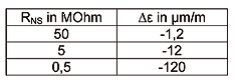
El material del componente tiene un coeficiente de dilatación térmica determinado. Esta dilatación térmica no se mide, sino que es simplemente el resultado de la temperatura, entendida como una magnitud que ejerce una influencia. Por su parte, la rejilla de medición también tiene un coeficiente de dilatación térmica, así como un coeficiente de temperatura que influye en la resistencia eléctrica. Como en el análisis experimental de tensiones solo tienen interés las deformaciones inducidas por la carga, las galgas extensométricas que se ofrecen ya están adaptadas a la dilatación térmica de materiales concretos. No obstante, todos esos coeficientes de temperatura dependen a su vez de la temperatura; en otras palabras, la compensación nunca es perfecta. Siempre habrá una desviación residual ΔƐ que se puede calcular mediante un polinomio. Los coeficientes de dicho polinomio se determinan de forma específica para cada lote y el fabricante los indica en el embalaje de la galga extensométrica.
Aquí puede verse un ejemplo para una galga extensométrica (HBM tipo LY-6/120).
La temperatura se expresa en °C (aunque sin dimensiones) y la desviación residual (deformación aparente) se determina en μm/m. Para una temperatura de 30 °C, la deformación aparente resultante es de -4,4 μm/m.
Si la temperatura ambiente se aleja más de la temperatura de referencia (20 °C) o si la galga extensométrica no se ajusta de forma correcta, las desviaciones serán mucho mayores. Estas desviaciones son de carácter sistémico y pueden eliminarse por medio de cálculos (durante la propia medición). Por otro lado, la ecuación ya exhibe una incertidumbre que crece a razón de 0,3 μm/m por cada grado Kelvin que la temperatura se desvía de 20 °C. A una temperatura de 30 °C, la incertidumbre del polinomio es de 3 μm/m.
Lo único que se necesita para calcular la corrección es conocer el coeficiente de dilatación térmica del material y la temperatura ambiente.
 Autocalentamiento
Autocalentamiento
Es el aumento de temperatura resultante de la transformación de energía eléctrica en la galga extensométrica. La generación de calor se determina mediante la expresión:

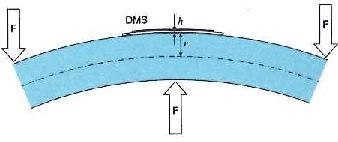
Para un valor efectivo de tensión de alimentación del puente de 5 V y una resistencia de la galga extensométrica de 120 Ω, el calor resultante es de 52 mW. Una galga extensométrica con una rejilla de medición de 0,6 mm, aplicada con una capa fina de adhesivo sobre un sustrato de acero o aluminio, puede ceder una parte importante de ese calor al objeto de medición. A pesar de ello, se genera una pequeña diferencia de temperatura entre la galga extensométrica y el objeto de medición, que produce una deformación aparente (ver arriba):

Si la temperatura de la galga extensométrica ajustada es superior a la del material en tan solo un grado Kelvin, se produce una deformación aparente de -11 μm/m (acero ferrítico) o de -23 μm/m (aluminio). La incertidumbre de medida se puede determinar de forma aproximada con un experimento sencillo: conectando la tensión de alimentación sin aplicar carga al componente. Durante la fase de aumento de la temperatura, se produce una ligera deriva de la lectura (deriva del cero). La máxima diferencia entre las lecturas que se registra durante este proceso de compensación térmica equivale aproximadamente a la máxima desviación esperada.
Una solución a este problema es el empleo de tensiones de alimentación más bajas (1 V genera solo 2 mW). En este sentido, también es ventajoso emplear galgas extensométricas con resistencias más altas.
En el caso de componentes con mala conducción del calor (plásticos, etc.) y cuando se utilizan galgas extensométricas muy pequeñas, es indispensable reducir la tensión de alimentación. Siempre se debe tener cuidado cuando se trabaja con cambios rápidos de temperatura. Los efectos de compensación derivados del ajuste de la lámina metálica de la galga extensométrica al material objeto de la prueba son constantes a lo largo del tiempo.