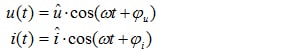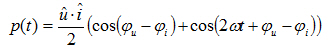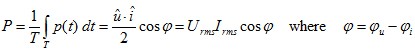Introduction
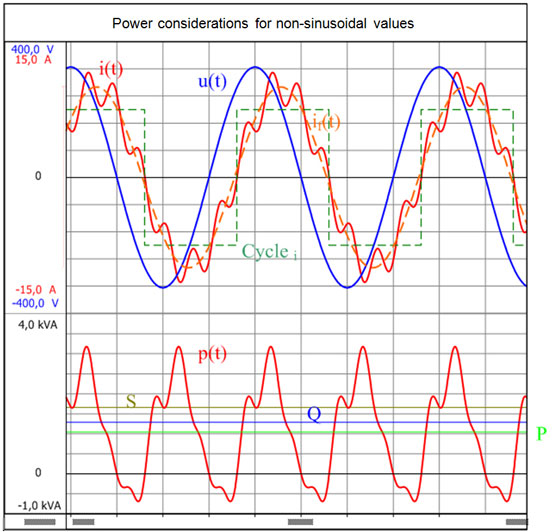
Les machines électriques convertissent l’énergie électrique en énergie mécanique. La direction du flux d’énergie est identifiée par la désignation du mode de fonctionnement de la machine électrique. En mode Moteur, l’énergie électrique est convertie en énergie mécanique. En mode Générateur, la machine électrique est entraînée et convertit l’énergie mécanique en énergie électrique. Les convertisseurs d’énergie sont caractérisés par l’énergie convertie par unité de temps plutôt que par l’énergie convertie. Cette valeur est appelée Puissance instantanée ou p(t)/ ![]()
| (1.01) |
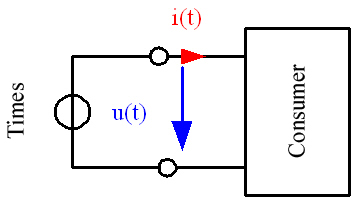
Fig 1.1 illustre un circuit 2 fils avec source d’énergie et module consommateur d’énergie associé. La tension appliquée u(t) et le courant consommé i(t) peuvent être mesurés. La puissance instantanée est dérivée du produit de ces deux variables :
![]()
| (1.02) |
Le sens des flèches présenté en Fig 1.1 montre comment le module consommateur d’énergie absorbe la puissance lorsque la puissance instantanée est positive (p(t) >0). Si la puissance instantanée est négative (p(t) <0), le module consommateur réinjecte de la puissance dans la source d’énergie.
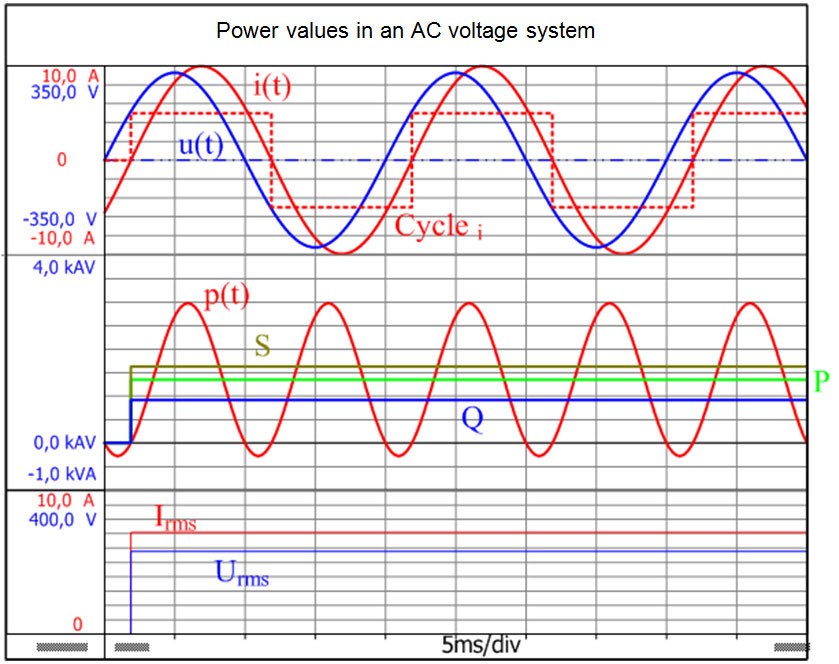
La valeur moyenne de la puissance instantanée p(t), sur la durée d’un cycle T, est connue en ingénierie électrique comme la puissance effective P.
![]()
| (1.03) |
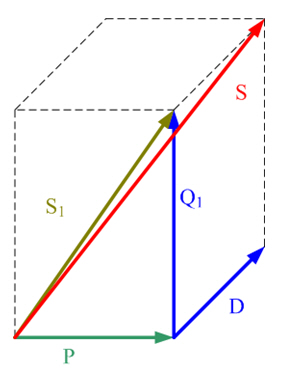
Le processus pour déterminer les puissances active, réactive et apparente dans Perception, à partir des courbes de tension et de courant, est détaillé ci-dessous.
L’implémentation de la formule (1.03), dans le logiciel Perception, est présentée à partir de l’exemple de la formule extraite de la librairie de fonctions Perception (1.04).

| (1.04) |