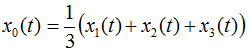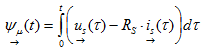Calcul du champ de vecteurs et du couple magnétique d'entrefers sur les moteurs asynchrones à l’aide de Genesis HighSpeed et Perception

Dû à leur conception simple et robuste, les moteurs asynchrones sont souvent utilisés dans les transmissions électriques. La Fig. 2.1 présente un moteur asynchrone de type cage d’écureuil. Le stator fixe présente trois bobinages. Le type cage d'écureuil est conçu à partir de barreaux d’aluminium ou cuivre et court-circuité avec des anneaux conducteurs aux extrémités du rotor.

L’application des courants, déphasés 3 fois sur les bobinages décalés dans l’espace, produit un champ magnétique rotatif. Ce champ magnétique tourne à la vitesse synchrone de rotation de:  

(2.01)

L’équation 2.01 illustre que la vitesse de rotation synchrone dépend de la fréquence  f_S

des courants sur le stator et du nombre de paires de pole p sur le moteur asynchrone.

Le champ magnétique passe au travers du rotor à cage d’écureuil. Ce déplacement induit des tensions dans les barres conductrices. En raison des anneaux de court-circuit en extrémité du rotor, des courants forts, résultant des tensions induites, traversent les barres conductrices. Suivant la loi de Lenz, des forces sont générées qui accélèrent le rotor suivant la direction du champ magnétique de rotation. Cela participe à réduire la différence de vitesse de rotation entre le rotor et le champ rotatif.

Fig. 2.1: Structure d’un moteur asynchrone avec rotor en cage d’écureuil
a) plan en coupe et b) plan de section longitudinale du moteur

2.1 Champ de vecteurs

En 1959, Kovacs a développé la théorie des champs de vecteurs pour faciliter la description mathématique des systèmes triphasés. Elle est souvent mise en pratique pour décrire les méthodes de contrôle des moteurs asynchrones. Les paramètres électriques et magnétiques d’un système triphasé peuvent être cartographiés sur un système orthogonal à 2-phases et sur un système séquence-zéro valable dans certaines circonstances. Le système orthogonal à 2-phases peut être interprété comme un nombre complexe appelé vecteur de champ. Ses parties réelle et imaginaire correspondent aux projections de ce nombre complexe, appelé vecteur de champ et représenté graphiquement comme tel, sur les axes, α et β dans le plan complexe.

L’équation 2.02 définit les règles de calcul pour le vecteur de champ à partir des valeurs des 3 phases x₁, x₂ et x₃ :

(2.02)

Prenant α comme opérateur complexe. Le système séquence-zéro associé est calculé comme suit :

(2.03)

La Figure 2.2 présente le champ de vecteurs dans le système de coordonnées orthogonal. La partie réelle est trace sur l’axe des abscisses α et la partie imaginaire sur l’axe des ordonnées  β. Les valeurs de phase sont obtenues par projection du vecteur de champ sur les axes a, b, c décalés de 120°.

Fig. 2.2: Champ de vecteurs dans le plan complexe

2.2 Schéma de circuit équivalent d’un moteur asynchrone au travers des champs de vecteurs

Le fonctionnement des moteurs électriques est souvent décrit au travers de schémas de circuits équivalents. La Fig. 2.3 présente le schéma de circuit équivalent simplifiéd’un moteur asynchrone au travers d’un champ de vecteurs. La tension stator appliquée au moteur asynchrone, via le convertisseur, est représentée par un vecteur de champ. Le courant stator passe dans le moteur asynchrone. Dans le schéma de circuit équivalent, la résistance de stator est représentée R_s. L’inductance L_μ représente l’inductance magnétique du moteur. Les inductances de fuite du moteur sont combinées dans L_σ. R_y désigne la résistance du rotor vu du côté stator. La vitesse de rotation mécanique n, de l’arbre du moteur asynchrone, est prise en compte dans le schéma de circuit équivalent au travers de la fréquence angulaire électromécanique ω. Ces 2 valeurs peuvent être converties l’une et l’autre à partir du nombre de paires de pôles ρ.
(2.04)

Pour de plus amples information sur le moteur asynchrone, veuillez-vous référer, par exemple, à  [2].

Fig. 2.3: Schéma de circuit équivalent simplifié d’un moteur asynchrone

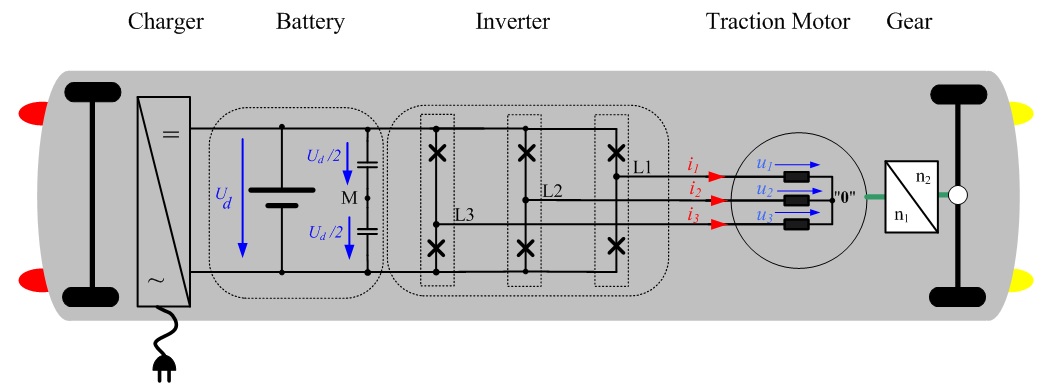
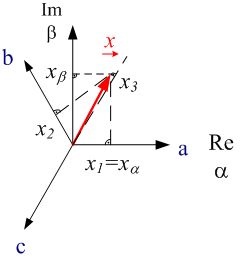
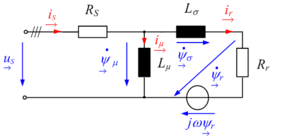
La Fig. 3.1 présente les courbes temporelles tensions de phase(u₁(t),u₂(t),u₃(t) et courants de phase (i₁(t),i₂(t),i₃(t)) d’un moteur asynchrone alimenté par convertisseur de fréquence. Le sens de mesure des tensions et courants est présenté dans la figure 1.1. Les valeurs des vecteurs de champ peuvent être calculées, à partir des valeurs de phase mesurées ; en utilisant l’équation 2.02. En raison du fait que Perception ne gère que des nombres réels, les parties réelle et imaginaire des vecteurs sont calculées séparément. L’équation suivante présente le calcul pour une tension et un courant de phase.

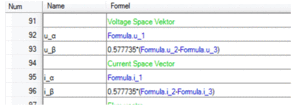
(3.01)

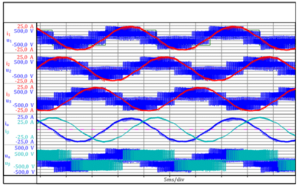
Fig. 3.1: les valeurs (i₁,i₂,i₃,u₁,u₂,u₃) et leurs vecteurs de champ calculés (i_a,i_b,u_a,u_b) (Pour les utilisateurs Perception, ces mesures sont disponibles dans les fichiers suivants :  Space Vector and Air GapTorque .pNRF. Ce fichier est disponible en téléchargement depuis notre site HBM).

3.1 Calcul du flux stator dans un moteur asynchrone

Le vecteur de champ Flux stator  décrit le champ magnétique dans un moteur asynchrone. Ce vecteur flux stator est obtenu par intégration de la différence entre la tension stator et la chute de tension à la résistance stator R_s du moteur.

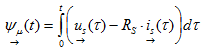
(3.06)

La faible valeur de résistance stator peut souvent être négligée, sur certains moteurs, suivant la précision attendue. En résultat de cette intégration, le flux stator est une valeur continue.  Toutefois, comme représenté Fig. 3.1, la tension stator présente une forme d’onde PWM (Pulse Width Modulated), les parties réelle  ψ_α(t) et imaginaire ψ_β(t) du vecteur de champ stator sont presque sinusoïdales (Fig. 3.2a). En approximation, la trajectoire du vecteur de champ flux stator est circulaire. Le rayon de cette trajectoire circulaire correspondant à l’amplitude du flux stator.

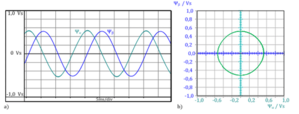
Fig. 3.2: Vecteur de champ flux stator  d’un moteur asynchrone

a) courbes temporelles des parties réelle et imaginaire
b) trajectoire du vecteur dans le plan complexe

3.2 Calcul du couple magnétique entrefers sur un moteur asynchrone alimenté par convertisseur  

Sur un moteur asynchrone, le couple magnétique interne entrefers peut être calculé à partir des mesures de tension, courant ou flux. Le couple magnétique interne entre fers représente la combinaison des couples de friction internes et du couple de l’arbre moteur. Si l’on minimise les couples de friction, le couple interne calculé correspond au couple mécanique de l’arbre qui peut être mesuré très précisément à l’aide d’un capteur de couple [3].

La précision du couple calculé dépend du modèle de calcul et de la précision des paramètres moteur utilisés. Le calcul du couple interne peut être utilisé comme information de vérification redondante de la mesure faite avec un capteur de couple, car les 2 valeurs devront présenter les mêmes ordres de grandeur en amplitude. De plus, le couple proportionnel d’un moteur électrique pourra être corrélé au couple total mesuré en sortie de la transmission, via un capteur de couple mécanique. Une application possible, sur un véhicule hybride par exemple, pourra être la caractérisation et différentiation des couples apportés par le moteur électrique et par le moteur à combustion sur le couple total en sortie d’arbre.

Comme illustré dans la littérature [2] le couple interne d’un moteur asynchrone peut être calculé à partir des courants stator et flux magnétiques stator .

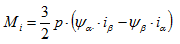
(3.06)

Dans ce cas, ρ représente le nombre de paires de pôles du moteur asynchrone. Courants et flux sont représentés par leurs vecteurs de champ. La Fig. 3.3 illustre les courbes temporelles des courants et flux stator ainsi que le couple magnétique interne entrefersM_i calculé p partir de ces valeurs. La sur-oscillation du couple est clairement visible. Cette sur-oscillation haute-fréquence du couple est générée par les commutations haute fréquence du convertisseur. Il est essentiel d’identifier la période du fondamental du courant sur le moteur pour que Perception puisse calculer le couple magnétique entre fers.

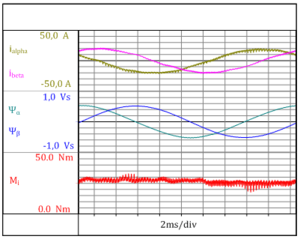
Fig. 3.3: Réponse temporelle du courant stator (i_α, i_β), flux stator (ψ_α, ψ_β) et du couple magnétique entrefers M_i

Cette publication présente les mesures faites sur un moteur asynchrone alimenté par un convertisseur. Les mesures par phase sont converties en valeurs de vecteurs de champ pour faciliter l’interprétation des mesures. Le flux magnétique dans un moteur asynchrone est calculé au travers de l’intégration de la tension stator. Les valeurs électriques mesurées combinées avec les valeurs magnétiques calculées permettent le calcul du couple magnétique interne entre fers du moteur asynchrone. Ce calcul du couple fournit une information redondante et complémentaire de celle mesurée à partir d’un capteur de couple mécanique haute précision. Les valeurs de couple calculées permettent de vérifier la véracité des mesures de couple mécanique et d’identifier rapidement les erreurs de mesures.

Références

[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft; Tagungsband 3. Tagung Innovation Messtechnik; 14. Mai 2013

[2] J. Teigelkötter: Energieeffiziente elektrische Antriebe, 1. Auflage, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3

[3] R. Schicker; G. Wegener: Drehmoment richtig messen; Hottinger Baldwin Messtechnik GmbH 2002, ISBN 3-00-008945-4  

[4] Berechnung von Leistungsgrößen mit Perception-Software
https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/

[5] www.hbm.com

Space Vector and Air GapTorque.pNRF