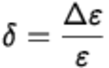Articles : Exactitude des mesures en analyse expérimentale des contraintes - Partie 1

Depuis des dizaines d’année et à plusieurs reprises, la technologie des jauges de contrainte a été largement optimisée notamment sur la compensation des erreurs. Mais il y a tout de même certaines influences qui peuvent affecter les mesures. L’objectif des articles est d’une part de préciser ces nombreuses sources d'erreur potentielles (souvent évitables) quand on travaille avec des jauges et d’autre part de vous aider à déterminer l'incertitude de mesure que vous pouvez avoir et cela dès la conception de votre projet.

Mesures relatives au point zéro

Par mesures relatives au point zéro, il faut entendre des mesures concernant des valeurs mesurées courantes avec les valeurs mesurées obtenues au début de la mesure sur plusieurs semaines, mois ou même années. Aucune « remise à zéro » de la chaîne de mesure n'est exécutée entre temps. Les mesures relatives au zéro sont bien plus critiques que des mesures non relatives non au zéro, parce que les dérives de zéro (résultant d’une variation de la température ou d'autres influences) sont entièrement intégrées au résultat de mesure.

Les erreurs de zéro sont particulièrement dangereuses pour de petites valeurs de contrainte, parce que proportionnellement ces dérives relatives deviennent conséquentes par rapport à la valeur mesurée. Les contraintes générées sur des composants et structures de machine sont souvent d’à peine 100 µm/m, parce généralement un facteur de sécurité important est appliqué sur le dimensionnement des machines au moment de la construction. Dans ce cas une dérive de zéro de 100 µm/m, a pour conséquence une erreur de mesure de 100 %.

Étant donné qu'une mesure continue de surveillance structurale est presque toujours une mesure relative au point zéro, une attention toute particulière doit être portée sur la protection des jauges de contrainte contre les éventuelles influences environnementales. Il est essentiel que le point de mesure soit d’une stabilité suffisante sur le long terme. Comme de grandes variations de température doivent être prévues, les coefficients de température doivent être petits. De faibles amplitudes de signal de mesure sur des composants généreusement dimensionnés sont susceptibles d'être superposées par des effets résultant d’une déficience d'installation d’une jauge de contrainte. L'électronique de mesure répond alors à chaque variation de résistance par un changement à l’affichage.

Ceci peut être dû à un changement de la grandeur mesurée ou, aussi, à l'admission de molécules d'eau. La valeur réelle mesurée, comme signal composé de toutes les proportions de contrainte à la jauge, ne permet pas de faire une distinction entre les proportions de contraintes voulues et non désirées.

Mesures non relatives au point zéro

Les mesures non relatives au point zéro signifient des mesures prises pendant des campagnes de mesure qui permettent à des moments spécifiques un équilibrage à zéro sans aucune perte d'information. Seule la variation de la grandeur mesurée intervenant après « l’équilibrage à zéro » est prise en compte. (Des balances modernes de salle de bains sont automatiquement tarées chaque fois qu'elles sont mises sous tension, sans perte d'information.) « L'équilibrage à zéro » est souvent possible lors d’essais de charge uniques (souvent sous forme de mesures à court terme), par conséquent les dérives zéro sont totalement insignifiantes.

Dans des essais destructifs se produisent des contraintes très élevées, cela signifie qu’il faut des jauges de contrainte avec des gammes de mesure adéquates. Il est vraiment embarrassant et parfois coûteux de devoir changer des jauges mal adaptées après des semaines de travaux préparatoires.

Dans les laboratoires et halls d’essais, les mesures sont considérées moins critiques, car les conditions ambiantes (température, humidité) sont assez modérées.

Les mesures effectuées dans des chambres à atmosphère contrôlée ou bien sur le terrain sont plutôt critiques.

Fig. 1 : Schéma des différentes influences sur le signal d'un point de mesure équipé de jauges de contrainte

Composants de la chaîne de mesure

Dans un souci de clarté et de compréhensibilité, seul l’état d’une contrainte uni-axiale sera étudié ci-dessous. Le schéma (fig. 1) montre le cheminement du signal de mesure. Il montre également les éléments influents et leurs effets sur les différents composants de la chaîne de mesure. Ces caractéristiques et effets sont indiqués en bleu s'ils peuvent affecter le point.

Objet de mesure (DUT)

Quand l'objet de mesure à tester est chargé, une contrainte σ est générée dans le matériau. Cela occasionne une déformation du matériau qui se comporte inversement proportionnellement au module d'élasticité. Cette déformation du matériau peut être déterminée en mesurant la déformation en surface au moyen d'une jauge de contrainte.

Le module d'élasticité présente une certaine incertitude (tolérance du module d'élasticité). Les essais sur des aciers de construction ont montré un taux de variation de 4.5% et la température agit également sur ce module d'élasticité qui devient un élément d'influence sur l’incertitude.

Si la jauge de contrainte est collée sur une surface convexe, par exemple une tige, la contrainte sur la grille de mesure est plus élevée que sur une surface plane.

La raison de ce constat est la distance par rapport à la fibre neutre : plus la grille de mesure est proche de cette autre fibre neutre et le composant fin, plus la valeur mesurée devient forte. L'épaisseur de l'adhésif et de la jauge de contrainte jouent une faible rôle. Le changement de température ∆t agissant comme le coefficient de température de dilatation du matériau participent également à la dilatation thermique, ce qui est significatif pour des mesures faites par rapport au zéro absolu.

Les effets de répercussions élastiques (provoquées par des processus de relaxation dans la microstructure du matériau) causant une contrainte du matériau tendent à diminuer légèrement après le chargement spontané. La formule donnée au-dessus montre donc plusieurs incertitudes.

Index des formules

Installation

La grandeur d’entrée requise est la contrainte du matériau. Dans un cas idéal, elle est identique à la contrainte réelle de la grille de mesure de la jauge de contrainte :

En réalité et dans la pratique, l'alignement de la jauge et d'autres erreurs d'installation se produisent en dépit du grand soin que l’on peut apporter lors de l’installation. La jauge se comporte comme un élément de ressort. Soumises à des charges, la grille de mesure subie une déformation et les points de rebroussement de cette grille influencent le comportement mécanique. Les propriétés rhéologiques de l'adhésif et du support de jauge agissent également. Il y existe aussi ce qu’on appelle une hystérésis légère. (Dans la construction de capteur, le dimensionnement des points de rebroussement est déterminé avec précision de manière considérablement le fluage, qui produit une contrainte additionnelle indésirable, en ajustant les longueurs des points de rebroussement de la grille de mesure). Dans les applications ESA, cette compensation pourrait être mise en œuvre mais elle nécessite beaucoup d'efforts, génère de nombreuses dépenses et comme elle n'est généralement pas nécessaire, elle n’est pas employée. Une contrainte plus importante peut aussi se produire lorsque nous avons à faire à une surface incurvée (voir ci-dessus).

Si les points de mesure ne sont pas suffisamment protégés contre l'humidité, l'adhésif et le support de jauge peuvent absorber cette humidité et se gondoler. Cela se traduira immédiatement en source d'erreur sous la forme d’une contrainte spécifique aléatoire sur la jauges de contrainte.

La teneur en humidité affecte également la stabilité des valeurs mesurées comme dans toutes les méthodes de mesure (voir ci-dessous la résistance d’isolation d’une jauge). Particulièrement dans les mesures faites par rapport au point zéro, l’ingénieur mesure ne peut être certain d’observer la contrainte exercée dans le matériau ou s’il s’agit aussi de contraintes dues aux autres effets décrits ci-dessus. Pour cette raison, la protection du point de mesure est extrêmement importante. C’est une condition essentielle à respecter pour obtenir des résultats fiables, particulièrement dans ces mesures relatives au zéro absolu.

Tous les phénomènes décrits ici produisent un effet de contrainte sur la grille de mesure qui ne correspond pas exactement à la contrainte réelle exercée dans le matériau.

Jauges de Contrainte

La jauge de contrainte convertit la contrainte exercée dans la grille de mesure en variation de résistance proportionnelle à la contrainte.

La tolérance du facteur de K et sa sensibilité de température contribuent à l'incertitude.

Il convient de noter que si la jauge doit être installée sur un matériau no homogène, la moyenne de la contrainte sous la grille de mesure est mal convertie en variation de résistance. En effet, si la longueur active de la jauge est mal choisie, les valeurs de contrainte mesurées seront trop petites ou trop grandes. C'est particulièrement important quand l’on veut déterminer des valeurs maximales d’effort mécanique.

La réponse en température de la jauge de contrainte affecte le point zéro. Elle a un grand impact quand nous avons de grandes différences de température mais aussi lorsqu’on utilise des jauges de contrainte qui sont mal adaptées au coefficient de dilatation thermique du matériau (DUT), puisqu'elles n’ont pas les capacités de réaliser une compensation.

L’effet d’auto-échauffement (effet du courant électrique circulant dans la jauge de contrainte) a un résultat similaire tout aussi néfaste, car il mène à une différence de température entre le matériau et la jauge de contrainte. C'est la raison pour laquelle, il est préconisé d’utiliser des tensions d’excitation très basses ce que les amplificateurs de mesure modernes proposent. Certes, la tension de sortie du pont de jauges sera faible mais ces électroniques peuvent les amplifier sans difficulté. Cependant, la prudence est conseillée avec des matériaux minces et les matériaux qui absorbent peu la chaleur.

Dans le cas de contraintes alternatives fréquentes de grande amplitude (> 1500 µm/m), il peut se produire une fatigue du matériau constituant la grille de mesure avec pour résultat une dérive du zéro.

Il existe aussi une sensibilité transversale de la jauge de contrainte. Mais elle ne produit aucune dérive significative. Dans un état de contrainte uni-axial, la sensibilité transversale est prise en compte par la détermination expérimentale du facteur K.

Une variation de linéarité jusqu'à 1000 µm/m est négligeable en analyse de contrainte.

La pénétration de l'humidité dans une jauge réduit la résistance d'isolation, ce qui cause un shunt de résistance aux points de raccordement de la jauge de contrainte et cela se traduit généralement par une instabilité dans l'affichage des valeurs mesurées. Les jauges de contrainte de faible impédance sont moins sensibles à l'influence de l'humidité.

Amplificateur de mesure

Le signal d’entrée de l'amplificateur de mesure correspond à la variation de résistance de la jauge de contrainte.

Cette variation de résistance est très petite (à 1000 µm/m et avec un facteur K de 2 c'est de l’ordre de 0.2 % soit 0.24 Ω sur une jauge de 120 Ω). En analyse expérimentale des contraintes on raccorde souvent une seule jauge sur l’amplificateur. On parle dans ce cas d’un quart de pont. On ferme alors en pont de Wheatstone à l'aide de trois résistances fixes (habituellement situées dans l'amplificateur de mesure). Un montage en demi - pont (deux jauges) et pont complet (quatre jauges) permet de réduire ou d’éliminer des erreurs qui ne seront pas traités ici dans cette page.

Seul le raccordement d’une seule jauge (montage en quart de pont) est présenté ici. Habituellement la corrélation entre le déséquilibre de pont et le changement résistance est décrite avec la formule

La corrélation actuelle montre un faible degré de non-linéarité, qui sera examiné plus en détail ci-dessous.

L'amplificateur de mesure fournie la tension d'alimentation du pont de jauge, amplifie le signal de mesure provenant des jauges et délivre le signal de mesure à l’opérateur.

Nous pouvons volontairement exclure les erreurs qui peuvent se produire en raison de la résistance des câbles longs, des parasites extérieurs, des tensions thermoélectriques et de l'électronique de mesure elles-mêmes. Celles-ci peuvent être presque entièrement évitées en employant les technologies bien connues proposées par HBM (câblages 3, 5 ou 6 fils, circuit Kreuzer étendu, blindages, amplificateurs de mesure modernes à fréquence porteuse).

Tolérance du module d'élasticité

Le module d'élasticité (spécifié par le fabricant) dispose d’une incertitude (tolérance du module d'élasticité) qui peut être de plusieurs pour cent. Déterminer exactement le module d'élasticité d’un matériau au sein d’un laboratoire approprié est une opération coûteuse et bien souvent ne peut pas être mise en oeuvre.

Dans les mesures expérimentales des contraintes que nous appelons ESA, l'incertitude relative du module d'élasticité génère une incertitude relative identique dans la mesure de contrainte.

data-htmlarea-file-uid=

Cela signifie que si le matériel a un module d'élasticité avec une valeur d’incertitude connue de 5%, elle seule crée une incertitude de mesure de 5% sur la contrainte.

Le module d'élasticité dépend également de la température grandeur d'influence importante. Le coefficient de température du module d'élasticité (pour un acier = -2 • 10^-4/K). Le changement relatif du module d'élasticité se fait donc selon la formule suivante :

data-htmlarea-file-uid=

C’est équivalent à l’incertitude additionnelle de la contrainte mécanique.

data-htmlarea-file-uid=

Par exemple : Si le module d'élasticité d'un acier est donné pour une température de 23°C et que la mesure s’effectue à 33°C, le module d'élasticité chute de 0.2%. Si cet effet n'est pas compensé par calculs, il y aura donc une dérive de 0.2% en plus de la tolérance spécifique du module d'élasticité. Noter que la dérive TC du module d'élasticité est elle-même dépendante de la température, alors cela signifie que cet influence ne peut jamais être entièrement compensée.

Index des formules

Estimation de l'incertitude de mesure pour des mesures réalisées sans tenir compte du point zéro

Un élément important de ce type de mesure est que le point zéro est inutile pour analyser les résultats de mesure. En effet, seuls les changements de la grandeur mesurée sont pris en compte et le point zéro ne varie pas pendant la mesure (typiquement des essais relativement courts). Nous pouvons citer les essais de chocs, les essais de traction et les essais de chargement brefs.

Les répercussions du matériau et le fluage des jauges de contrainte peuvent être quelque peu importants dans des mesures sans tenir compte du point zéro et sont donc abordés dans cette page. D'autre part, les phénomènes tels que la dilatation thermique, le grossissement de l'adhésif, la chute de résistance d'isolation, la réponse en température la résistance en fatigue des jauges de contrainte sont peu pertinents dans ce type de mesure.

Naturellement, la résistance ne peut pas tellement chuter lorsqu’il s’agit d’essais courts et ne peut entrainer un problème sur le point mesure.

Rayon de courbure des objets soumis à une charge de flexion (augmente la contrainte)

Fig. 2 : Jauge de contrainte placée sur une pièce soumise à une charge de flexion

Si la jauge de contrainte est placée sur un composant qui fléchit longitudinalement à la grille de mesure, la contrainte de la grille de mesure dévie par rapport à la contrainte mécanique appliquée (fig. 2). Les valeurs mesurées obtenues sont trop grandes. Plus le rayon de courbure est petit et plus la distance de la grille de mesure de la surface de l’objet est grande, plus l'effet est grand.

Si la jauge de contrainte est située dans la partie concave, les valeurs mesurées seraient également trop grandes. Le facteur décrivant l'erreur de mesure serait identique. Cela a également comme conséquence une multiplication de la dérive par rapport à la valeur mesurée. L'équation des calculs est :

data-htmlarea-file-uid=

Pour une distance moyenne de 100μm de la grille de mesure par rapport à la surface de l’objet et un rayon de courbure de 100 millimètres, l'augmentation résultant de la contrainte est de 1/1000 par rapport à la valeur de contrainte. La contrainte réelle de l’objet dans cet exemple est 0.1% inférieure à la contrainte mesurée. Cela signifie que la contrainte mesuré de 0.1% trop grande. Cette erreur de mesure est clairement appliquée seulement pour de petits rayons de courbure.

Répercussions élastiques

Pour beaucoup de matériaux, la contrainte augmente toujours légèrement après un chargement mécanique spontané. Ce phénomène est en grande partie atténué après environ 30 minutes (acier à 23°C) et se produit également quand la charge est enlevée. Le quotient de la quantité de cette contrainte additionnelle et de la contrainte spontanée dépend largement du matériau. Les répercussions matérielles produisent ainsi une erreur de mesure (positive) additionnelle. Ceci se produit seulement en acquérant les valeurs de contrainte. Cette dérive peut donc être presque totalement évitée dans de nombreux cas de mesure.

Cependant, si la valeur mesurée est acquise longtemps après que la charge soit appliquée et que la contrainte du matériau a augmenté de 1% (par rapport à la contrainte spontanée), le résultat sera que la valeur mesurée pour la contrainte matérielle est 1% trop grande.

Désalignement de la jauge de contrainte

Si la jauge de contrainte n'est pas exactement alignée dans la direction de la contrainte (cas d’une contrainte uni-axiale), nous avons une erreur de mesure négative. La contrainte mesurée sera alors inférieure à la contrainte réelle. L'erreur relative de contrainte est déterminée ainsi :

data-htmlarea-file-uid=

Une erreur d'alignement de 5 degrés et un coefficient de Poisson de 0.3 (acier) a pour conséquence une erreur de contrainte de -1%. Ainsi, la contrainte réelle et la contrainte matérielle sont 1% plus grandes.

Fluage de la jauge de contrainte

Une fois que la contrainte matérielle soit induite spontanément, la grille de mesure de la jauge se relâche légèrement. Le processus, déterminé principalement par les propriétés mécaniques de l'adhésif et de la géométrie de la jauge (les grilles de mesure courtes sont assez critiques, les jauges avec des longueurs très longues ne font pas sujet au fluage), dépend également de la température. Après fluage la contrainte de la grille est légèrement moindre que la contrainte matérielle. La jauge de contrainte très souvent employée en ESA (modèle LY11-6/120 de HBM avec une longueur de grille active de 6 mm) avec la colle Z70 (HBM) à une température de 23°C présente un retour de fluage d’environ 0.1% en une heure. C'est équivalent à une erreur de mesure négative de -0.1% par rapport à la contrainte mesurée. Naturellement la dérive sera moindre si la valeur mesurée est déterminée juste après le chargement spontané. En raison du signe négatif, le fluage d’une jauge de contrainte compense au moins partiellement les répercussions élastiques et peut donc souvent être complètement ignoré en ESA. Cependant, nous conseillons la prudence en employant d'autres adhésifs à températures élevées. Par exemple, la colle X60 (HBM) appliquée à70°C avec une contrainte de 2000 μm/m, la dérive résultante après juste une heure est de -5%.

Hystérésis de la jauge de contrainte

La même chose s'applique pour l'hystérésis : les grilles de mesure courtes semblent être plus critiques et l'adhésif a un certain effet. L'hystérésis pour une jauge de contrainte LY11-6/120 est seulement de 0.1% à une contrainte de ±1000 μm/m si la colle Z70 est employée comme adhésif. Elle est donc négligeable.

Si une jauge de contrainte très petite (LY11-0.6/120) avec une longueur de grille active de 0.6 mm doit être employée alors l'hystérésis augmentera et avec elle l'incertitude de mesure jusqu'à 1%.

Facteur de jauge

Tolérance sur le facteur de jauge

Il faut ajuster exactement la chaine de mesure sur la valeur nominale du facteur de jauge (spécifié par le fabricant sur le paquet des jauges). Ce facteur décrit la corrélation entre le changement de contrainte et le changement de résistance. Il a été déterminé expérimentalement par le fabricant. L'incertitude du facteur de jauge est généralement de 1%. Le facteur de jauge produit le même niveau d'incertitude de mesure des contraintes et des déformations.

Coefficient de température du facteur de jauge

Le facteur de jauge dépend la température. Le signe et la valeur de cette dépendance sont déterminés par l'alliage de la grille de mesure. Le fait que le TC du facteur de jauge lui-même tributaire de la température peut être ignoré en ESA. Le TC d’une grille de mesure en Constantan est d’environ 0.01% par degré Kelvin. Ainsi, le facteur de jauge diminue de 0.1% pour une augmentation de température de 10 K, ce qui est généralement négligeable. Si les mesures étaient effectuées à 33°C, les valeurs de contrainte augmenteraient juste de 0.1%.

Mais à 120°C, il serait de 1%, c’est à considérer.

Longueur de la grille de mesure

Il faut bien comprendre que la jauge intègre les contraintes sous la surface active de sa grille de mesure. Si l’état de contrainte sous cette surface est non homogène, le changement de résistance ne correspondra pas à la plus grande contrainte locale, mais plutôt à la contrainte moyenne sous la grille active. Cela est préjudiciable, parce que c'est particulièrement les plus grandes contrainte qui ont un intérêt. Les valeurs mesurées sont donc en deçà des valeurs maximum désirées, menant à des dérives négatives.

Puisque ce phénomène est bien connu, de même que les contre-mesures (grille de mesure courte), des erreurs importantes se produisent rarement dans les applications pratiques. Néanmoins, prenons un exemple : La mesure s’applique à une contrainte de flexion au bout d’une lame. La jauge de contrainte acquiert sous sa grille de mesure la contrainte moyenne (fig. 3). Les contraintes se comportent comme des efforts :

data-htmlarea-file-uid=

La valeur maximum de contrainte qui est réellement recherchée pourrait facilement être déterminée dans ce cas simple avec un calcul de correction. Si celui-ci n'est pas fait, un écart du résultat de mesure se fera.

L’écart est :

data-htmlarea-file-uid=

Si dans l'exemple ci-dessus, une grille de mesure avec une longueur active de moins 2% de l2 est utilisée, l’écart sera moindre de 1% de la valeur mesurée.

Finalement le rapport de la contrainte maximum et de la contrainte mesurée dépend toujours de la distribution de la contrainte sous la grille de mesure. Si ceci est connu par un calcul d’élément fini, la valeur maximum désirée peut être calculée à partir de la moyenne arithmétique de la contrainte.

Naturellement, les écarts se produiront si la jauge de contrainte est mal placée. Ceci peut également être en grande partie évité et il doit l’être.

Fig. 3: Jauge sur une lame de flexion pour mesurer les contraintes

Fig. 4 : Installation d'une jauge dans un environnement sévère.

Erreurs de linéarité

Erreur de linéarité d’une jauge

Les jauges de contrainte avec des grilles de mesure (Constantan, Karma, Nichrome V, Platine-Tungstène) présentent une excellente linéarité. Bien que pour de grandes déformations certaines dérives peuvent être démontrées avec la grille de Constantan. La courbe caractéristique statique réelle peut être décrite (de façon empirique) par l’équation quadratique :

data-htmlarea-file-uid=

Si les déformations étaient déterminées selon la formule

data-htmlarea-file-uid=

Il n'y aurait aucune dérive de la linéarité. Cependant, comme la composante quadratique est simplement négligée dans les applications pratiques, l'erreur résultante devrait dans ce cas être indiquée. L’erreur relative de la valeur de contrainte déterminée par rapport à la valeur vraie est aussi grande que la contrainte elle-même :

data-htmlarea-file-uid=

Pour des contraintes jusqu'à 1000 μm/m, la valeur d’erreur relative de la contrainte ne dépasse pas 0.1%. C'est équivalent à 1 μm/m, ce qui est négligeable.

L’erreur de linéarité commence à être appréciée pour de plus grandes contraintes :

10 000 μm/m donne 1%
100 000 μm/m donne 10%

Pour un montage en quart de pont, heureusement ceci peut être en grande partie compensé.

Erreur de linéarité d’un montage en pont quart

Dans le cas d’un pont de Wheatstone en quart de pont, de petits changements de résistance sont généralement constatés. Avec ce montage, une seule jauge de contrainte équipe le point de mesure, cette solution est couramment employée en ESA. Les autres résistances fermant le pont sont indépendantes de la contrainte. La relation est dans ce cas :

data-htmlarea-file-uid=

Bien que le rapport soit non linéaire, la linéarité est assumée en pratique (si celle-ci est connue ou non) et l'équation devient

data-htmlarea-file-uid=

L’écart résultant de cette simplification peut être calculé avec l'équation.

data-htmlarea-file-uid=

Une contrainte de 1000 μm/m (avec k = 2) donnera une variation de 0.2% de la résistance.

L'erreur de mesure relative déterminée avec l'équation 17 est de -0.1%. C'est équivalent à une variation absolue de -1 μm/m. La déviation de la valeur vraie est négligeable.

Les erreurs de linéarité commencent à se faire sentir pour de plus grandes contraintes comme précédemment indiquées ci-dessus :

10 000 μm/m > >> -1%,
100 000 μm/m >>> -9.1%.

Quand des jauges Constantan sont utilisées (non-linéarité semblable en termes de grandeur, mais signe opposé), les deux erreurs s’annulent en grande partie et donc n'ont pas besoin d'être considérées.

Il faut noter cependant qu'aucune compensation n'est jamais complètement réussie, particulièrement étant donné que le facteur de jauge varie légèrement de 2 et la courbe caractéristique statique réelle ne correspond pas exactement à l’équation empirique 12.

En résumé

Il est difficile de corréler les différentes incertitudes les unes aux autres. Cependant, elles peuvent être dans une certaine mesure avec des effets s’annulant (répercussions matérielles et fluage de la jauge, erreur de linéarité de la jauge et montage quart de pont). Par conséquent, il est permis de combiner les différentes incertitudes en faisant la somme quadratique des erreurs. Les valeurs en caractères gras ci-dessus sont employées pour obtenir un résultat pour l'exemple.

L'incertitude de mesure de contrainte est juste au-dessous des 3%. La mesure atteint presque 6% de la valeur mesurée.

Le pourcentage multiplié par la valeur mesurée donne la variation en μm/m ou N/mm2. L'incertitude du module d'élasticité est généralement responsable de la plus grande quantité d'erreur dans les mesures menées en ESA en ne tenant pas compte du zéro. Certaines incertitudes doivent être considérées pour des mesures faites par rapport au point zéro.

Estimation de l'incertitude de mesure pour des mesures relatives au point zéro

Dans ce type de mesure, le point zéro est important. En général, ces mesures se font sur de longues durées par exemple sur des bâtiments et dans le cas d’essais de fatigue sur des composants. Si le point zéro varie pendant les mesures, le résultat de mesure peut être entaché d’une erreur additionnelle. Les incertitudes de mesure déjà discutées dans la dernière partie de cette série doivent être ajoutées à celles notifiées dans cette partie.

Gonflement de la colle et de la grille de mesure

La cause principale de cet effet est la grande mobilité des molécules d'eau et des propriétés hygroscopiques des adhésifs et des matériaux du support. La conséquence est une dérive du zéro pas toujours clairement perceptible (ou distinguable des contraintes du matériau). Elle peut atteindre des valeurs considérables. On mesure ainsi une contrainte qui n'existe pas quand le composant est testé. Cette contrainte parasite est seulement partiellement réversible, ce qui est probablement due à l'hystérésis de sorption. Malheureusement il n'y a aucune façon « de saisir un sèche-cheveux » et de chasser les molécules d'eau. La vitesse à laquelle la valeur mesurée dérive dépend de la protection du poste de mesure et des conditions ambiantes. La constante de temps peut être dans la plage de plusieurs heures. Une température et une hygrométrie élevée sont particulièrement critiques. Malheureusement aucune formule ou figure concrètes ne peuvent être données ici.

Résistance d'isolation

Le résidu de flux du matériau peut également absorber des molécules d'eau. Ceci apparaît dans la pratique avec un e « exposition à la respiration » qui est souvent perceptible dans la fluctuation des valeurs mesurées. Les contrôleurs expérimentés identifieront l'avertissement et nettoieront méticuleusement tous les points de contact. « Soutenir » le résidu est également possible dans quelques circonstances. Cependant, tous ces contre-mesures exigent que les parties moites ne soient pas déjà incluses sous le produit de protection du point de mesure, qui est souvent là pour une bonne raison. Il est bien de pratiquer l’équipement du point de mesure sous une bâche, de la chauffer de quelques degrés par rapport à la température ambiante du moment et de le protéger immédiatement. Ceci exclura toute possibilité de condensation se formant plus tard sous la protection. Si les résistances d'isolation sont basses, il se produira une dérive de zéro. Les résistances d'isolation dans le montage en pont de jauges sont extrêmement critiques dans ce cas-ci. L'isolation électrique défectueuse des contacts de la jauge entre elles est comparable à un shunt de résistance. Elle ne peut pas être mesurée directement, mais en raison de sa nature, elle est semblable en grandeur à la résistance d'isolation. La corrélation entre la contrainte et le shunt apparents est donnée selon :

data-htmlarea-file-uid=

Cette équation montre que l'effet est inférieur avec les jauges de contrainte de haute résistance. Les erreurs de mesure suivantes sont déterminées pour des jauges de 120 Ω (facteur de jauge = 2) :

Dans des circonstances « normales », des résistances d'isolation plus grandes que 50 MΩ peuvent être réalisées et des dérives à moins de 1.2 μm/m sont négligeables.

Au 500 kΩ et avec une valeur mesurée de 1000 μm/m. l'erreur de zéro serait déjà de -12% ! Ceci prouve clairement qu'une baisse significative des résistances d'isolation pourrait faire échouer les mesures sur le point de mesure. Les capteurs à jauges de contrainte ont des résistances d'isolation de plusieurs GΩ.

Une hygrométrie élevée avec en même temps une haute température (comme de la vapeur saturée) est aussi critique parce qu'elle amène une haute pression de vapeur d'eaux. De minuscules molécules d'eau s’échappent et recouvrent graduellement la protection du point de mesure. Il est impossible de prévoir sans un essai si le poste de mesure se compromis après juste quelques jours ou plusieurs années.

Fatigue

Les signes de fatigue d’une grille de mesure de la jauge de contrainte apparaissent pendant les chargements dynamiques du composant et s’expriment par une dérive du zéro (contrainte apparente dans le matériau). Plus l'amplitude de contrainte alternative est grande et plus le nombre de cycles de charge est élevé, plus grand sera cet effet (fig. 5).

L'installation et la moyenne arithmétique de la contrainte affectent également la dérive du zéro. Si la moyenne est négative, la résistance à la fatigue s'améliore. Si la valeur est positive, elle se détériore. Pratiquement aucune dérive de zéro ne peut être prévue pour des contraintes alternatives avec une amplitude jusqu'à 1000 μm/m. De plus grandes amplitudes sont plus critiques. Une erreur de zéro de 10 μm/m peut être prévue pour :

1500 μm/m et environ 2 mil.de cycles de charge

2000 μm/m et environ 100 000 cycles de charge

2500 μm/m et environ 4000 cycles de charge

3000 μm/m et environ 100 cycles de charge

A noter que la pièce d'essai subit également de la fatigue. Si sa résistance aux charges alternatives est plus grande que celle de la jauge de contrainte, l'utilisation des jauges de contrainte optiques devrait être considérée (Réseaux de Bragg).

Fig. 5 : Dépendance de la dérive de zéro en fonction de l'amplitude de contrainte et du nombre de cycle de charge.

Résumé de toutes les incertitudes partielles

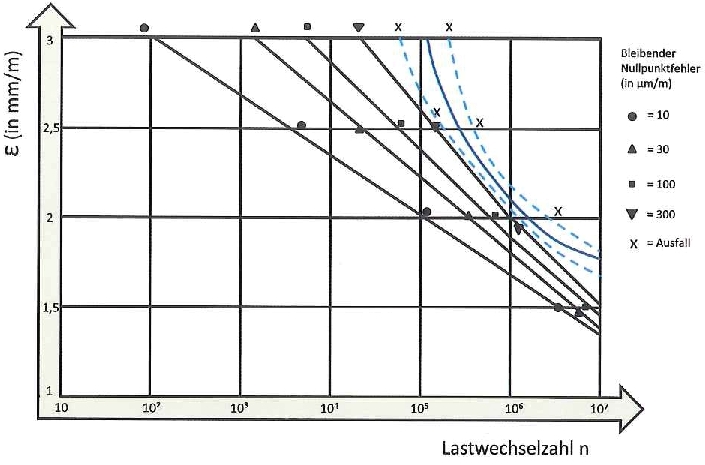
Alors que les dérives du paragraphe 3.3 sont multiplicatives en termes d’effet et sont indiquées en pourcentage de la valeur mesurée, les dérives dans cette section ont un effet additif. L'unité de mesure est le μm/m et elles sont pratiquement indépendantes de la valeur mesurée. Si la dérive relative est calculée avec l'équation

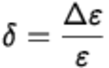
la valeur est comparable à celles du paragraphe 3.3

Si les valeurs en caractère gras ci-dessus sont combinées en utilisant l'addition de Pythagore, le résultat est de 16.01 μm/m. Comme les incertitudes de mesure ne devraient pas être arrondies, l'incertitude pour le point zéro est de 17 μm/m. Avec une contrainte de 1000 μm/m, la dérive exprimée en pourcentage est de 1.7%, ce qui est certainement raisonnable. Cela devient plus critique avec de faibles contraintes : 17 μm/m de 100 μm/m donnent déjà 17%.

Maintenant l'incertitude du point zéro (1.7% ou 17%) doit encore être ajoutée à l'incertitude du paragraphe 3.3 (3% pour la mesure de contrainte).

Le résultat selon l’addition de Pythagore est :

4% avec une valeur de mesure de 1000 μm/m,
18% avec une valeur de mesure de 100 μm/m.

Habituellement la contrainte mécanique est la grandeur mesurée réelle ainsi son incertitude doit être estimée. L'incertitude de la mesure de contrainte calculée dans la section 3.3 est de 6%. Y compris l'incertitude du zéro (1.7% ou 17%) avec l'addition de Pythagore, le résultat est :

7% avec une contrainte de 1000 μm/m,
19% avec une contrainte de 100 μm/m.

Les grandes erreurs relatives de mesure se produisent avec des mesures faites par rapport au point zéro, particulièrement quand il y a de faibles contraintes.

Jauges positionnées sur une structure métallique.

Jauges de contrainte installées sur la tête de rotor d'un hélicoptère.

Exemples d’équipements en extensométrie

Jauges de contrainte installées sur un rail.

Points de mesure avec jauges de contrainte sur un élément de structure de la plate-forme de recherche FINO 1, spécialement protégés pour un usage sous l’eau en Mer du Nord.

Rosettes placées sur un matériau composite (carte électronique).

Effet de l'installation

On a supposé jusqu'ici que l'installation du point de mesure avec des jauges de contrainte était bien étudiée et exécutée consciencieusement. Pour cette raison, seules quelques-unes des différentes dérives citées dans les exemples ci-dessus ont dépassé l’ensemble de la plage. Il est malheureusement nécessaire de préciser que si l'installation est très mal effectuée, les erreurs de mesure pourraient atteindre arbitrairement de grandes valeurs. Nous pouvons imaginer un instant qu'une jauge de contrainte de grande longueur soit employée pour essayer de mesurer une contrainte sur une entaille ou que les résistances de contact de la jauge de contrainte fluctuent de 0.24 Ω (équivalent à une erreur de contrainte de 1000 μm/m pour une jauge de contrainte de 120 Ω).

Particulièrement dans les mesures relatives au point zéro sur de longues périodes, l'importance de la protection du point de mesure ne peut pas être surestimée. Un excellent exemple est montré avec les 44 points de mesure avec jauges de contrainte sur la plate-forme de recherche FINO 1 (hauteur total 129 m) en Mer du Nord (à 45 kilomètres au nord de l'île de Borkum en Islande). Les jauges de contrainte sont placées de 5m à 25 m au-dessous de la surface de l'océan. Leur fonction était de mesurer les contraintes de chargement sur l'armature de soutien de la plate-forme provoquée par les piliers, les vagues et le vent. Après deux ans dans l'eau en Mer du Nord, 42 points sont toujours intacts et opérationnels.

Une autre grosse erreur peut se produire, la jauge est en contact partiel avec la surface du composant testé. Les causes peuvent être nombreuses, par ex : un mauvais nettoyage de la surface de collage ou une manipulation inappropriée de la surface d'application et de l'adhésif. Ces causes doivent et peuvent être évitées. Le test de la gomme à effacer en caoutchouc clarifie généralement la situation. Bien qu'il puisse être possible de se passer de la protection des points de mesure pour une mesure à court terme (essai de traction), l'installation des jauges de contrainte requiert toutefois une approche consciencieuse et fréquemment une bonne expérience. Il n'y a probablement aucune autre méthode de mesure dans laquelle la connaissance et l'expérience de la personne effectuant la tâche jouent un rôle si important. C'est pourquoi les entreprises et les instituts profitent de plus en plus fréquemment de la possibilité de certifier leur personnel selon la norme VDI/VDE/GESA 2636 avec divers niveaux de qualification.