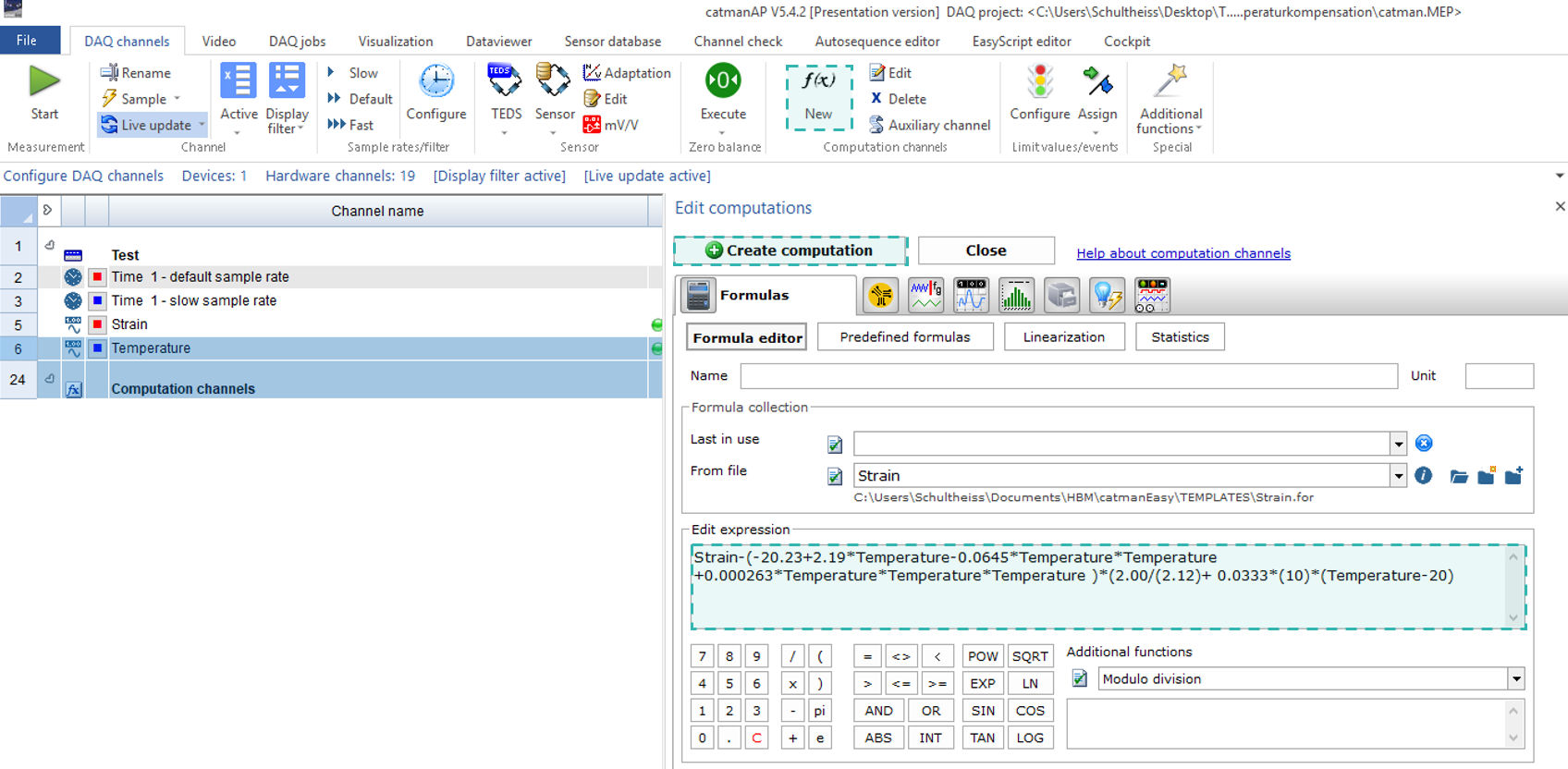
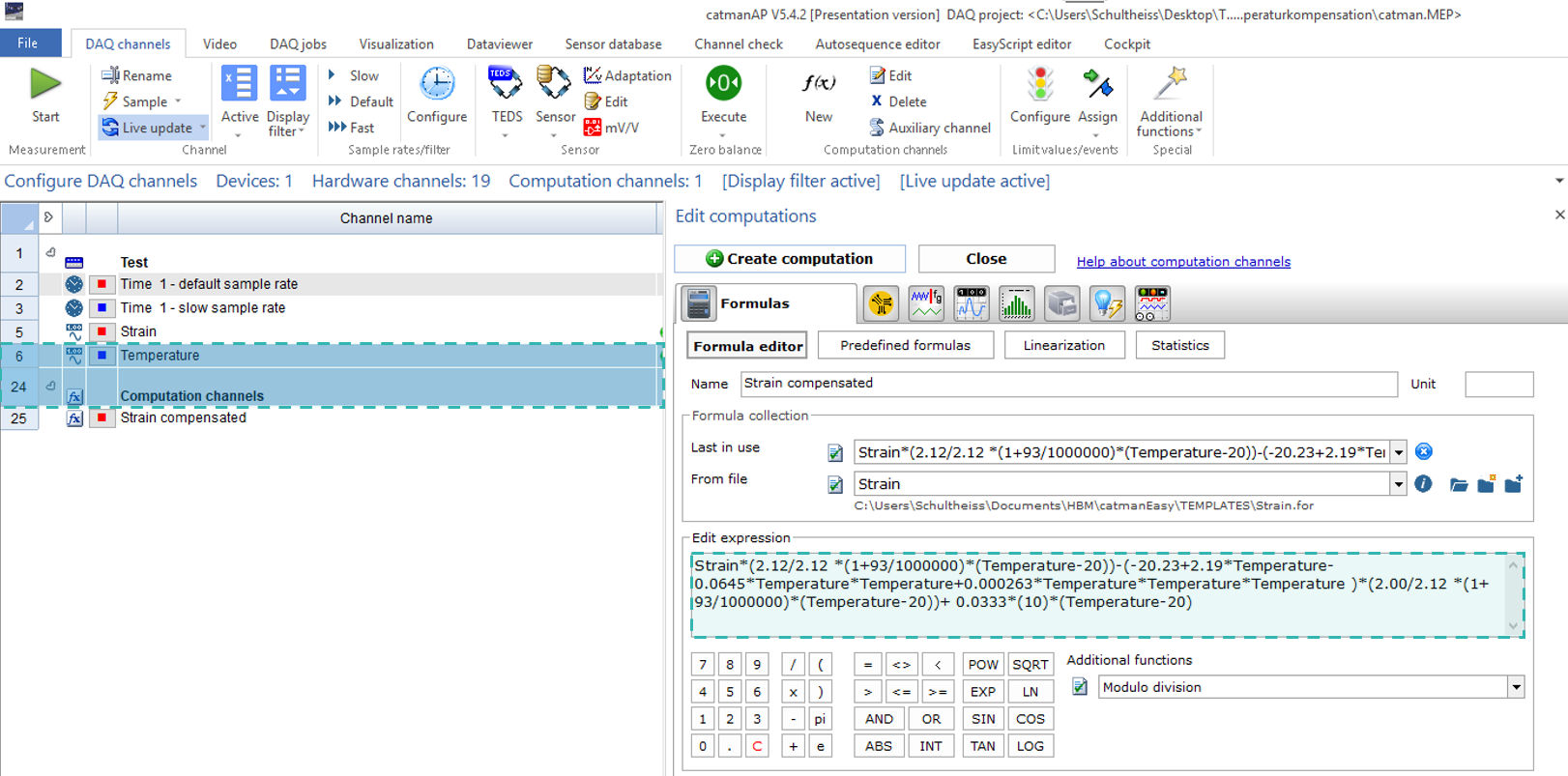
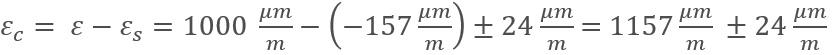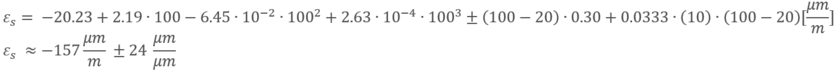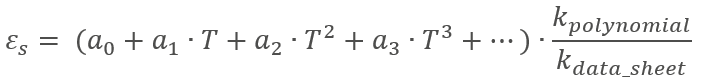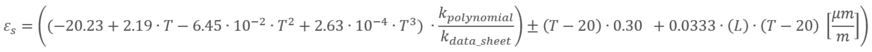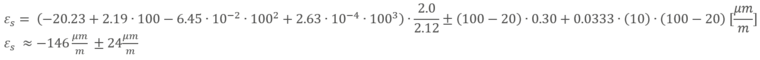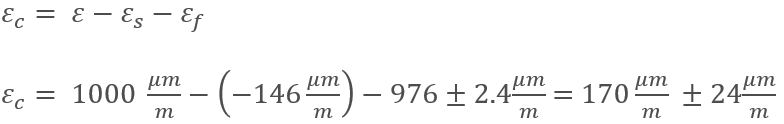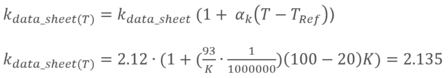In some cases, the polynomial includes further contributors that influence the strain signal if the temperature changes:
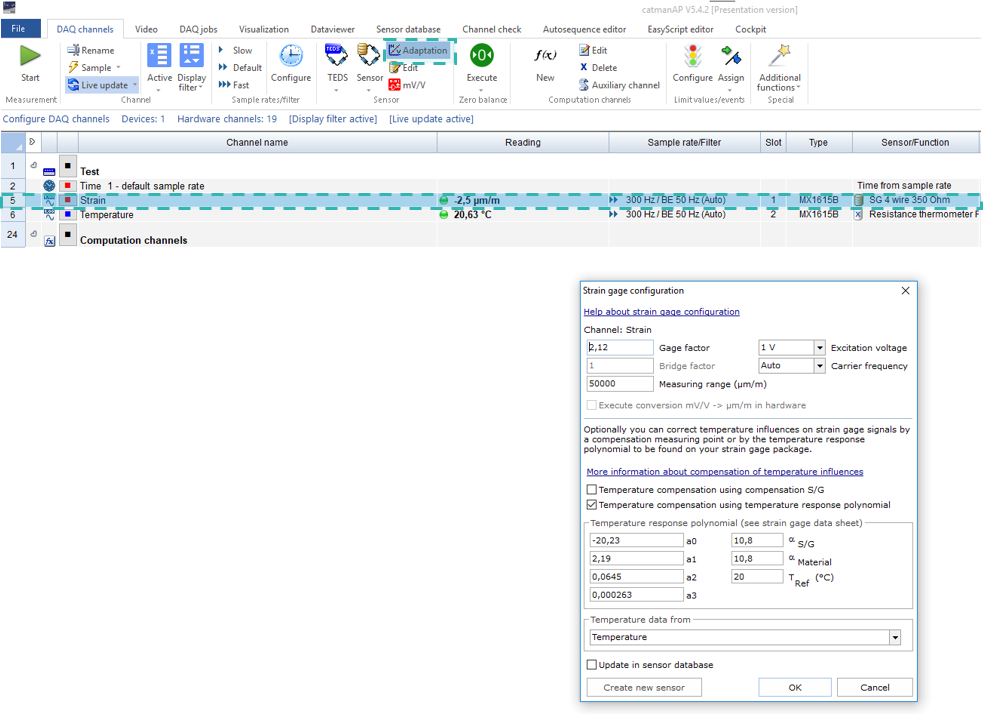
- Influence of leads (εl): In this specific example the measurement uncertainty and the influence of 2-wire strain gauge leads connected to the measurement grid is added as well. Generally, the influence of leads must be considered as well, but it might differ between gauge types and manufacturers. If you are using our HBM-patented 3- or 4-wire technology this compensates all cable resistances, but in some cases, there is a residual 2-wire part which cannot be compensated automatically.
- Measurement Uncertainty (εu): The measurement uncertainty is a general part which should be considered in the total calculation. Even the polynomial has some scatter which leads to this uncertainty part.
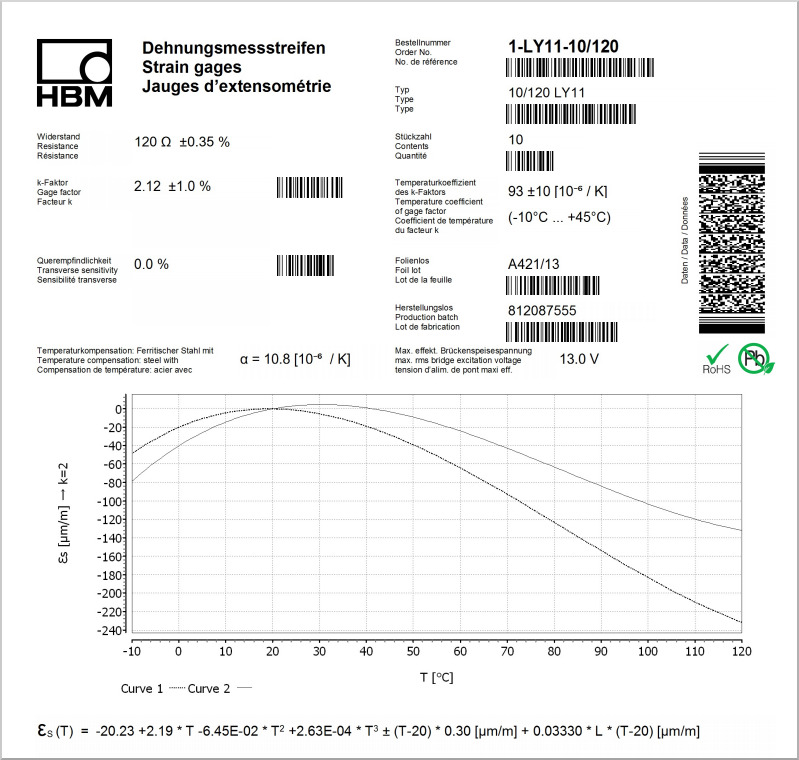
The adapted polynomial is as follows:
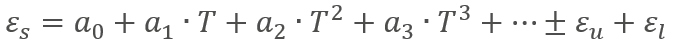
Focusing on our application example it looks like:

Let’s assume that the temperature during the strain measurement is constantly 100 °C (T = 100 °C) and the length of leads is 10 mm (L = 10 mm). Please be aware that the length of leads can vary. Looking at the polynomial, it demonstrates that the thermal strain has a significant impact on the result, since it is higher than 100 μm/m!
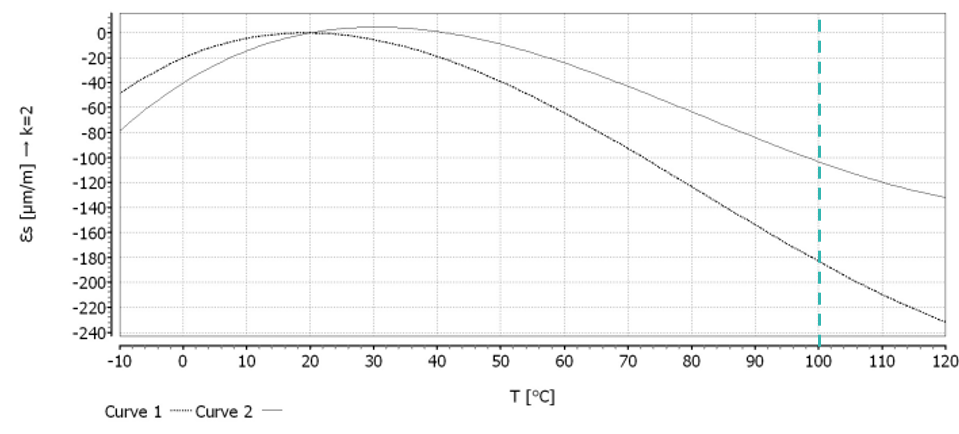
To calculate the thermal output strain, deploy the temperature and the length of leads into the polynomial:
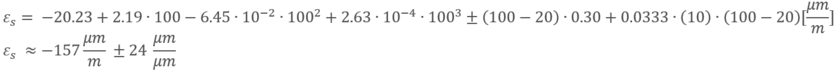
The result fits quite well to the polynomial displayed on the data sheet. By considering the polynomial the most significant influences are taken into account, whereas only very long 2-wire cables can impact the result additionally. Since we use the 3- and 4-wire technology that compensates the impact of cable resistance, this part of the calculation is not relevant!
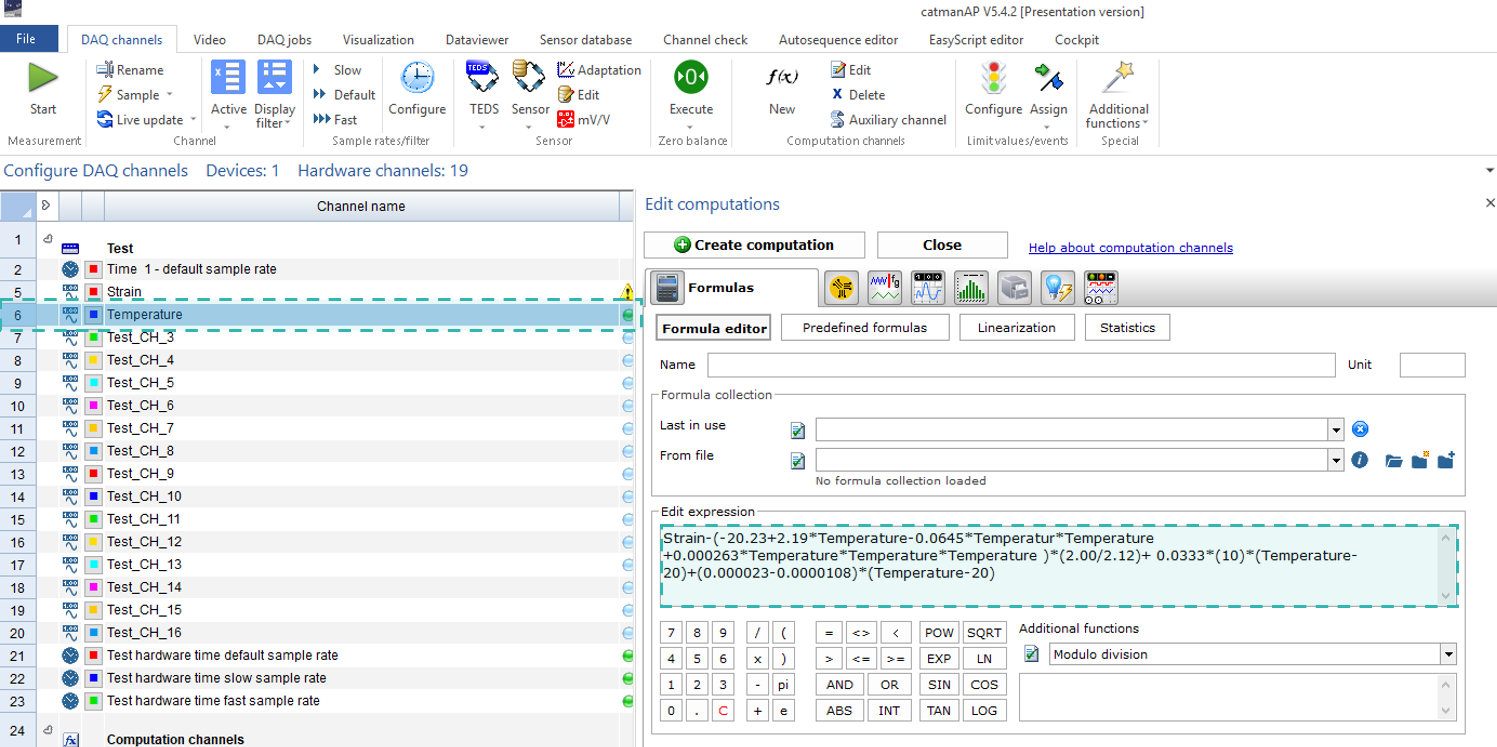
Superimposing the thermal strain on the measured strain now gives the corrected strain value, which only takes the mechanical strain into account: