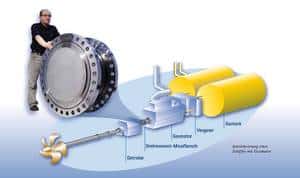
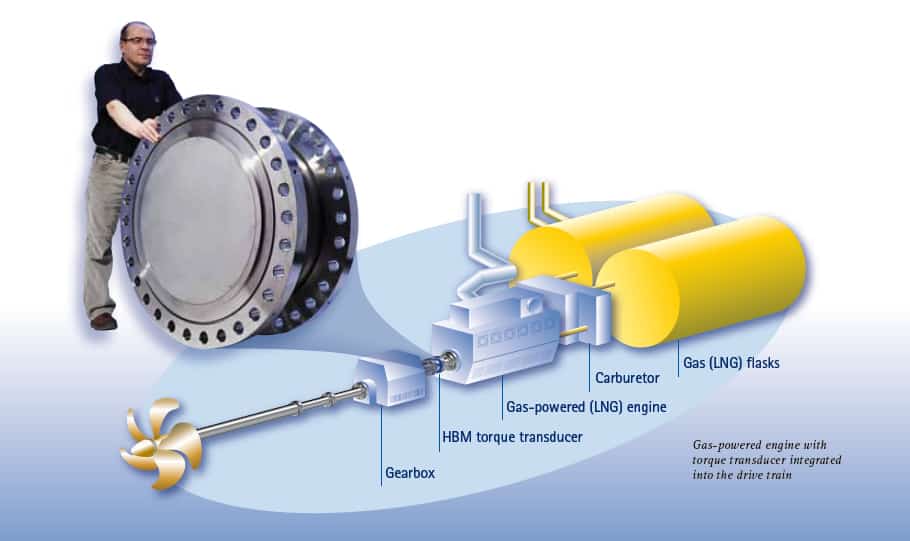
Misurazione della potenza su grandi propulsori con motori a combustione
1. Rilevazione del segnale di potenza
I moderni concetti di propulsione con grandi motori a combustione, richiedono la risposta precisa e veloce dei sistemi di controllo del motore (p. es. alimentazione del carburante) per reagire alle brusche variazioni di carico. Infatti, è essenziale garantire che venga fornita sufficiente potenza in qualsiasi momento e, che nel contempo, il motore abbia un basso consumo di carburante e sicuri parametri operativi. Ciò richiede che venga fornito un segnale di potenza che - insieme ai sistemi del veicolo, del compressore e della pompa - deve essere generato utilizzando speciali apparati di misura. In generale, esistono tre metodi diversi:
- Il segnale di potenza viene rilevato indirettamente misurando specifiche grandezze ausiliarie quali la portata, la temperatura e la pressione, da cui calcolare la potenza. Con questo metodo l'incertezza di misura del segnale di potenza è molto elevata. Un ulteriore inconveniente è che i valori delle grandezze ausiliarie non sono sincroni ai processi che determinano la potenza del motore.
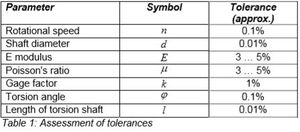
- Il segnale di potenza viene rilevato indirettamente misurando specifiche grandezze ausiliarie sull'albero d'ingresso. Ciò comprende tutti i metodi che implichino sia la misurazione della deformazione superficiale risultante dalla torsione dell'albero che l'angolo di torsione dell'albero. In ambedue i casi, la potenza viene calcolata dopo la misurazione delle grandezze ausiliarie.
- Il segnale di potenza viene rilevato direttamente misurando la coppia sull'albero di ingresso.
Il seguente articolo confronta il metodo di misurazione diretta della potenza con quello di misurazione indiretta, rispettivamente sul e nel treno di trasmissione (metodi b. et c.), per quanto concerne le incertezze di misura che possono essere ottenute.
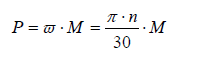 (1)
(1)
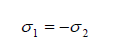 (3)
(3)
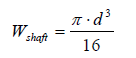 (5)
(5)
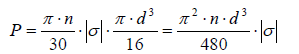 (6)
(6)
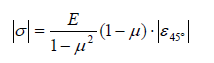 (7)
(7)
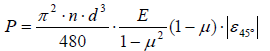 (8)
(8)
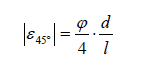 (9)
(9)
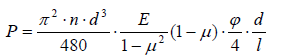 (10)
(10)