統計的な手法を使用して疲労解析用のフィールド試験データを検証する
この論文では、計測データの取得に関するいくつかの統計的な手法について説明します。また、さらに長時間にわたってデータを収集した場合に予想される時刻歴、その結果の疲労損傷がどの程度になるかを推定します。
要約
試験エンジニアは、現場での試験中、特定の業務を特徴付けるのに十分なデータがいつ収集されたのかを決定しなければならない場 面に直面します。この論文では、計測データの取得に関するいくつかの統計的な手法について説明し、さらに長時間にわたってデータを収集した場合に予想され る時刻歴、およびその結果の疲労損傷がどの程度になるかを推定します。実際の計測値と推測される時刻歴範囲の両方から疲労損傷を計算した時に、十分なデー タが収集されます。
背景
車両や構造体の設計において重要な要素は、その用途において予想される使用条件の過酷さです。新しい車両の場合、用途が不明で あるため、短時間の試験を頻繁に行って構造体に作用する荷重とその結果としての応力を決定します。ある車両の荷重履歴には、しばしば確定的な部分と無作為 の部分の両方が含まれています。例えばダンプトラックは、荷物を積んだ状態と空の状態の確定的な負荷サイクルを持っている可能性がありますが、これには 様々な路面上を運転したことによる一連の無作為な荷重が組み合わせられています。負荷サイクル荷重は、同時に事実上の変数でありながら運転荷重とは異なる 母集団からのものであると見なされる場合があります。すべての試験エンジニアが直面する問題は、特定の用途条件を特徴付けるのに十分なデータが収集された のは、どの時点なのかを決定することです。
図1は、試験トラック上を走行しているオフロード車の前輪サスペンション荷重を対象として計測された現場荷重履歴を示します。履歴は10周で記録されています。

図1:試験トラック上での10周
慎重に制御された試験用トラックで一人のドライバーが運転しているにもかかわらず、この図では周回ごとの荷重変動を容易に理解することができます。
疲労損傷の観点から見て、図1に示されたデータは、このコンポーネントに期待される寿命に対応した用途を特徴付けるのに十分で しょうか?この質問に対する答えは、計測された荷重履歴の変動を使用して、より長時間にわたって荷重を計測した場合に予想される疲労損傷と荷重履歴がどの 程度になるかを推定することによって得られます。
荷重と時間の関数に使用することを目的として時間領域における変動性を解析することは、不適切、あるいは不必要です。疲労においては、荷重履歴そのものよりも、荷重のレインフローヒストグラムの方が(そこから疲労損傷を計算したため)より興味を引きます。
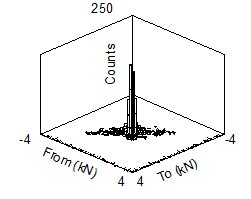
図2:レインフローヒストグラム
二次元のレインフローヒストグラムには、荷重の範囲と平均の両方に関する情報が含まれています。図2は、To-From形式の 図1から得たデータのレインフローヒストグラムを示しています。このタイプのヒストグラムでは平均応力のもたらす影響が保存されますが、これは一般に疲労 の解析にとって重要な点です。
図2からのデータを、累積超過ダイアグラムとしてプロットしたのが図3です。
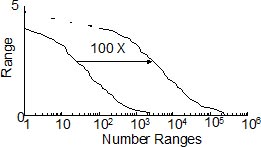
図3:超過ダイアグラム
グラフの左側に示されている曲線が、元の荷重履歴の超過曲線です。1,000周分の試験データを計測した場合(100倍の長 さ)には、この分布が右に移動して同様の形状を示すと予想されます。破線は、時間が長くなった場合に予想される高い荷重を図示したものです。超過ダイアグ ラムは容易に視覚化できますが、平均効果に関する有益な情報が失われます。
この論文では、計測したレインフローヒストグラムにおける変動性を使用して、より長い時間で予想されるレインフローヒストグラ ムを推測する方法を示します。その結果、この外挿されたヒストグラムを使用して、試験または解析に使用する目的で新しい長時間の履歴を再構築することがで きます。
レインフロー外挿法
レインフローヒストグラムの外挿を最初に提案したのはDresslerでした[1]。ここでは、その概念を簡単に説明します。 詳細については、参考資料1を参照してください。レインフローヒストグラムは、二次元の確率分布として扱います。ヒストグラムのそれぞれのビン(箱)に含 まれるサイクルの回数をサイクルの総数で割ることにより、単純な確立密度関数が得られます。発生可能性にしたがってヒストグラム内のサイクルを無作為に配 置することにより、あらゆる数の総サイクルに対応する新しいヒストグラムを構築することができます。一方、このアプローチはヒストグラム内のサイクルに外 挿因子を掛けることと基本的に同じです。しかしこれは現実的ではありません。たとえ同じドライバーが同じ試験トラック上を走っても、同じ荷重履歴を繰り返 すことは不可能です。例えば、ドライバーが路上にできた穴を通過する度に荷重には何らかの相違が生じます。図1では、この点が明確に示されています。特定 のイベントからのピーク荷重は、レインフローヒストグラム内にある特定のビンの中に配置されます。その後の周回中に、この荷重は異なる最大値を持つことに なり、最初の周回に隣接する同じグループのビン内に配置されます。
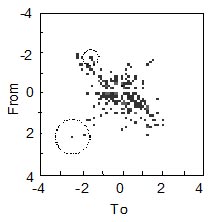
図4:ヒストグラムの変動性
図4は、レインフローヒストグラムを平面像で示したものです。ここでは2から-2.5まで続くイベントを考えます。次にこのイ ベントが繰り返される時には、大きな破線の円形で示した座標(2、-2.5)近辺のどこかになるはずです。ヒストグラムのこの領域にはデータが少なく、か なり大きな変動性があると推察されます。次に、-2から-1.5までの円形を考えます。ここには遥かに多くのデータがあり、したがって変動性はずっと小さ く、小さな破線の円で示した大きさになると思われます。レインフローヒストグラムを外挿することは、基本的に元のレインフローデータから二次元の確率分布 関数を見つけ出す作業です。
連続的な母集団、Xから取得したある一組のデータについて、データの確率分布を構築するには多くの方法があります。確率密度予 測には、一般的にパラメータと非パラメータの2種類があります。パラメータによる密度予測では、与えられたデータセットが予め確定済みの理論的な確率分布 にフィットするという仮定が立てられます。分布に使用する形状パラメータは、このデータから推測しなければなりません。一方、非パラメータの密度予測で は、データセット全体の分布について仮定を立てることはありません。ヒストグラムは、非パラメータの密度推定量です。外挿の目的では、ヒストグラムの不連 続ポイントを、連続した確率密度に変換したいと考えます。カーネル密度推定量[2-3]は、確率分布を推測するための便利な方法を提供してくれます。この 方法では、仮定した確率分布をヒストグラムの局所領域にフィットさせることだと見なします。この局所領域のサイズは、推定量の帯域幅によって決まります。 図4内に表示した円によってそのサイズを示します。カーネル密度に使用する適応帯域幅は、検討対象となるポイントの近傍にどれほど多くのデータがあるかに よって決まります。
データが多数存在するヒストグラムの領域については、統計的な方法が十分に開発されています。しかし、データの少ない領域に対 しては特別な配慮が必要です[4]。外挿されたヒストグラムにおいて予想される最大荷重の範囲は、大きな荷重範囲に至るまで、ワイブルフィットから予測す ることができます。次に、この予測を使用してヒストグラム内のデータが少ない領域における適応帯域幅を決定します。この適応帯域幅が決まると、ヒストグラ ム全体の分布密度を計算することが可能になります。適切な確率でヒストグラム内にサイクルを無作為に配置することにより、希望するサイクルの総数に対して 予想されるヒストグラムを構築します。このプロセスでは、一意的な外挿は生成されない点に留意する必要があります。同じ外挿因子を使用して多くの外挿を実 行することが可能であり、これにより結果的な荷重履歴の変動性に関してかなりの情報を取得することができます。
荷重履歴の外挿を1,000回行った結果を図5に示します。外挿の結果を図6に示した超過ダイアグラムの観点から見ると、より 容易に視覚化することができます。この図では2つのプロットを示しています。一方は図5のデータからのもので、もう一方は元の荷重履歴を1,000回繰り 返した結果を示します。
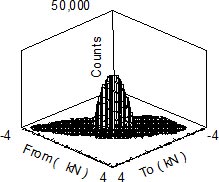
図5:外挿されたヒストグラム
表1は、元の荷重履歴の様々な外挿から計算した疲労寿命の結果を示しています。疲労寿命は、構造体の予想使用寿命を時間単位で 表したものです。計算で使用されているのは、単純なSNアプローチです。便利な疲労解析方法であればどれでも使用可能で、材料特性の確率論的記述と組み合 わせることができます。
表1:疲労寿命
荷重履歴 | 寿命 | 最大 | 最小 |
|---|---|---|---|
元の履歴 | 29,890 | 1.89 | -2.12 |
10回 | 26,760 | 2.25 | -2.50 |
100回 | 16,170 | 2.88 | -3.25 |
1000回 | 10,190 | 3.25 | -3.63 |
予想したように、計算によって得られた疲労寿命は、荷重履歴が長くなるとより低くなります。これは、外挿されたヒストグラムでは荷重がより大きいからです。しかし、荷重が大きいことは、その構造体の耐用年数全体を通した運転荷重のより現実的な予測を意味します。
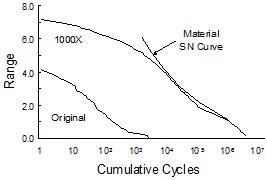
図6:サイクルおよび疲労損傷の分布
損傷サイクルを効果的に視覚化する方法の一つとして、図6に示すように、サイクルの分布と材料の挙動を同一スケール上にプロッ トする方法があります。材料特性のスケールを荷重履歴と同じ単位になるように調整することで、このプロットは一定の大きさの荷重条件において予想される疲 労寿命を表します。2曲線の接触点が、最も損傷が大きなサイクルの範囲を示します。この履歴では、最大荷重範囲サイクルが最も損傷が大きいサイクルになっ ておらず、この荷重履歴における最も損傷が大きなサイクルは、外挿されたヒストグラム上では、最大荷重範囲の約半分になっています。
レインフロー再構築
レインフロー再構築の目的は、元のレインフローヒストグラムと同様の疲労損傷を持つ時刻歴を取得することです[5]。基本的に は、過去にさかのぼって計数しながらレインフローを実行するのが希望です。レインフローヒストグラムから始めて、同じレインフローカウントを持つ時刻歴 を、サイクルごとに再構築します。ヒストグラム内で全体として最大のサイクルはすでに判明しています。To-From形式では、レインフロー計数は、 Peak-Valley-Peak(PV、山-谷-山)サイクルとValley-Peak-Valley(VP、谷-山-谷)サイクルの差異を明確に区別 します。VPサイクルは、ヒストグラムの主対角線の上側に保存され、PVサイクルは下側に保存されます。いずれのVPサイクルにおいても、ヒストグラムの 行は列よりも少なくなっています。同様に、PVサイクルにおいては、ヒストグラムの列は行よりも少なくなっています。VPサイクルを挿入するプロセスを図 7に示します。左側の数字がヒストグラムのビン、行、あるいは列を示しており、これらは結果として得られる荷重履歴の大きさに比例します。再構築された時 刻歴はPとVで示され、挿入されるサイクルはr(行)とc(列)として示されます。
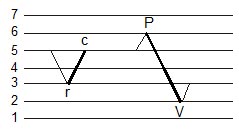
図7:VPサイクルを挿入する
VPサイクル(r<c)は、c≦Pかつr>Vの場合、いずれのPV反転サイクルにも挿入することができます。VPサイクルは同じ大きさのPVサイクルには挿入できません。
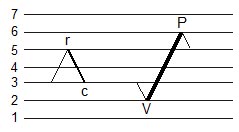
図8:PVサイクルを挿入する
図8は、PVサイクルの挿入を示します。PVサイクル(c<r)は、r<Pかつc≧Vの場合、いずれのVP反転サイクルにも挿入することができます。PVサイクルは同じ大きさのVPサイクルには挿入できません。
上述した2つの単純な規則が、レインフロー再構築のための基本となります。再構築のプロセスは、PVPまたはVPVのどちらか で、最大のサイクルから始まります。次に、2番目に大きなサイクルが再構築された時刻歴の適切な位置に挿入されます。最初の数サイクルを経過した後には、 より小さなサイクルを挿入することが可能な場所が数多く出てきます。挿入可能なすべての場所が決まると、そのうち1個が無作為に選択されます。
要約
車両や構造体の耐久性は、その耐用年数の全期間を通じて荷重の分布による影響を受けます。ここまでは短期的な計測荷重から長期的な耐久性を推定するための手法について説明してきました。
参考文献
[1] Dressler, K, B. Grunder, M. Hack and V.B. Koettgen, "Extrapolation of rainflow matrices", SAE Paper 960569, 1996
[2] Silverman, B.W. "Density estimation for statistics and data analysis" Chapman and Hall, New York, 1986
[3] Scott, D.W. "Multivariate density estimation" Wiley, New York, 1992
[4] Roth, J.S. "Statistical modeling of rainflow histograms" Materials Engineering-Mechanical Behavior Report No. 182, UILU-ENG 98-4017, University of Illinois, 1998
[5] Khosrovaneh, A.K. and N.E. Dowling, "Fatigue loading history reconstruction based on the rainflow technique", International Journal of Fatigue, Vol. 12, No. 2, 1990, 99-106