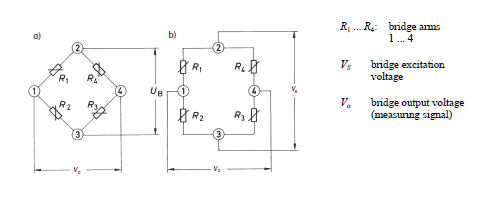
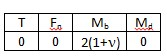
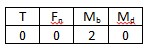
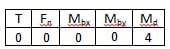
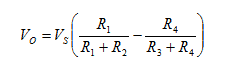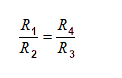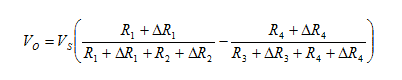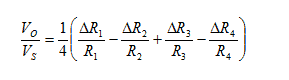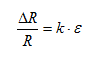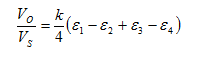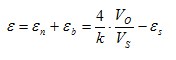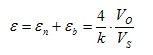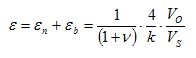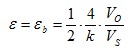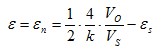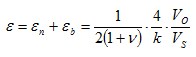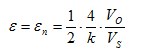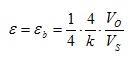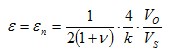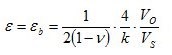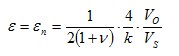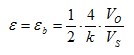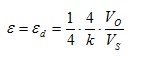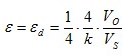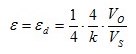| | Bridge configuration | External impacts measured: | Application | Description | Advantages and disadvantages |
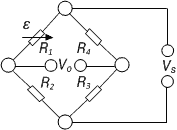
| 1 | 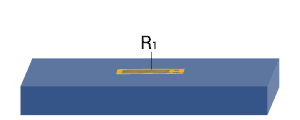
| 
| 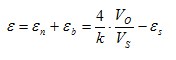
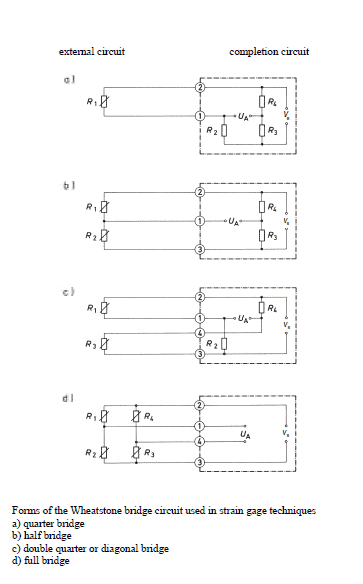
| Strain measurement on a tension/ compression bar
Strain measurement on a bending beam | Simple quarter bridge
Simple quarter bridge circuit with one active strain gauge | + Easy installation
- Normal and bending strain are superimposed
- Temperature effects not automatically compensated |
| 2 | 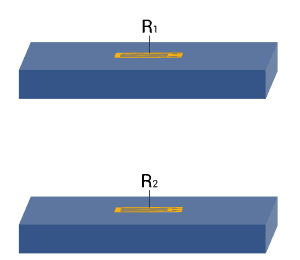 | 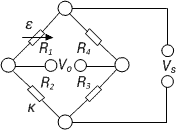
| 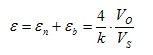
| Strain measurement on a tension/ compression bar
Strain measurement on a bending beam | Quarter bridge with an external dummy strain gauge
Two quarter bridge circuits, one actively measures strain, the other is mounted on a passive component made of the same material, which is not strained | + Temperature effects are well compensated
- Normal and bending strain cannot be separated (superimposed bending) |
| 3 | 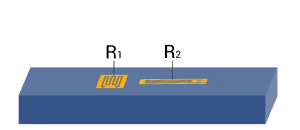
| 
| 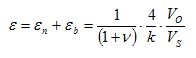

| Strain measurement on a tension/ compression bar
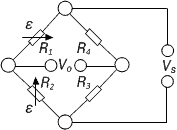
Strain measurement on a bending beam | Poisson half-bridge
Two active strain gauges connected as a half bridge, one of them positioned at 90° to the other | + Temperature effects are well compensated when material is isotrop |
| 4 | 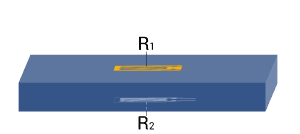
| 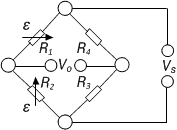
| 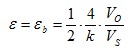
| Strain measurement on a bending beam | Half bridge
Two strain gauges are installed on opposite sides of the structure | + Temperature effects are well compensated
+ Separation of normal and bending strain (only the bending effect is measured) |
| 5 | 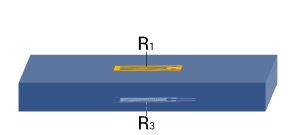
| 
| 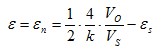
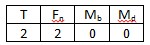
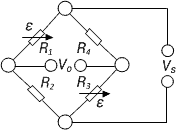
| Strain measurement on a tension/ compression bar | Diagonal bridge
Two strain gauges are installed on opposite sides of the structure | + Normal strain is measured independently of bending strain (bending is excluded) |
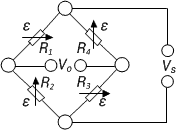
| 6 | 
| 
| 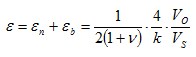
| Strain measurement on a tension/ compression bar
Strain measurement on a bending beam | Full bridge
4 strain gauges are installed on one side of the structure as a full bridge | + Temperature effects are well compensated
+ High output signal and excellent common mode rejection (CMR)
- Normal and bending strain cannot be separated (superimposed bending) |
| 7 | 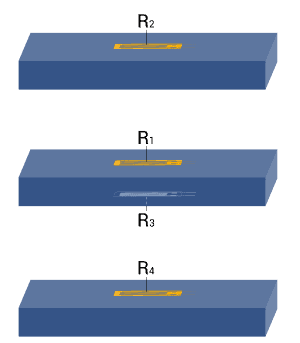 | 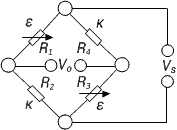
| 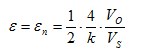
| Strain measurement on a tension/ compression bar | Diagonal bridge with dummy gauges
Two active strain gauges, two passive strain gauges | + Normal strain is measured independently of bending strain (bending is excluded)
+ Temperature effects are well compensated |
| 8 | 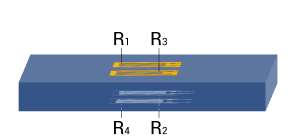
| 
| 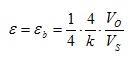
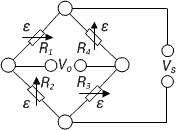
| Strain measurement on a bending beam | Full bridge
Four active strain gauges are connected as a full bridge | + Separation of normal and bending strain (only the bending effect is measured)
+ High output signal and excellent common mode rejection (CMR)
+Temperature effects are well compensated |
| 9 | 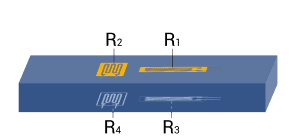
| 
| 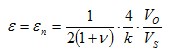

| Strain measurement on a tension/ compression bar | Full bridge
Four active strain gauges, two of them rotated by 90° | + Normal strain is measured independently of bending strain (bending is excluded)
+ Temperature effects are well compensated
+ High output signal and excellent common mode rejection (CMR) |
| 10 | 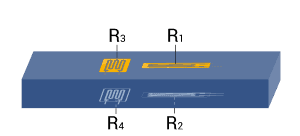
| 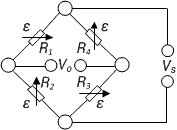
| 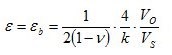
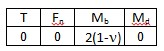
| Strain measurement on a bending beam | Full bridge
Four active strain gauges, two of them rotated by 90° | + Separation of normal and bending strain (only the bending effect is measured)
+ Excellent common mode rejection (CMR)
+ Temperature effects are well compensated |
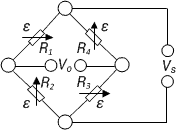
| 11 | 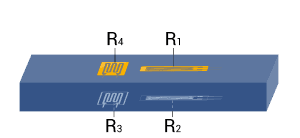
| 
| 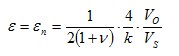
| Strain measurement on a bending beam | Full bridge
Four active strain gauges, two of them rotated by 90° | + Separation of normal and bending strain (only the bending effect is measured)
+ High output signal and excellent common mode rejection (CMR)
+ Temperature effects are well compensated |
| 12 | 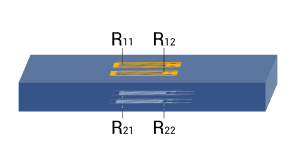
| 
| 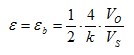
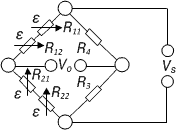
| Strain measurement on a bending beam | Half bridge
Four active strain gauges connected as a half bridge | + Separation of normal and bending strain (only the bending effect is measured)
+ Temperature effects are well compensated
+ High output signal and excellent common mode rejection (CMR) |
| 13 | 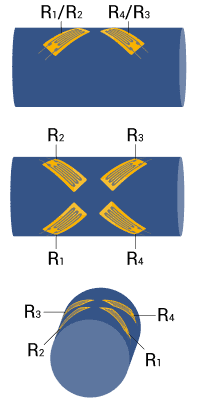 | 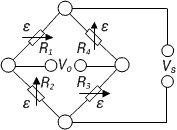
| 
| Measurement of torsion strain | Full bridge
Four strain gauges are installed, each at an angle of 45° to the main axis as shown | + High output signal and excellent common mode rejection (CMR)
+ Temperature effects are well compensated |
| 14 | 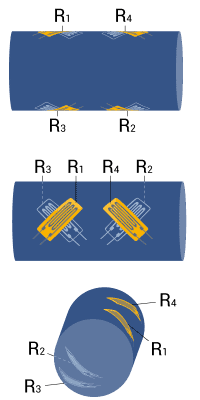 | 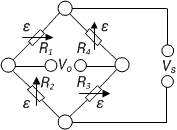
| 
| Measurement of torsion strain with limited space for installation | Full bridge
Four strain gauges are installed as a full bridge, at an angle of 45° and superimposed (stacked rosettes) | + High output signal and excellent common mode rejection (CMR)
+ Temperature effects are well compensated |
| 15 | 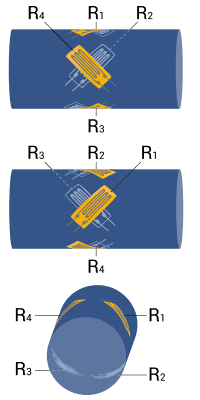 | 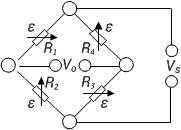
| 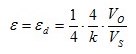
| Measurement of torsion strain with limited space for installation | Full bridge
Four strain gauges are installed as a full bridge at an angle of 45° and superimposed (stacked rosettes) | + High output signal and excellent common mode rejection (CMR)
+ Temperature effects are well compensated |