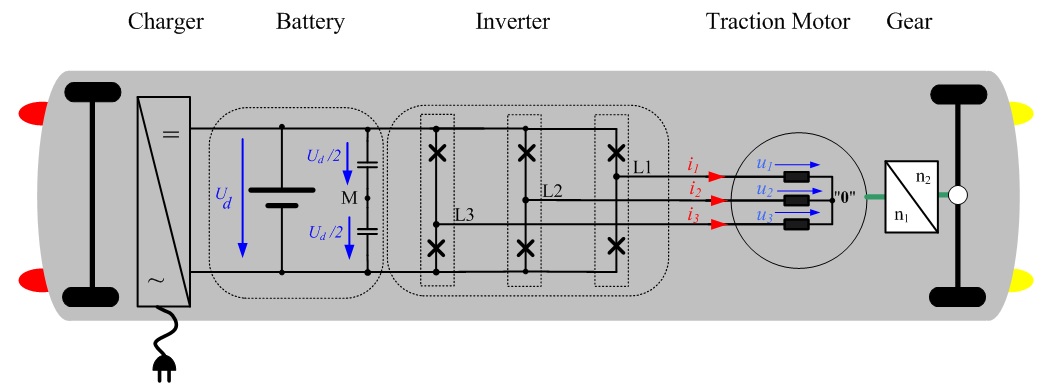
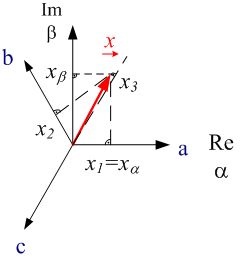
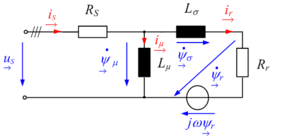
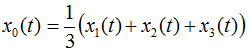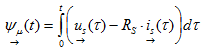그림. 3.1은 인버터 구동 비동기식 모터의 상전압 (u1(t),u2(t),u3(t))과 상전류 (i1(t),i2(t),i3(t))를 나타냅니다. 전류와 전압의 계산 방향은 그림 1.1의 개요에 나와 있습니다. 공간벡터의 양은 방정식 2.02로 계측된 상의 양으로 산출될 수 있습니다. Perception에서 모든 변수는 모두 실수이어야 하기 때문에 공간벡터의 실수부와 허수부는 개별적으로 산출됩니다. 다음 방정식은 상전압과 상전류 계산식입니다.
(3.01)
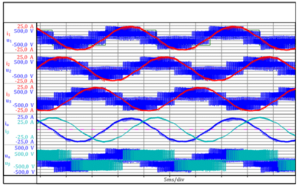
그림. 3.1: 계측된 상의 양 (i1,i2,i3,u1,u2,u3)과 계산된 공간벡터의 양 (ia,ib,ua,ub) (Perception 사용자들을 위해 이 계측 값은 다음의 파일 0 공간벡터와 에어 갭 토크 pNRF-에서 사용 가능합니다.. HBM웹사이트에서 이 파일을 다운로드하여 사용하세요).
비동기식 모터의 고정자 자속 계산
고정자 자속 공간벡터는  비동기식 모터의 자기장을 설명하고, 모터의 고정자 저항 Rs의 고정자 전압과 전압 강하 간의 차이를 적분해 구합니다.
비동기식 모터의 자기장을 설명하고, 모터의 고정자 저항 Rs의 고정자 전압과 전압 강하 간의 차이를 적분해 구합니다.
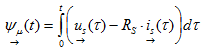
(3.06)
정확도 요건에 따라 일부 모터에서 낮은 고정자 저항은 종종 무시될 수 있습니다. 적분 결과, 고정자 자속은 연속적인 양입니다. 그림 3.1와 같이 고정자 전압이 펄스 폭 변조 반응을 보여주고 있어도, 고정자 자속 공간벡터의 실수부 ψα(t) 와 허수부 ψβ(t) 는 대략 사인곡선 (그림 3.2a)임을 알 수 있습니다.. 대략적인 근사치로서 고정자 자속 공간벡터의 상각궤도는 원호를 따라갑니다. 원호의 반경은 고정자 자속의 진폭과 일치합니다.
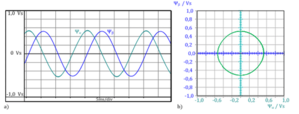
그림 3.2: 비동기식 모터의 고정자 자속 공간벡터
a) 실수부와 허수부의 시간 반응
b) 복소 평면의 공간벡터의 상각궤도
인버터 구동 비동기식 모터의 내부 에어 갭 모멘트 계산
비동기식 모터에서 소위 내부 또는 에어 갭 모멘트를 전압이나 자속 및 전류 계측을 통해 산출할 수 있습니다. 내부 에어 갭 모멘트는 모터 내부의 불가피한 마찰 토크와 축의 토크로 구성되어 있습니다. 마찰 토크를 무시하면 계산된 내부 토크는 토크 트랜스듀서로 아주 정확하게 계측 가능한 기계적 토크와 일치합니다[3].
계산된 토크의 정확도는 사용한 산정 모델과 모터 매개변수의 정확도에 따라 다릅니다. 내부 토크의 계산은 그것의 양이 최소한 기계적 모멘트와 동일한 계산 차수에 있어야 하기 때문에 토크 트랜스듀서의 계측 신호를 보완하는 중복 정보로 사용될 수 있습니다. 게다가, 전기 모터의 비례식 토크는 토크 트랜스듀서로 계측된 전체 구동렬의 토크와 상호 연관될 수 있습니다. 가령, 그것의 연소 기관과 전기 자동차의 모터가 동일한 구동렬 상에 작동하기 때문에 잠재적 어플리케이션으로 하이브리드 자동차를 들 수 있는데, 전기 모터의 토크를 계산하여 그 연소 기관의 모멘트를 결정할 수 있습니다.
비동기식 모터의 내부 토크는 고정자 전류와 자기 고정자 자속으로 계산될 수 있다는 점은 문헌[2]에 잘 알려진 사실입니다.
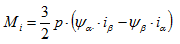
(3.06)
여기서, ρ 는 비동기식 모터의 풀 페어 수를 나타내며, 전류와 자속은 그것의 공간벡터 요소로 표현됩니다. 그림. 3.3은 고정자 전류와 그 자속의 시간 반응뿐만 아니라 이 값으로 계산된 내부 에어 갭 모멘트Mi 을 보여줍니다. 그 결과로 발생한 토크 리플이 뚜렷이 가시화됩니다. 고주파 토크 리플은 인버터의 개폐 동작의 결과로 발생됩니다. 한편, Perception 소프트웨어로 에어 갭 모멘트를 계산하려면 모터 전류의 기본파 주기를 정확히 확인해야 합니다.
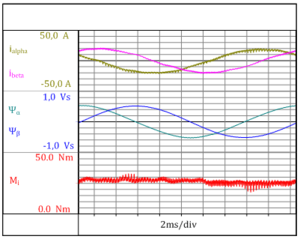
그림. 3.3: 고정자 전류(iα, iβ), 고정자 자속 (ψα, ψβ) 및 계산된 에어 갭 모멘트 Mi 의 시간 반응