Calculando Grandezas Vetoriais Espaciais e Torque no Entreferro de Motores de Indução CA Alimentados por Inversores Usando Genesis HighSpeed e Software Perception

Devido ao seu design simples e robusto, motores de indução CA alimentados por inversores são muitas vezes utilizados em unidades de tração. A fig. 2.1 mostra um motor de indução CA alimentado por inversores do tipo gaiola. O estator fixo tem três enrolamentos. A gaiola é projetada com barras de alumínio ou de cobre e é curto-circuitada com anéis condutores nas extremidades do motor.

Aplicando três correntes deslocadas no tempo para os enrolamentos espacialmente compensados produz um campo magnético rotativo. O campo magnético gira com a velocidade de rotação síncrona de:

(2.01)

A equação 2.01 mostra que a velocidade de rotação síncrona depende da frequência da corrente do estator f_S  e o chamado o número de pares de pólos p do motor de indução CA alimentados por inversor.

O campo magnético atravessa o rotor do tipo gaiola. Este movimento induz tensões nas barras condutoras. Devido aos anéis de aperto nas extremidades do rotor, as grandes correntes resultantes da tensão induzida fluem nas barras. De acordo com a lei de Lenz, as forças que são produzidas aceleram o rotor no sentido do campo rotativo. Isto reduz a diferença na velocidade de rotação entre o rotor e o campo rotativo.

Fig. 2.1: estrutura de um motor de indução CA alimentados por inversor com rotor do tipo gaiola

a) Seção transversal e b) seção longitudinal do motor

Vetores Espaciais

Em 1959, Kovacs desenvolveu a teoria do vetor espacial para facilitar a descrição matemática de sistemas trifásicos. Ele é frequentemente usado na prática para descrever os métodos de controle de motores de indução AC alimentados por inversores. Os parâmetros elétricos e magnéticos de um sistema de três fases pode ser mapeado num sistema de duas fases, ortogonal e em um sistema de sequências de zero, que está presente em determinadas circunstâncias. O sistema de duas fases, ortogonal pode ser interpretado como um número complexo chamado de vetor espacial. A sua parte real e imaginária corresponde as projeções do número complexo, exibido como um vetor, nos eixos α e β no plano complexo. A equação 2.02 define as regras de cálculo para o vetor espacial complexo das três grandezas de fase x₁, x₂  e x₃ .

(2.02)

com α sendo um operador complexo. O sistema de sequências de zero associado é calculado como se segue:

(2.03)

A figura 2.2 mostra vetor espacial no sistema de coordenadas ortogonal. A parte real do vetor espacial é plotado na abscissa α e a parte imaginária na ordenada β. Os valores de fase são obtidos através da projeção do vetor espacial sobre os eixos a,b,c rotacionados em 120°.

Fig. 2.2: Vetores espaciais no plano complexo

Diagrama de circuito equivalente de um motor de indução CA alimentado por inversor usando vetores espaciais

O comportamento operacional dos motores elétricos é muitas vezes descrito por diagramas de circuitos equivalentes. A Fig. 2.3 mostra o diagrama de circuito equivalente simplificado de um motor de indução CA alimentados por inversor usando vetores espaciais. A tensão do estator aplicada ao motor de indução CA alimentado por inversor é descrita pelo vetor espacial. A corrente do estator flui para o motor de indução CA alimentado por inversor. No diagrama de circuito equivalente, a resistência do estator é representado por R_s. A indutância L_μ é a magnetização de indutância do motor. A indutância de fuga do motor é combinada em L_σ. R_y designa a resistência do rotor convertido para o lado do estator. A velocidade de rotação mecânica n no eixo do motor de indução CA alimentado por inversor é contabilizado no diagrama de circuito equivalente através da freqüência angular eletromecânica ω. Estas duas grandezas podem ser convertidas umas nas outras através do número de pólos pares ρ.

 (2.04)

Para obter informações mais detalhadas sobre o motor de indução CA alimentado por inversor, consulte [2].

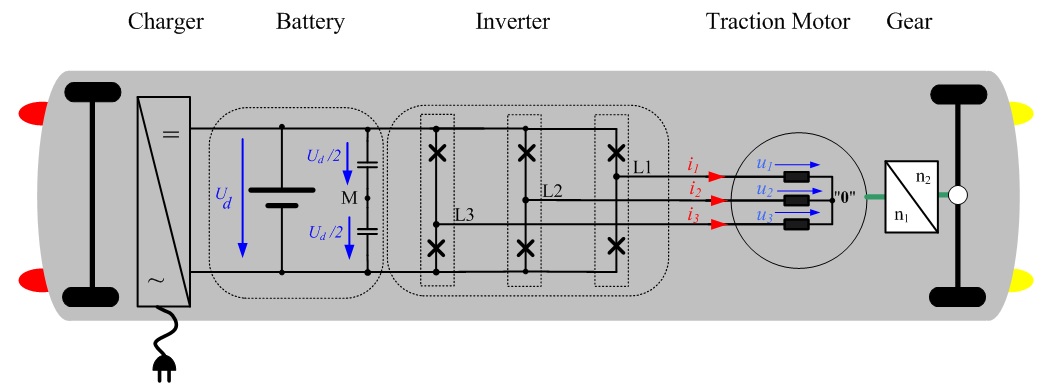
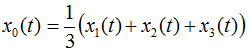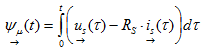Fig. 2.3: Diagrama simplificado do circuito equivalente de um motor de indução CA alimentado por inversor.

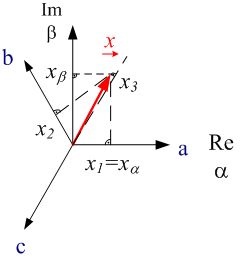
A fig. 3.1 mostra o comportamento temporal de um motor de indução CA alimentado por inversor de tensões de fase (u1 (t), U2 (t), U3 (t)) e correntes de fase (i1 (t), i2 (t), i3 (t)). As direções das correntes e tensões de contagem são mostrados na visão geral da figura 1.1. As grandezas vetoriais espaciais podem ser calculadas a partir das grandezas de fase medidas através da equação 2.02. Devido ao fato de que no Perception todas as variáveis precisam ser números reais, as partes reais e imaginárias do vetor espacial são calculados separadamente. A equação a seguir mostra este cálculo para a tensão de fase e a corrente de fase.

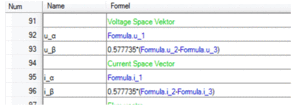
(3.01)

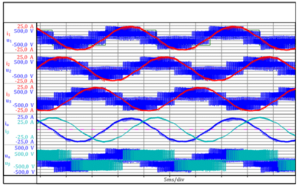
Fig. 3.1: Grandezas de fases medidas (i₁,i₂,i₃,u₁,u₂,u₃) e grandezas vetoriais espaciais calculadas (i_a,i_b,u_a,u_b) (Para usuários do Perception, essas medidas estão disponíveis no seguinte arquivo: Space Vector and Air GapTorque. pNRF. Este arquivo está disponível para download no site da HBM).

Cálculo do fluxo do estator de um motor de indução CA alimentados por inversor

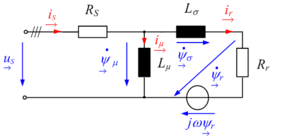
O vetor espacial do fluxo do estator  descreve o campo magnético em um motor de indução CA alimentado por inversor. O vetor espacial do fluxo do estator é obtido por integração da diferença entre a corrente do estator e a queda de tensão na resistência R_s do estator do motor.

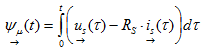
(3.06)

A baixa resistência do estator pode ser negligenciada frequentemente com alguns motores, dependendo dos requisitos de precisão. Como resultado da integração, o fluxo do estator é uma grandeza contínua. Embora, como se mostra na fig. 3.1, a tensão do estator mostra largura de banda modulada com comportamento pulsante, o real vetor espacial do fluxo do estator ψ_α(t) e as partes imaginárias ψ_β(t) são aproximadamente senoidais (fig. 3.2a). Como uma aproximação grosseira, a trajetória do vetor espacial do fluxo do estator segue uma trajetória circular. O raio da trajetória circular corresponde à amplitude do fluxo do estator.

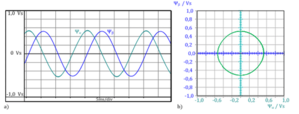
Fig. 3.2:  Vetor espacial do fluxo do estator do motor de indução CA alimentado por inversor
a) Comportamento temporal da parte real e imaginária
b) Trajetória do vetor espacial no plano complexo

Cálculo do Torque no Entreferro de um Motor de Indução CA Alimentado por Inversor

Com os motores de indução de corrente alternada alimentado por inversor, o chamado torque no entreferro ou interno pode ser calculado a partir da tensão ou fluxo e medições de correntes. O torque no entreferro consiste no torque de atrito interno inevitável do motor e o torque no eixo. Ignorando o torque de atrito, o torque interno calculado corresponde ao torque de aperto mecânico que pode ser medido com grande precisão utilizando um transdutor de torque [3].

A precisão do torque calculado depende do modelo de cálculo utilizado e a precisão de seus parâmetros do motor. O cálculo do torque interno pode ser usado como informação redundante complementando o sinal de medição de um transdutor de torque, porque o seu valor deve ser, pelo menos, da mesma ordem de grandeza que o momento mecânico. Além disso, o torque proporcional de um motor eléctrico pode ser correlacionado com todo o torque medido no sistema de transmissão utilizando um transdutor de torque. Uma aplicação potencial é, por exemplo, em um veículo híbrido, porque o seu motor de combustão e o motor elétrico atuam na mesma transmissão. Com o torque calculado do motor eléctrico, o torque do motor de combustão pode ser determinado.

É conhecido a partir da literatura [2] que o torque interno do motor de indução CA alimentado por inversor pode ser calculado a partir das correntes do estator e os fluxos magnéticos do estator.

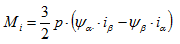
(3.06)

Aqui, ρ representa o número de par de pólos do motor de indução CA alimentados por inversor. Correntes e fluxos estão representados pelos componentes vetoriais espaciais. A fig. 3.3 mostra o comportamento temporal das correntes do estator e dos fluxos, assim como o momento internoM_i  calculado a partir destes valores. A ondulação de torque resultante é claramente visível. Alta freqüência de ondulação de torque é gerada como resultado da operação de comutação do inversor. É essencial identificar corretamente o período da corrente do motor para permitir que o torque no entreferro possa ser calculado no Perception.

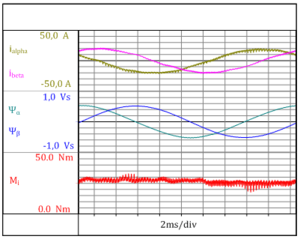
Fig. 3.3: Comportamento temporal da corrente do estator (i_α, i_β), fluxo do estator (ψ_α, ψ_β) e o torque no entreferro calculado M_i

Este artigo apresenta as medições em um motor de indução CA alimentados por inversor. Os valores de fase medidos são convertidos na chamada grandeza vetorial espacial para facilitar a análise dos resultados das medições. O fluxo magnético no motor de indução CA alimentados por inversor é calculado através da integração da tensão do estator. Estas grandezas medidas eletricamente combinadas com as grandezas magnéticas calculadas permitem que o momento do motor de indução CA alimentado por inversor possa ser calculado. Este cálculo de torque fornece um sinal de medição redundante complementando o sinal do transdutor de torque de alta precisão. O valor do torque calculado permite realizar uma verificação de plausibilidade da medida e identificar rapidamente os erros de medição.

Referências

[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft; Tagungsband 3. Tagung Innovation Messtechnik; 14. Mai 2013

[2] J. Teigelkötter: Energieeffiziente elektrische Antriebe, 1. Auflage, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3

[3] R. Schicker; G. Wegener: Drehmoment richtig messen; Hottinger Baldwin Messtechnik GmbH 2002, ISBN 3-00-008945-4  

[4] Berechnung von Leistungsgrößen mit Perception-Software
https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/

[5] www.hbm.com

Vetores Espaciais e Torque no Entreferro.pNRF