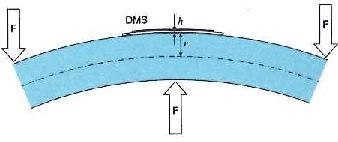
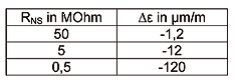
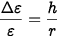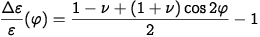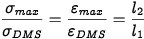Exatidão de medição em aplicações de análise experimental de tensão
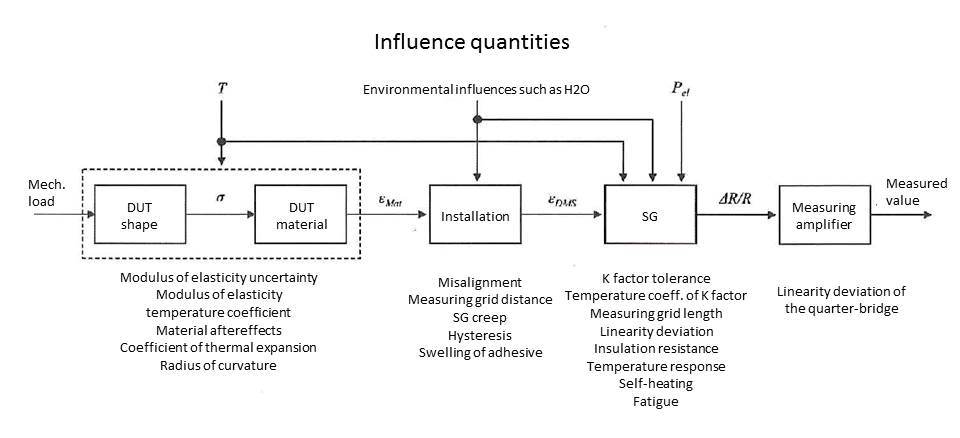
A tecnologia de strain gages com suas amplas possibilidades para compensação de erros foi otimizada ao longo das décadas. Mas ainda existem influências que podem afetar as medições feitas com esta tecnologia. O objetivo deste artigo é apontar estas fontes de erro (que, eventualmente, podem ser evitadas) quando os strain gages são usados na análise experimental de tensão e prestar assistência de forma que as incertezas de medição possam ser avaliadas já na fase de projeto.
Questões fundamentais na configuração de sua medição
As seguintes observações que podem lhe ser úteis antes de realizar medições com strain gauges em aplicações de análise experimental de tensões são um resumo das experências do autor. Os seguintes pontos são essenciais para as medições requeridas (ex.: proteção do ponto de medição) e a incerteza de medição que pode ser obtida:
- Quando o ponto de medição atingirá o fim de sua vida útil?
- Que magnitude terão os valores de deformação?
- Serão produzidas variações de temperatura? Em caso afirmativo, em que faixa e com qual velocidade?
- Existe algum fator ambiental especial (água, umidade, etc) que afete o ponto de medição?
- Sobre qual material será instalado o strain gauge (não homogêneo, anisotrópico, altamente higroscópico, etc)?
Um engenheiro de teste experiente estará procurando tais respostas já ao analisar a tarefa de medição (muito antes do primeiro strain gauge ser instalado). A resposta para a última pergunta decide se a medição será
- zero-point related ou
- non zero-point related