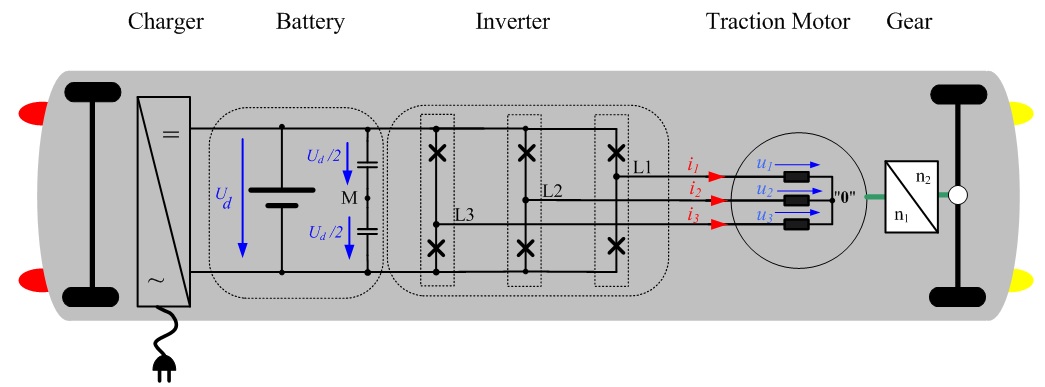
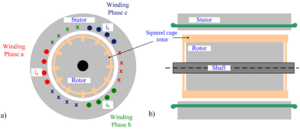
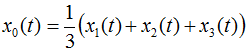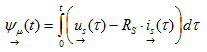Measurements on an Inverter-Fed AC Induction Motor
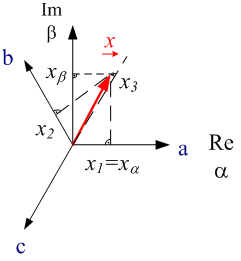
Fig. 3.1 shows the time behavior of an inverter-fed AC induction motor's phase voltages (u1(t),u2(t),u3(t)) and phase currents (i1(t),i2(t),i3(t)). The currents and voltages' counting direction is shown in the overview in figure 1.1. The space vector quantities can be calculated from the measured phase quantities using equation 2.02. Due to the fact that in Perception all variables need to be real numbers, the space vector's real and imaginary parts are calculated separately. The following equation shows this calculation for the phase voltage and the phase current.
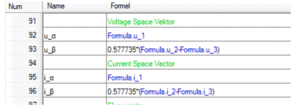
(3.01)
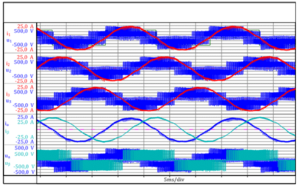
Fig. 3.1: Measured phase quantities (i1,i2,i3,u1,u2,u3) and calculated space vector quantities (ia,ib,ua,ub) (For Perception users, these measurements are available in the following file: Space Vector and Air GapTorque .pNRF. This file is available for download from the HBM website).
Calculating the stator flux of an inverter-fed AC induction motor
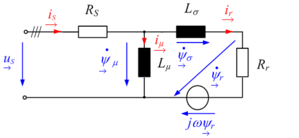
The stator flux space vector  describes the magnetic field in an inverter-fed AC induction motor. The stator flux space vector is obtained by integrating the difference between stator voltage and voltage drop at the motor's stator resistance Rs.
describes the magnetic field in an inverter-fed AC induction motor. The stator flux space vector is obtained by integrating the difference between stator voltage and voltage drop at the motor's stator resistance Rs.
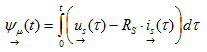
(3.06)
The often low stator resistance can be neglected with some motors, depending on the accuracy requirements. As a result of the integration, the stator flux is a continuous quantity. Even though, as shown in Fig. 3.1, the stator voltage shows pulse width modulated behavior, the stator flux space vector's real ψα(t) and imaginary parts ψβ(t) are approximately sinusoidal (Fig. 3.2a). As a rough approximation, the stator flux space vector's trajectory follows a circular path. The radius of the circular path corresponds to the amplitude of the stator flux.
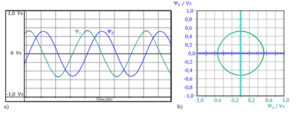
Fig. 3.2: Stator flux space vector of the inverter-fed AC induction motor
a) Time behavior of the real and imaginary parts
b) Trajectory of the space vector in the complex plane
Calculating the Internal Air-Gap Moment of an Inverter-Fed AC Induction Motor
With inverter-fed AC induction motors, the so-called internal or air-gap moment can be calculated from voltage or flux and current measurements. The internal air-gap moment consists of the motor's internal inevitable friction torques and the torque at the shaft. Ignoring frictional torque, the calculated internal torque corresponds to the mechanical torque which can be measured very precisely using a torque transducer [3].
The accuracy of the calculated torque depends on the calculation model used and the accuracy of its motor parameters. The calculation of the internal torque can be used as redundant information complementing a torque transducer's measurement signal, because its amount should at least be on the same order of magnitude as the mechanical moment. Moreover, the proportional torque of an electric motor can be correlated with the entire drive train's torque measured using the torque transducer. A potential application is, for example, a hybrid vehicle, because its combustion engine and electric motor act on the same drive train. With the calculated torque of the electric motor, the moment of the combustion engine can be determined.
It is known from the literature [2] that the internal torque of inverter-fed AC inductionmotors can be calculated from the stator currents and magnetic stator fluxes.
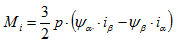
(3.06)
Here, ρ represents the inverter-fed AC induction motor's number of pole pairs. Currents and fluxes are represented by their space vector components. Fig. 3.3 shows the time behavior of the stator currents and the fluxes, as well as the internal air-gap moment Mi calculated from these values. The resulting torque ripple is clearly visible. High-frequency torque ripple is generated as a result of the inverter's switching operation. It is essential to correctly identify the period of the motor current's fundamental to enable the air-gap moment to be calculated in Perception.
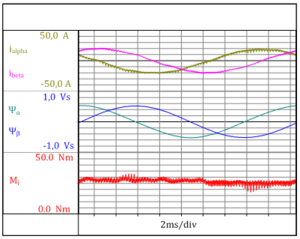
Fig. 3.3: Time behavior of stator current (iα, iβ), stator flux (ψα, ψβ) and the calculated air-gap moment Mi