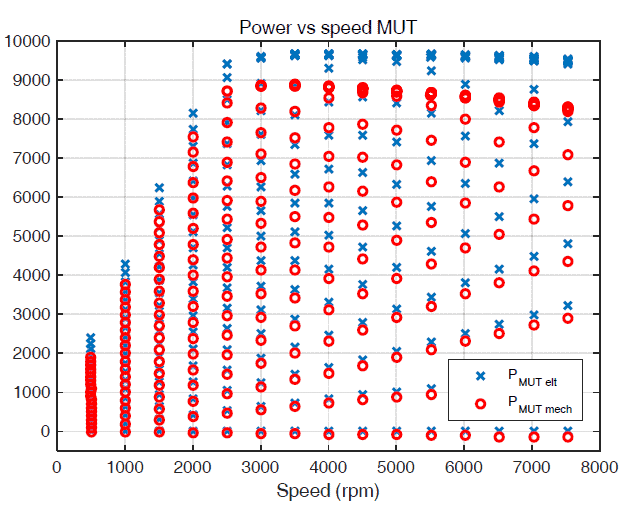
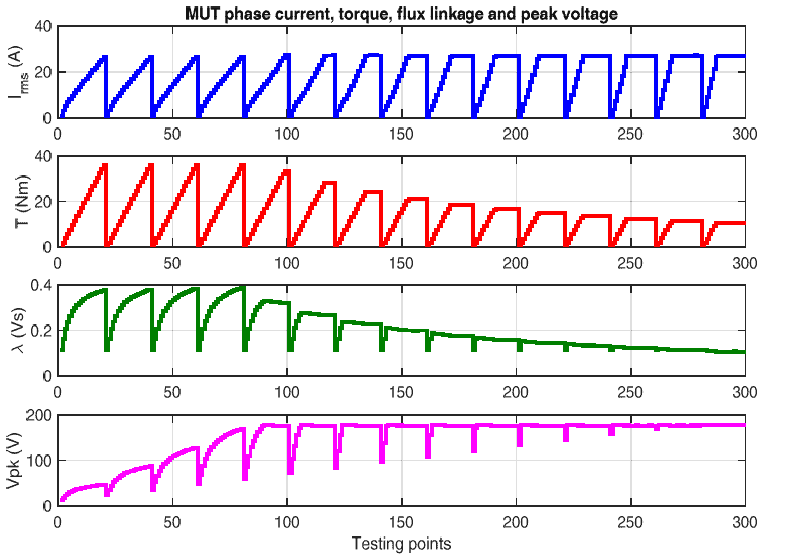
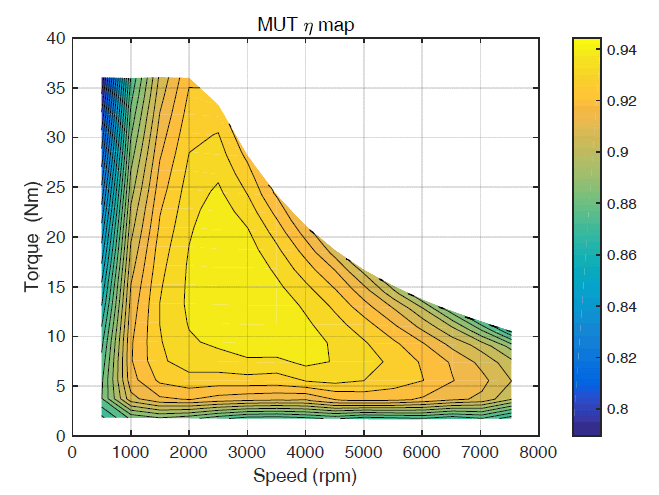
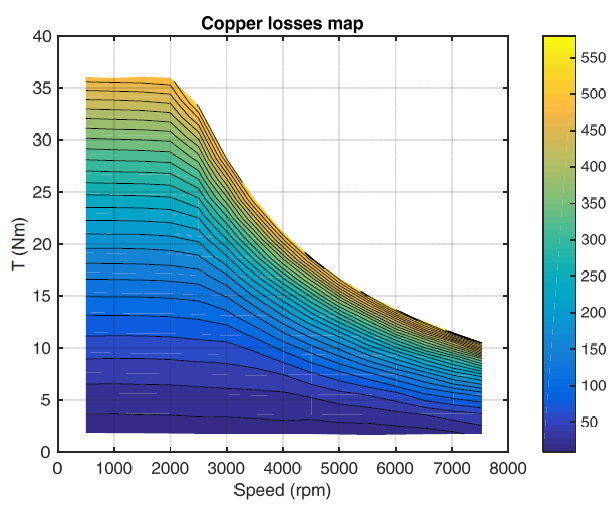
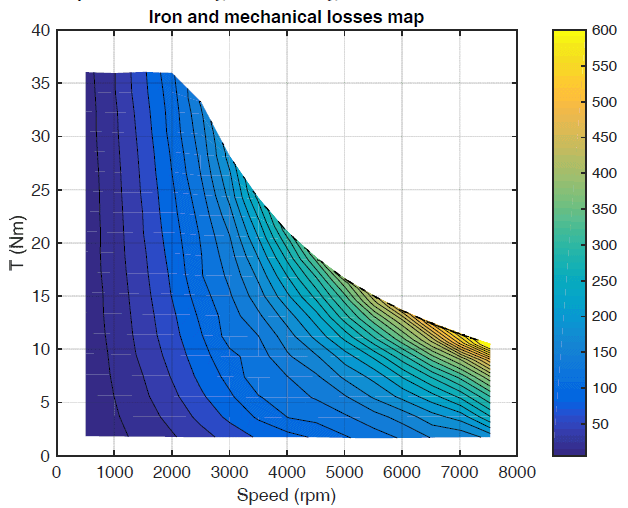
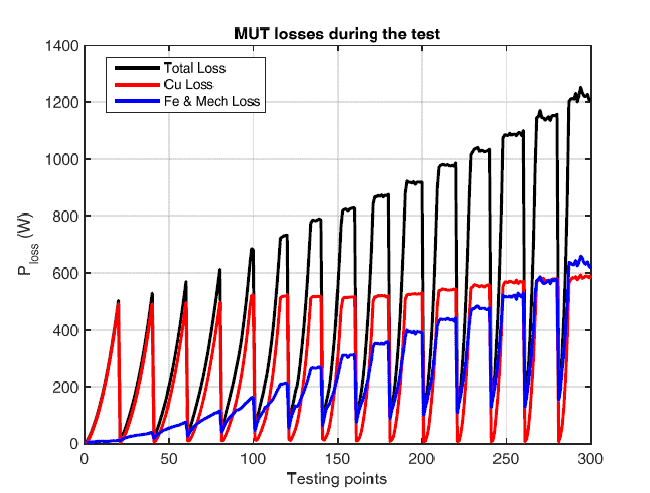
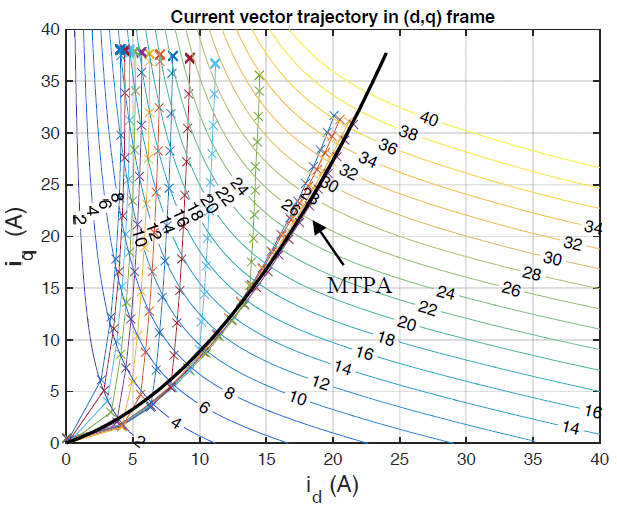
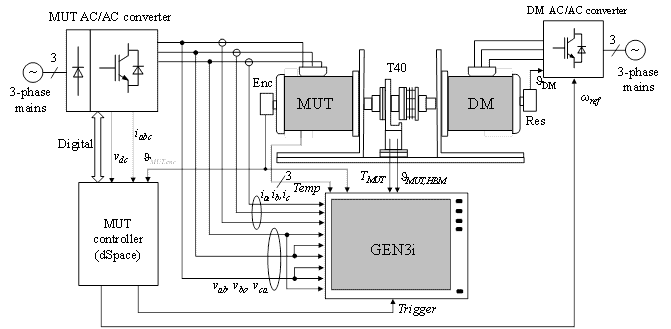
The test rig used for efficiency and loss mapping is shown in Fig.1. The test rig consists of the following main elements:
- Motor under Test (MUT) is an Internal Permanent Magnets (IPM) motor
- The motor controller is a dSpace board with a dedicated analog/digital interface
- The Driving Motor (DM) is a speed-controlled Permanent Magnet (PM) motor fed by a bi-directional converter whose speed reference is provided by the dSpace board using an analog dSpace DAC (digital-to-analog converter) output. Another solution is to use a CAN or RS422 interface, depending also of the communication capability of the converter that supplies the DM











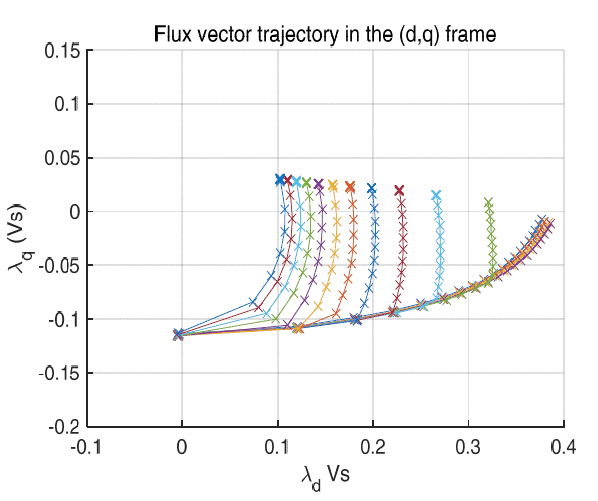
 is the average stator temperature computed as the mean value of the k measured stator temperatures.
is the average stator temperature computed as the mean value of the k measured stator temperatures.







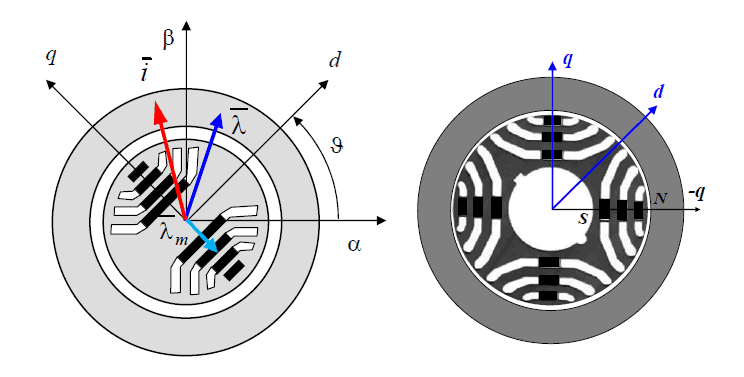
 is the electrical position that is calculated from the measured mechanical position, the pole-pairs number and an offset that must be known.
is the electrical position that is calculated from the measured mechanical position, the pole-pairs number and an offset that must be known.