Uso di tecniche statistiche per validare i dati delle prove in campo per l'analisi della fatica
Questo articolo descrive alcune tecniche statistiche per il rilevamento dei dati di misura e per la previsione di ciò che sarebbe la storia temporale ed i danni provocati dalla fatica, se i dati fossero stati rilevati per periodi molto più lunghi.
Sommario
Durante ogni prova sul campo lo sperimentatore si trova di fronte alla decisione se i dati raccolti sono sufficienti per caratterizzare una particolare operazione. Questo articolo descrive alcune tecniche statistiche per rilevare i dati di misuri e per prevedere ciò che sarebbe la storia temporale ed i danni provocati dalla fatica, se i dati fossero stati rilevati per periodi molto più lunghi. Si considerano sufficienti i dati rilevati quando convergono i danni da fatica calcolati sia dai dati misurati che dalle storie temporali previste.
Basi
Un fattore importante nella progettazione di veicoli o strutture è l'anticipazione della severità di utilizzo in esercizio. In un veicolo nuovo, l'utilizzo in esercizio è sconosciuto e vengono sovente condotte brevi prove per determinare i carichi agenti sulla struttura e le conseguenti sollecitazioni. La storia di caricamento di un veicolo contiene frequentemente sia una parte deterministica che una parte casuale. Ad esempio, un autocarro può avere un ciclo di servizio deterministico dovuto al carico e scarico combinati con una serie di carichi casuali dovuti alla guida su differenti superfici. I carichi dei cicli di servizio si possono considerare sia come di natura variabile che di popolazione diversa rispetto ai carichi di guida. Un problema che tutti gli sperimentatori incontrano è quello di determinare quando si sono acquisiti dati sufficienti per caratterizzare una particolare condizione di utilizzo del servizio.
La Figura 1 mostra la storia di carico misurata in campo delle sollecitazioni delle sospensioni anteriori in un veicolo per tutti i terreni (all terrain vehicle ( ATV )), lungo una pista di prova. la storia è stata registrata per dieci giri.

Figura 1: Dieci giri della pista di prova
Nonostante si tratti di una pista di prova attentamente controllata e di un unico autista, si nota facilmente nella figura la variabilità del carico durante ciascun giro.
Dal punto di vista dei danni da fatica, i dati in Fig. 1 sono sufficienti per caratterizzare l'utilizzo di servizio per la vita prevista del componente? A questa domanda si può rispondere usando la variabilità nella storia del carico misurato, per proiettare quale sarebbe stato il danno da fatica previsto e la storia del carico se le sollecitazioni fossero state misurate per un periodo più lungo.
L'analisi della variabilità nel dominio del tempo per funzioni di carico sul tempo non è fattibile e non è necessaria. Nella fatica, l'istogramma rainflow dei carichi è più interessante che la soria del carico in se stessa, dato che il danno da fatica viene calcolato da esso.
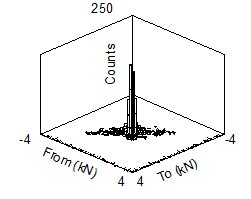
Figura 2: Istogramma Rainflow
Due istogrammi rainflow dimensionali contengono informazioni sia sui campi di carico che sulle medie. La Figura 2 mostra l'istogramma rainflow dei dati provenienti dalla Fig. 1, in un formato To-From (A-Da). Questo tipo di istogramma preserva gli effetti delle sollecitazioni medie che sono solitamente importanti per l'analisi della fatica.
I dati provenienti dalla Fig. 2 sono tracciati come diagramma di eccedenza cumulativa in Fig. 3.
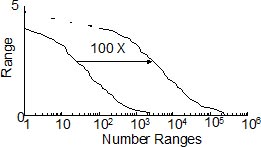
Figura 3: Diagramma di eccedenza
Nel lato sinistro del diagramma viene mostrata la curva di eccedenza per la storia di carico originale. Se i dati di prova fossero stati misurati per 1000 giri (100 volte più a lungo), si aspettarebbe una distribuzione traslata verso destra ed avente la medesima forma. La linea tratteggiata mostra schematicamente che si aspettano carichi più elevati per periodi più lunghi. Sebbene il diagramma di eccedenza sia più facile da visualizzare, esso trascura preziose informazioni sugli effetti medi.
In questo articolo mostriamo come la variabilità in un istogramma rainflow misurato possa essere usato per stimare l'istogramma rainflow atteso per periodi più lunghi. Tale istogramma estrapolato può poi essere impiegato per ricostruire una nuova storia temporale più lunga, per le prove od analisi.
Estrapolazione Rainflow
L'estrapolazione degli istogrammi rainflow fu proposta per primo da Dressler [1]. Qui viene data una breve descrizione del concetto. Per i dettagli i lettori possono fare riferimento ad [1]. L'istogramma rainflow viene trattato come una distribuzione bidimensionale di probabilità. Si può ottenere una semplice densità di distribuzione dividendo il numero di cicli in ogni recipiente (bin) dell'istogramma per il numero totale dei cicli. Si può costruire un nuovo istogramma corrispondente a qualsiasi numero dei cicli totali, disponendo casualmente i cicli nell'istogramma in base alla loro probabilità di occorrenza. Tuttavia, questo approccio sarà essenzialmente lo stesso che moltiplicare i cicli dell'istogramma per un fattore di estrapolazione. Ma ciò non è realistico. Anche lo stesso autista sulla stessa pista di prova non può ripetere la storia del carico. Ad esempio, ogni volta che l'autista centra una buca i carichi saranno un pò differenti. Ciò viene chiaramente mostrato nei dieci giri di Fig. 1. Il picco di carico dovuto ad un particolare evento verrà inserito in un recipiente individuale dell'istogramma rainflow. Durante il giro successivo, questo carico avrà un valore massimo diverso e sarà inserito in un recipiente nello stesso dintorno del primo giro.
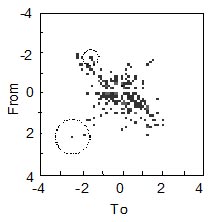
Figura 4: Variabilità istogramma
La Figura 4 mostra un istogramma rainflow con una vista bidimensionale. Considerare che l'evento proceda da 2 a –2,5. La volta successiva che si ripete, esso sarà da qualche parte nelle vicinanze di ( 2, -2,5 ), indicato dal grande cerchio tratteggiato. Non ci sono molti dati in quesa zona dell'istogramma e ci si attende una notevole variabilità. Consideriamo ora i cicli da –2 a –1,5. Qui ci sono molti più dati e ci si aspetta che la variabilità sia molto inferiore, come indicato dal piccolo cerchio tratteggiato. L'istogramma di estrapolazione rainflow ha essenzialmente il compito di trovare la funzione di distribuzione bidimensionale della probabilità partendo dai dati rainflow originali.
Per una data serie X di valori presi da una popolazione continua, ci sono molti modi per costruire una distribuzione di probabilità dei dati. Esistono due classi generali di stima della densità di probabilità: parametrica e non parametrica. Nella stima della densità parametrica, si presume che la data serie di valori si adatti ad una predeterminata distribuzione teorica della probabilità. I parametri di forma per la distribuzione devono essere stimati dai dati. Gli estimatori della densità non parametrica non fanno ipotesi circa la distribuzione dell'intera serie di dati. Un istogramma è l'estimatore non parametrico della densità. Ai fini dell'estrapolazione, si desidera convertire i punti discreti di un istogrammain una densità continua di probabilità. Gli estimatori di Kernal [2-3] forniscono un modo comodo per stimare la densità di probabilità. Il metodo può essere pensato come l'adattamento della distribuzione presunta di probabilità in una zona locale dell'istogramma. La dimensione della zona locale è determinata dalla larghezza di banda dell'estimatore. Ciò è indicato dalla dimensione del cerchio in Fig. 4. La larghezza di banda adattativa per il kernal è determinata dalla quantità di dati che si trovano nella vicinanza del punto preso in considerazione.
I metodi statistici sono ben sviluppati per le zone dell'istogramma in cui c'è una moltitudine di dati. Si richiedono considerazioni particolari per le zone scarsamente popolate [4]. Il massimo campo di carico previsto per l'istogramma estrapolato viene stimato dall'adattamento Weibull alle grandi ampiezze dei campi di carico. Tale stima viene quindi utilizzata per determinare una larghezza di banda adattiva per le zone di dati sparsi dell'istogramma. Dopo aver determinato la larghezza di banda adattiva, si può calcolare la densità di probabilità dell'intero istogramma. L'istogramma previsto per ogni numero totale di cicli desiderato, viene costruito inserendo casualmente i cicli nell'istogramma con l'appropriata probabilità. Si deve notare che questo processo non produce un'unica estrapolazione. Si possono effettuare molte estrapolazioni con il medesimo fattore di estrapolazione, in modo che si possano ottenere alcune informazioni sulla variabilità della risultante storia del carico.
In Fig. 5 sono riportati i risultati dell'estrapolazione di 1000 volte la storia del carico. È più facile visualizzare i risultati dell'estrapolazione quando essi vengono mostrati in termini di diagramma di eccedenza come in Fig. 6. Nella figura ci sono due tracciati: uno proveniente dai dati di Fig. 5 e l'altro raffigurante le 1000 ripetizioni della storia di carico originale.
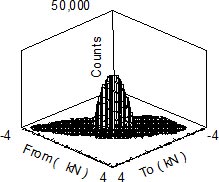
Figura 5: Istogramma estrapolato
La Tabella 1 riporta i risultati delle vite alla fatica calcolate dalle varie estrapolazioni della storia di carico originale. Le vite a fatica rappresentano la vita operativa presunta della struttura, espressa in ore. Nei calcoli è stato impiegato un semplice approccio SN. Si può utilizzare qualsiasi conveniente analisi della fatica e combinarla con una descrizione probabilistica delle proprietà del materiale.
Tabella 1: Vite alla fatica
Storia | Vita | Massimo | Minimo |
|---|---|---|---|
Originale | 29.890 | 1,89 | -2.12 |
10X | 26.760 | 2,25 | -2,50 |
100X | 16.170 | 2,88 | -3,25 |
1000X | 10.190 | 3,25 | -3,63 |
Come previsto, le vite alla fatica calcolate sono più basse per storie di carico più lunghe, a causa dei carichi più elevati negli istogrammi estrapolati. Tuttavia, i carichi più alti rappresentano una previsione più realistica dei carichi operativi durante l'intero ciclo di vita della struttura.
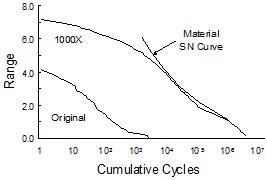
Figura 6: Distribuzione dei cicli e dei danni da fatica
Un metodo efficace per visualizzare i cicli dannosi consiste nel tracciare i cicli di distribuzione ed il comportamento del materiale sulla stessa scala, come mostrato in Fig. 6. Le proprietà del materiale sono scalate in modo che esse abiano le stesse unità della storia del carico, e questo grafico raffiguri la vita a fatica prevista sotto ampiezza di carico costante. Il punto di tangenza delle due curve fornisce un'indicazione del campo di cicli più dannoso. In questa storia, il massimo campo di cicli di carico non è il più dannoso, infatti i cicli di carico più dannosi per questa storia di carico sono a circa ½ del massimo campo di carico nell'istogramma estrapolato.
Ricostruzione Rainflow
L'obiettivo della ricostruzione rainflow è quello di ottenere una storia temporale che abbia danni a fatica similari all'istogramma rainflow originale [5]. In sostanza, si desidera effettuare un conteggio rainflow all'indietro. Partendo dall'istogramma rainflow, si ricostruisce una storia temporale, ciclo per ciclo, che abbia il medesimo conteggio rainflow. Il più grande ciclo complessivo nell'istogramma è noto. Nel formato To-From (A-Da), il conteggio rainflow distingue la differenza fra un ciclo Peak-Valley-Peak (PV) (picco-valle-picco) ed un ciclo Valley-Peak-Valley (VP) (valle-picco-valle). I cicli VP sono memorizzati sopra la diagonale di principio dell'istogramma ed i cicli PV sono memorizzati sotto di essa. Per ogni ciclo VP, la riga dell'istogramma è inferiore alla colonna. Similmente, per ogni ciclo PV la colonna è inferiore alla riga. Il processo per l'inserzione dei cicli VP è illustrato in Fig. 7. I numeri a sinistra indicano i recipienti dell'istogramma, riga e colonna, e sono proporzionali alla magnitudo della storia di carico risultante. La storia di carico ricostruita è contrassegnata P e V ed il ciclo da inserire è contrassegnato con r et c.
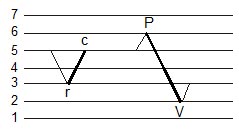
Figura 7: Inserimento di un ciclo VP
Un ciclo VP ( r < c ) può essere inserito in qualsiasi inversione PV se c <= P ed r > V. Un ciclo VP non può essere inserito in un ciclo PV della stessa magnitudo.
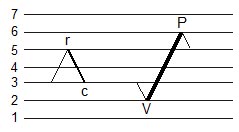
Figura 8: Inserimento di un ciclo PV
La Figura 8 mostra l'inserimento di un ciclo PV. Un ciclo PV ( c < r ) può essere inserito in qualsiasi inversione VP se r < P et c >= V. Un ciclo PV non può essere inserito in un ciclo VP avente la stessa magnitudo.
Queste due semplici regole sono la base per la ricostruzione rainflow. Il processo inizia con il ciclo più grande, sia esso PVP che VPV. Il successivo ciclo più grande viene poi inserito nell'appropriata posizione della storia temporale ricostruita. Dopo i primi pochi cicli, esistono molte possibili posizioni in cui inserire i cicli minori. Tutte le possibili posizioni d'inserzione sono determinate e si selezionano casualmente.
Riassunto
L'affidabilità di un veicolo o di una struttura è influenzata dalla distribuzione del carico durante l'intero utilizzo operativo. Viene descritta una tecnica per stimare la durevolezza a lungo termine partendo dai carichi misurati per un breve periodo.
Bibliografia
[1] Dressler, K, B. Grunder, M. Hack and V.B. Koettgen, "Extrapolation of rainflow matrices", SAE Paper 960569, 1996
[2] Silverman, B.W. "Density estimation for statistics and data analysis" Chapman and Hall, New York, 1986
[3] Scott, D.W. "Multivariate density estimation" Wiley, New York, 1992
[4] Roth, J.S. "Statistical modeling of rainflow histograms" Materials Engineering-Mechanical Behavior Report No. 182, UILU-ENG 98-4017, University of Illinois, 1998
[5] Khosrovaneh, A.K. and N.E. Dowling, "Fatigue loading history reconstruction based on the rainflow technique", International Journal of Fatigue, Vol. 12, No. 2, 1990, 99-106