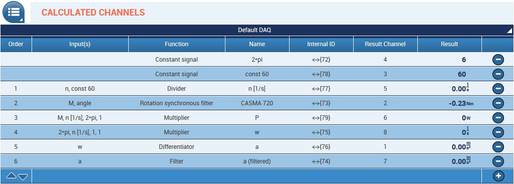
Create a calculated channel
Create a new calculated channel “rotation synchronous filter” in the Analysis category.
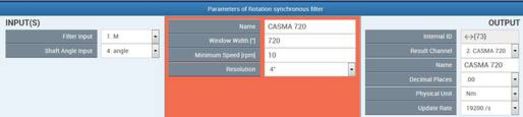
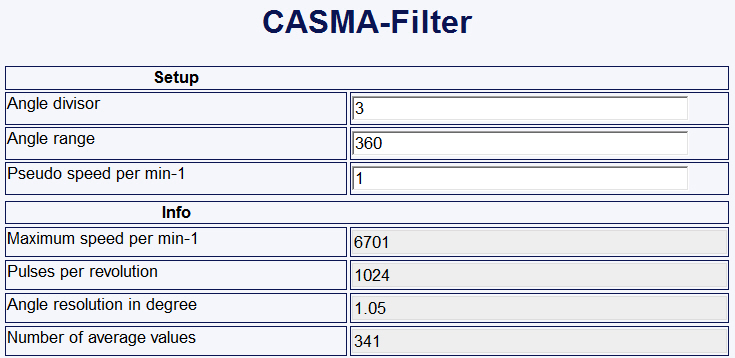
Adjust parameters
- Filter Input: Enter the signal to be filtered here.
- Shaft Angle Input: Enter the signal of the angle of rotation sensor here. The measured values must be between 0° and 360°.
- Window Width: Specify the range for taking the moving average. The width must be between 30° and 720°. The default setting is 180°. The ratio of the window width to the resolution must be less than 180.
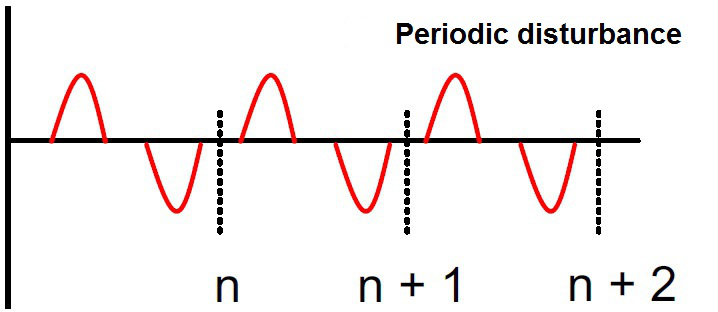
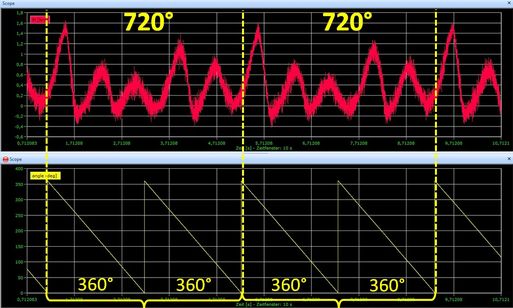
The window width can be easily determined experimentally by projecting the periodic time on the disturbance to the angle of rotation (see screenshot). In this example, there is a periodic disturbance every 720°.
- Minimum Speed: This virtual rotational speed is applied when the active rotational speed is less than the defined minimum rotational speed.
- Resolution: This value determines how often (how many degrees each time) a new average will be calculated. Note that the maximum permitted permissible rotational speed depends on this value because the speed of calculation is determined by the overall update rate.
The theoretical value is derived by: Maximum rotational speed = resolution * overall update rate / 6.
For practical purposes you should use values that amount to only 10 to 20% of this theoretically possible maximum rotational speed.
Resolution | The theoretical maximum rotational speed at an overall update rate of 19,200 Hz | The theoretical maximum rotational speed at an overall update rate of 38,400 Hz |
1° | 3200 rpm | 6400 rpm |
2° | 6400 rpm | 12,800 rpm |
4° | 12,800 rpm | 25,600 rpm |
6° | 19,200 rpm | 38,400 rpm |
8° | 25,600 rpm | 51,200 rpm |
The following multiples of the rotational speed are suppressed depending on the window width:
Window width | Multiples |
90° | 4, 8, 12, … |
120° | 3, 6, 9, … |
180° | 2, 4, 6, … |
360° | 1, 2, 3, … |
720° | 0, 5, 1, 1, 5, … |
Note: If one of the source signals is invalid, the output signal will be invalid as well.
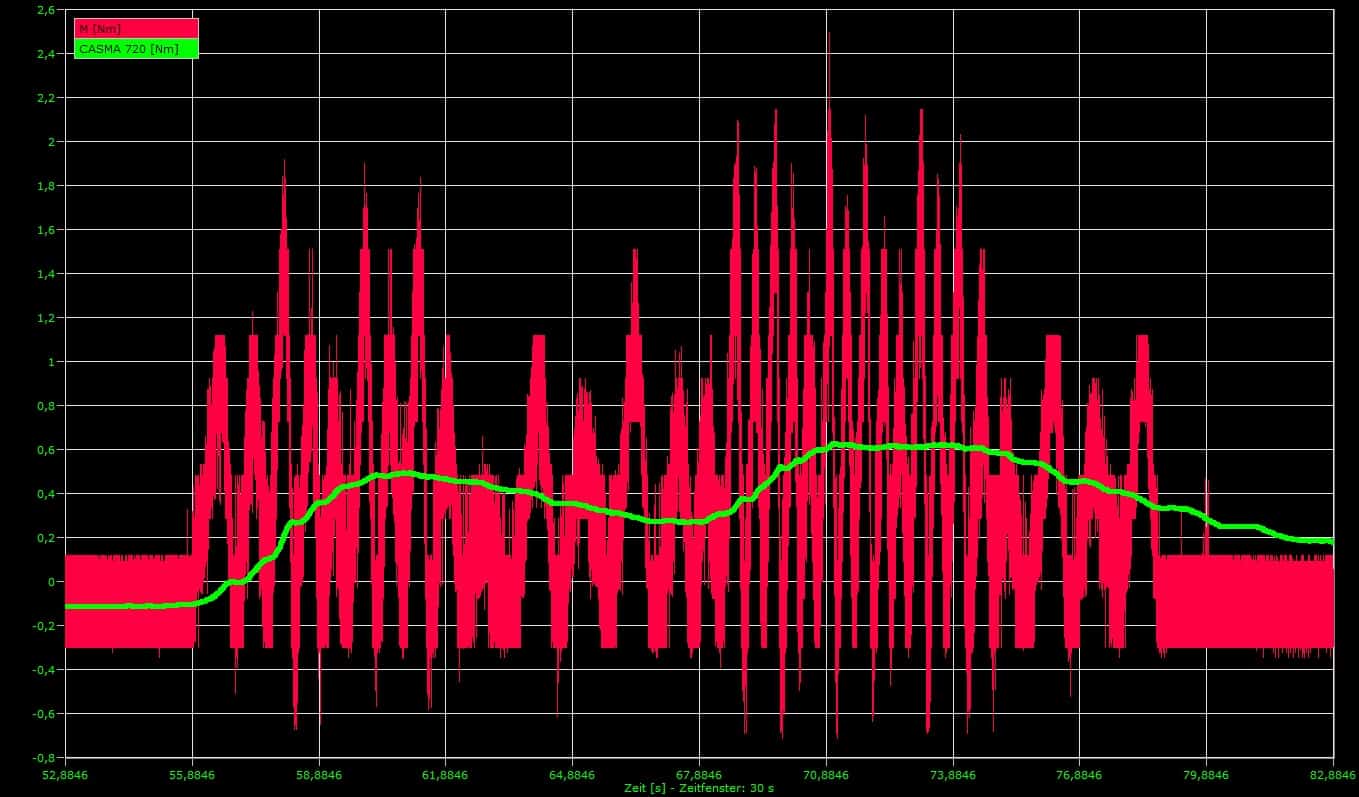
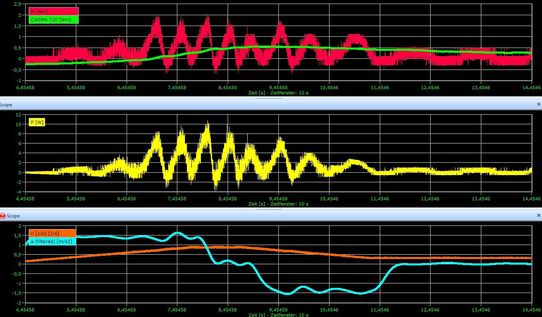
CASMA in action
You will see the unfiltered torque signal which is red, and the filter torque signal filtered using CASMA in green.
It can be seen clearly that the CASMA filter achieves excellent stabilization of torque measurements in correlation to the engine speed, which also changes over time. The greater the width of this filter, the better the results.