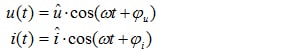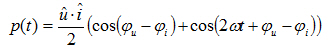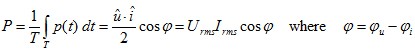Introdução
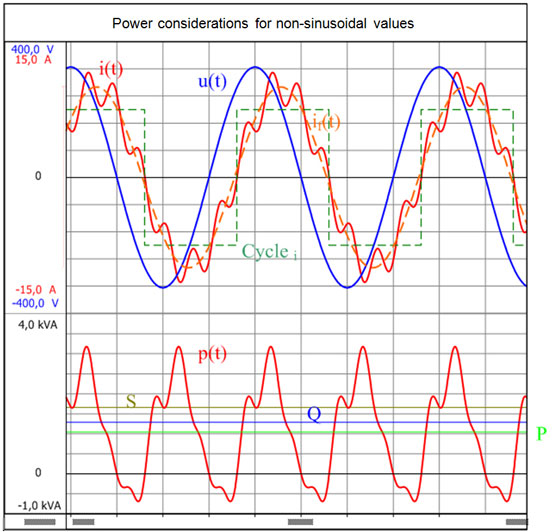
As máquinas elétricas convertem energia elétrica e energia mecânica. A direção do fluxo de energia é identificada pelo modo no qual a máquina elétrica está funcionando. No modo de motor, a energia elétrica é convertida em energia mecânica. No modo de gerador, a máquina elétrica é acionada e converte energia mecânica em energia elétrica. Os conversores de energia são identificados pela energia convertida por unidade de tempo ao invés de simplesmente fazê-lo pela energia que é convertida. Este valor é chamado de potência instantânea ou p(t).
![]()
(1.01)
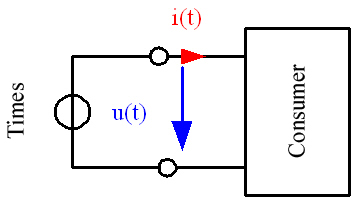
A Fig. 1.1 mostra uma rede de dois fios com uma fonte de energia e o consumidor correspondente. A tensão aplicada u(t) e a corrente do consumidor i(t) podem ser medidas nos pontos de medição. A potência instantânea é derivada do produto dessas variáveis:
![]()
(1.02)
O sistema de setas utilizado na Fig. 1.1 mostra como o consumidor absorve a energia quando a energia instantânea é positiva (p(t) >0). Se a energia instantânea for negativa (p(t) <0), o consumidor gera potência para a fonte.
</font>
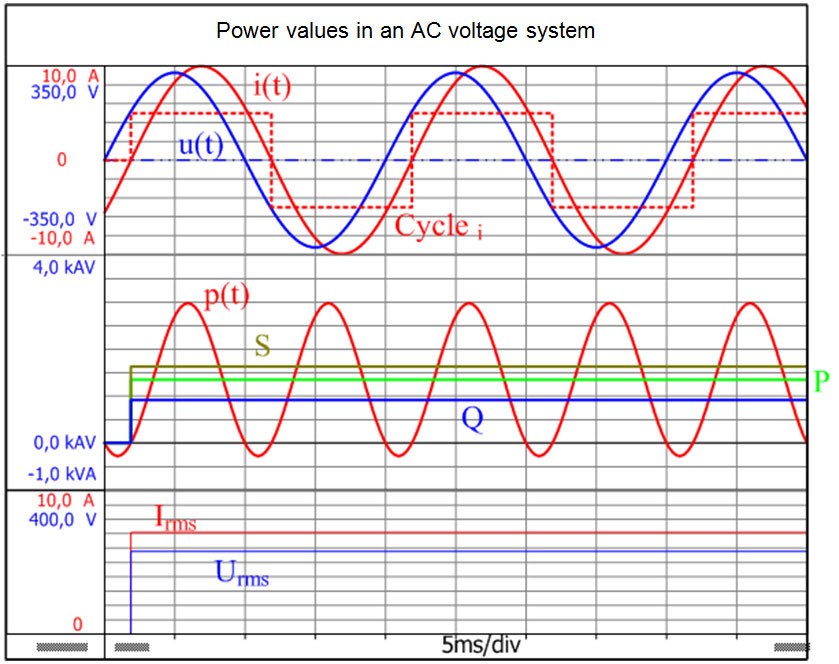
O valor médio da potência instantânea p(t) sobre a duração do ciclo T é chamada, em engenharia elétrica, de potência efetiva P.
![]()
(1.03)
O processo para determinar a potência ativa, reativa e aparente das curvas de corrente e tensão medidas com o Perception são descritas abaixo.
A implementação da fórmula (1.03) no software Perception é mostrada pelo exemplo extraído abaixo da base de dados de fórmulas do Perception (1.04).

(1.04)