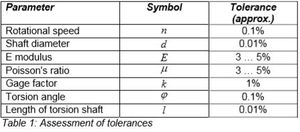
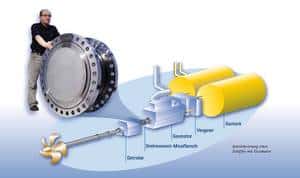
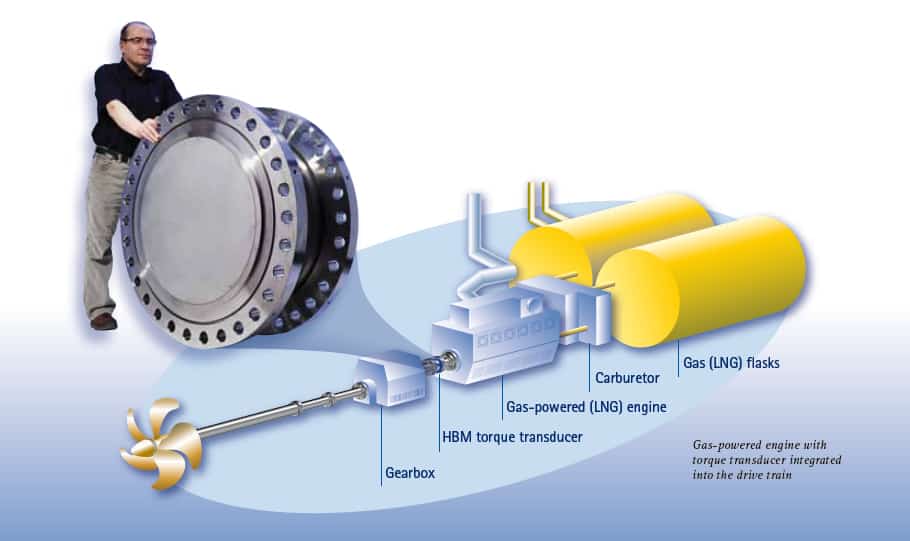
Power Measurement on Large Drives with Combustion Engines
1. Providing a power signal
Modern drive concepts with large combustion engines require precise and fast response of the engine's control systems (e.g. for fuel supply) to respond to abruuptly varying loads. Here, it is essential to ensure that sufficient power is supplied at any time and that, at the same time, the engine features low fuel consumption and safe operating parameters. This requires that a power signal is provided which - with vehicles, compressor and pump systems - needs to be generated using special measuring devices. In general, there are three different approaches:
- The power signal is provided indirectly by measuring specific auxiliary quantities such as flow rate, temperature, and pressure and then computing the power. With this approach, the power signal's uncertainty of measurement is very high. An additional drawback is that the values of the auxiliary quantities are not synchronous to the processes determining the engine power.
- The power signal is provided indirectly by measuring specific auxiliary quantities on the input shaft. This includes all methods involving measurement either of the strain resulting from shaft torsion on its surface or of the shaft's torsion angle. In both cases, the power is computed following the measurement of the auxiliary quantities.
- The power signal is provided directly by measuring torque in the input shaft.
The following article compares direct power measurement with indirect power measurement on and in the drive train respectively (approaches b. and c.) with regard to the uncertainties of measurement that can be achieved.
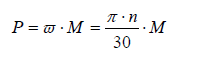 (1)
(1)
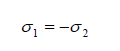 (3)
(3)
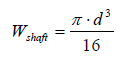 (5)
(5)
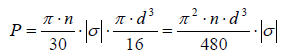 (6)
(6)
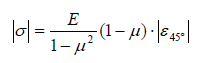 (7)
(7)
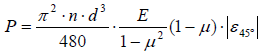 (8)
(8)
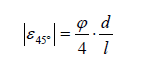 (9)
(9)
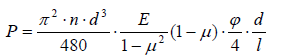 (10)
(10)