도입
전기 기기는 전기 에너지와 역학 에너지를 상호 전환시킵니다. 에너지 흐름의 방향은 전기 기기 운용상의 모드 지정으로 식별됩니다. 전동기 모드에서는 전기 에너지를 역학 에너지로 전환시키고, 발전기 모드에서는 구동된 전기 기기를 통해 역학적 에너지가 전기 에너지로 전환됩니다. 에너지 변환기는 단순히 에너지 전환만 식별하는 것이 아니고 단위 시간당 전환된 에너지를 식별합니다. 이 값을 순시 전력 또는 p(t)라 합니다.
| (1.01) |
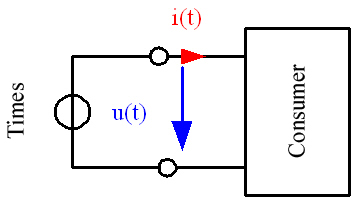
그림1.1은 하나의 에너지 소스를 가진 2선식 망과 해당 소비기에 대한 것입니다. 인가 전압 u(t) 과 소비기 전류i(t) 는 계측점에서 계측 가능합니다. 순시 전력은 이런 변수의 곱에서 얻어집니다.
| (1.02) |
그림 1.1의 소비기 수치 화살표 장치는 순시 전력이 양일 때(p(t) >0) 그 소비기로의 전력 인가 방법을 보여 줍니다. 순시 전력이 음이면(p(t) <0), 소비기는 전력을 소스에 공급합니다.
주기 T 의 기간 동안에 순시 전력 p(t)의 평균값은 전기 공학에서 유효 전력 P입니다
| (1.03) |
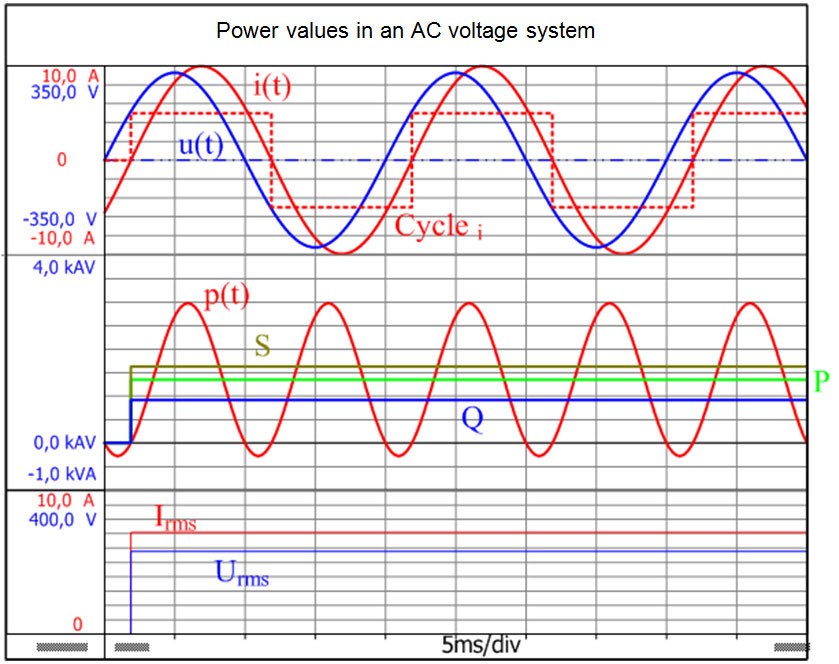
Perception으로 계측한 전류와 전압 곡선에서 유효, 무효 및 피상 전력을 결정하는 과정이 아래에 설명되어 있습니다.
아래의 예는 Perception 공식 데이터베이스(1.04)에서 발췌한 Perception 소프트웨어의 실행 공식(1.03)입니다.
 | (1.04) |

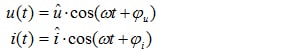
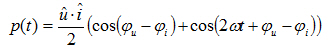 (2.02)
(2.02)
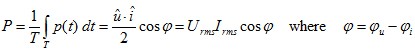 (2.03)
(2.03)
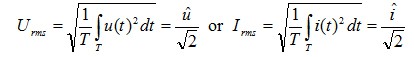
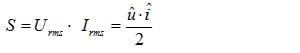 (2.05)
(2.05)
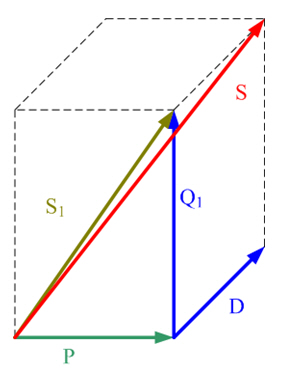
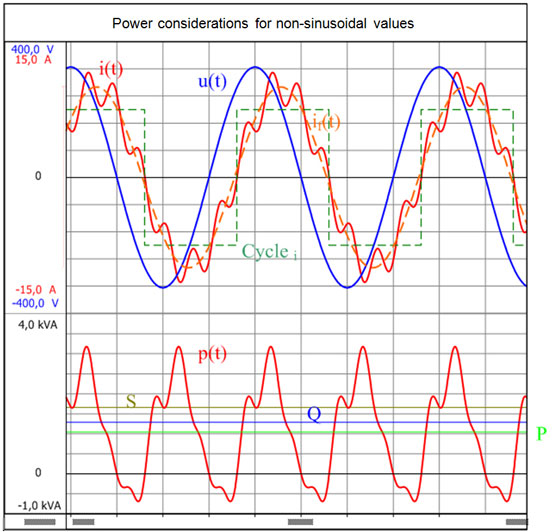
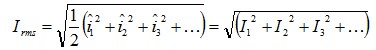
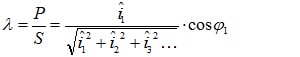
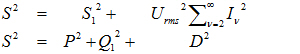
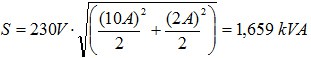
 에 대한 전력량만을 먼저 제시했습니다. 그리고 사인파 전압과 비사인파 전류 곡선을 나타내는 부하의 경우에 대한 전력값을 하나의 샘플 계산을 써서 설명했습니다.
에 대한 전력량만을 먼저 제시했습니다. 그리고 사인파 전압과 비사인파 전류 곡선을 나타내는 부하의 경우에 대한 전력값을 하나의 샘플 계산을 써서 설명했습니다.