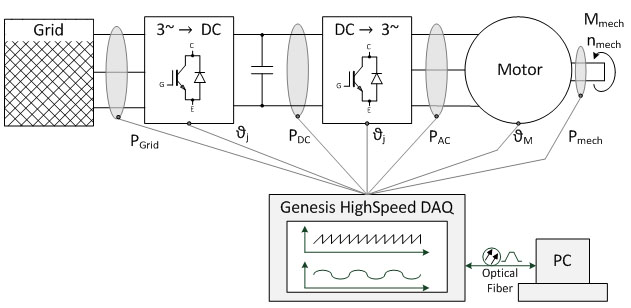
Várias grandezas físicas devem ser gravadas, salvas e condicionadas em sistemas de medição de energia, como mostrado na fig. 1.1, com uma unidade trifásica. Os Gravadores de dados Genesis HighSpeed permite a aquisição síncrona de todas as grandezas mais importantes em sistemas elétricos com um grande número de canais e alta taxa de amostragem [1]. Especialmente em sistemas que são fornecidos com uma corrente trifásica ou que gera um sistema trifasico, usando vetores espaciais para realizar a medição de grandezas, é mais fácil de se interpretar em um visor dedicado. Vetores espaciais também podem ser usados para representar estados de funcionamento estáticos assim como processos dinâmicos de balanceamento. Neste documento, as equações de definição para vetores espaciais e as regras de conversão para diferentes sistemas de coordenadas serão explicados inicialmente. Em seguida, será explicado como usar vetores espaciais para medir grandezas físicas de equipamentos síncronos permanentemente excitados (PSM - Permanently excited Synchronous Machines). Uma bancada com Perception foi preparada [3] para experimentar estes métodos de forma independente.
Cálculo e interpretação de grandezas medidas na tecnologia de energia elétrica, como vetores espaciais, com o software Perception da HBM
Resumo
Vetores espaciais são freqüentemente usados para uma interpretação clara e concisa de grandezas medidas em sistemas de conversão de energia elétrica, como trnsformadores ou motores de indução. Informações adicionais sobre o estado operacional destes conversores de energia podem ser determinadas se os vetores espaciais dependentes da função tempo são feitas como curvas de locus em um plano complexo. Para simplificar ainda mais a interpretação destas grandezas medidas, os vetores espaciais podem ser realizados em sistemas de coordenadas rotativas. Este artigo descreve como realizar vetores espaciais em diferentes sistemas de coordenadas usando o software Perception com um exemplo baseado em um equipamento síncrono permanentemente excitado.
1. Introdução
2. Vetores espaciais
K.P. Kovács desenvolveu a teoria do vetor espacial em 1959 para faciliar uma descrição matemática para sistemas trifásicos. Ela é frequentemente usada para descrever os métodos de controle de motores de indução [4]. As grandezas elétricas e magnéticas de um sistema trifásico podem ser mapeadas para um sistema ortogonal bifásico mais um sistema de seqüência zero, que está presente em determinadas condições. O sistema ortogonal bifásico pode, então ser interpretado como um número complexo que é designado como um vetor espacial. As partes reais e imaginárias do número complexo corresponde às projeções do número complexo apresentado como um vector nos eixos α e β no plano complexo. A equação 1.01 define as regras para cálculo do vetor espacial complexo ![]() de três linhas variáveis x1, x2 e x3:
de três linhas variáveis x1, x2 e x3:
![]()
α é um operador de rotação complexo. O sistema correspondente de seqüência zero é calculado por
![]()
Fig. 2.1a mostra o vetor espacial ![]() num sistema de coordenadas ortogonais..
num sistema de coordenadas ortogonais..
A parte real do vetor espacial aparece na abscissa α, a parte imaginária na ordenada β. Nesta figura, os eixos de coordenadas (α, β) estão em repouso. As quantidades de linhas podem ser obtidas projetando o vetor espacial nos eixos a, b, e c, quando rotacionados em 120º.
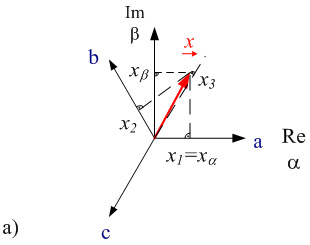
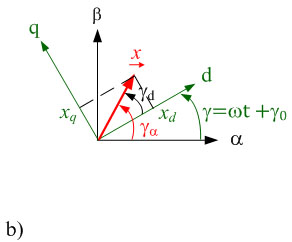
Fig. 2.1: Realização de vetores espaciais no plano complexo a) em sistemas de coordenadas α, com β em repouso e b) nos sistemas de coordenadas rotacionais
O software Perception oferece funções pré-definidas para transformar grandezas trifásicos (x1, x2, x3) em grandezas vetores espaciais:

O software Perception também fornece uma função matemática para a transformação inversa, para o cálculo das grandezas correspondentes da linha de quantidades de espaço de vetores:

Os significados dos vários parâmetros de transferência são claramente descritos na Ajuda on-line, disponível quando as fórmulas são inseridas no Perception.
Utilizando estas funções de transformação, os cálculos podem agora ser feita no domínio de vetor espaciall. Em seguida, os resultados dos cálculos podem ser exibidos de novo como quantidades de linha.
A sobrecarga de computação pode ser reduzida para muitas aplicações, ao mesmo tempo que melhora a clareza dos resultados obtidos se os vetores espaciais são realizados em sistemas de coordenadas rotativas. Até agora, examinamos os sistemas de coordenadas com os eixos α e β em repouso. Agora, iremos também considerar vetores espaciais em um sistema de coordenadas d e q, que é rotacional por um ângulo dependente da função tempo γ(t) em comparação ao sistema de coordenadas α,β original. A derivação das regras de transformação é simplificada se os vetores espaciais são exibidos na tela. O vetor espacial no sistema de coordenadas em repouso é simbolizada como se segue no visor:
![]()
Como mostrado na fig. 1.1b), este vetor espacial também pode ser descrito num sistema de coordenadas de rotação com os eixos d e q. O expoente R indica que o vetor espacial é representado em sistemas de coordenadas rotacionais. No visor, a quantidade não muda em diferentes sistemas de coordenadas. Apenas o ângulo tem de ser ajustado.
![]()
Vetores espaciais são transformados a partir de um sistema de coordenadas para outro, multiplicando-os pelo operador rotacional ejγ.
![]()
A fórmula de Euler ejγ = cos(γ)+j sin(γ) pode ser usada para calcular os componentes do vetor espacial rotacional:
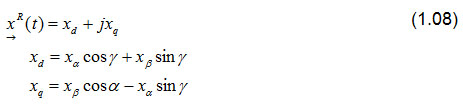
O Perception fornece as seguntes funções para transformar as grandezas de três linhas x1, x2 e x3 em um vetor espacial rotacional.
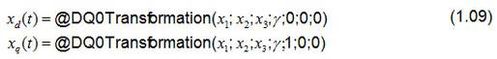
O ângulo y necessário para a transformação é calculado ou lido por um condificador de posição, depedendo de sua aplicação.
3. Máquina síncrona permanentemente excitada
O uso de vetores espaciais em diferentes coordenadas será explicado no exemplo de uma equipamento síncrono permanentemente excitado [4]. Para manter a descrição simples do equipamento, uma equipamento síncrono isotrópico será considerada. Isto significa que o campo magnético pode expandir-se no sentido do equipamento de forma independente. A fig. 3.1a) mostra uma montagem em superfície PMSM. Este tipo de equipamento pode ser considerado como sendo próximo a isotrópico. O número de pares de pólos no equipamento mostrado aqui é p = 2. Para se obter uma descrição amplamente utilizável dos equipamentos, os equipamentos atuais são descritos com modelos, com p = 1 como o número de pares de pólos. O simples modelo de vetor espacial do PSM na fig. 3.1b servirá para estender a descrição. Para fazer isso, devemos levar em consideração a correlação entre a velocidade mecânica n e a frequência elétrica f, onde:

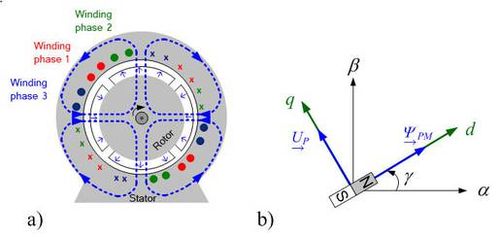
Fig. 3.1: a) Layout básico de um PSM e b) modelo de vetor espacial de um PSM
Se um condificador de posição é colocado sobre o eixo do equipamento de sincronização, o número de pares polares p e um ângulo de desvio γ0 do ângulo γ necessário para a transformação do vetor espacial pode ser calculado. A função
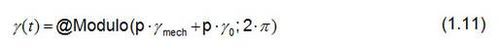
é definida no Perception e usada para este fim. O ângulo de desvio γ0 leva em consideração o desvio mecânico entre o pólo norte do rotor e a posição inicial do codificador de posição.
Um teste sem carga é usado para determinar o ângulo de desvio γ0. Para fazer isso, o equipamento síncrono é acionado mecanicamente pelo eixo. A fig. 3.2 mostra a tensão estrela u1 como uma função de tempo e do ângulo mecânico γmech lido pelo codificador de posição. O ângulo de desvio γ0 pode ser lido a partir do desvio do tempo entre a passagem pelo zero com inclinação negativa da tensão u1 e a posição inicial do codificador de posição.
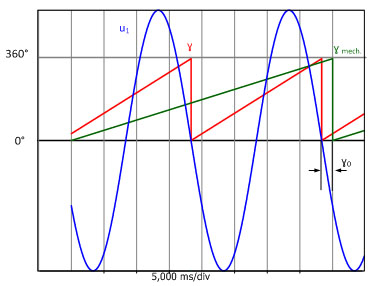
Fig. 3.2: Curva em função do tempo da tensão estrela u1, ângulo mecânico γmech e ângulo elétrico γ
As tensões estrela induzidas no teste sem carga são mostradas na fig. 3.3. Estas três tensões sinusoidais formam um sistema trifásico simétrico, se as amplitudes das tensões são iguais em magnitude e o deslocamento de fase entre as tensões é de 120º. Os componentes do vetor espacial (uα,uβ) pertencentes à esta tensão trifásica também são mostrados na fig. 3.3a como uma função do tempo. Dado um sistema de tensão simétrica, uma mudança de fase de 90º é estabelecida entre os componentes do espaço vetor (uα,uβ).
Se os componentes do vetor espacial são representados num gráfico xy, o pico da tensão do vetor espacial descreve um círculo, como mostrado na fig. 3.3b. Se a trajetória da curva desviar de um círculo ideal, isso poderá ser facilmente notado, já que as três tensões não formarão um sistema trifásico simétrico.
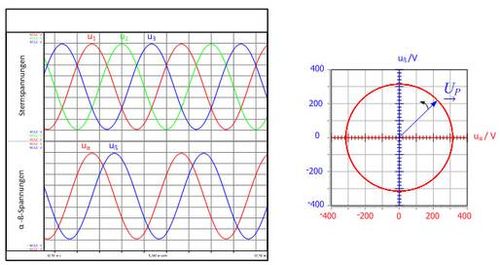
Fig. 3.3: a) Curva em função do tempo das tensões estrela u1,u2 e u3 dos componentes do vetor espacial uα,uβ b) Trajetória da tensão do vetor espacial
Agora, se os componentes de tensão do vetor espacial uα e uβ são mostrados em um sistema de coordenadas rotativas com os componentes ud e uq, estas quantidades, que variam ao longo do tempo, se tornam grandezas constantes. Os componentes ud e uq do sistema trifásico simétrico são mostrados na fig. 3.4, uma vez como uma função do tempo e outra vez no plano complexo. Um sistema trifásico simétrico é representado no plano complexo como um ponteiro em repouso com um comprimento constante.
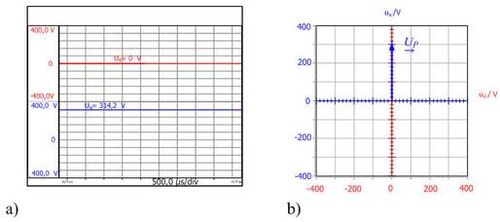
Fig. 3.4: Curva em função do tempo a) dos componentes de tensão do vetor espacial ud e uq e
b) da tensão do vetor espacial no sistema de coordenadas rotativas
Resumo
Este artigo apresenta o condicionamento de sinal com o gravador de dados Genesis HighSpeed e o software Perception usando cálculos de vetores espaciais. As regras de transformação foram descritas para calcular os vetores espaciais em diferentes sistemas de coordenadas, a partir de dados brutos do gravador de dados Genesis HighSpeed. Os sistemas de coordenadas foram apresentados e explicados baseados no exemplo de um teste sem carga com um equipamento síncrono, usando diferentes métodos de exibição para os vetores espaciais com o Perception. Para mais testes práticos dos métodos de cálculo com vetores espaciais em tecnologia de energia, a HBM oferece uma bancada de trabalho rodando com o Perception [3].
Bibliografia
[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft [Electromobility in the fast lane: increased efficiency for the drive of the future]; proceedings of the 3rd conference of Innovation Messtechnik [Innovation in Measurement Technology]; May 14, 2013
[2] Berechnung von Leistungsgrößen mit Perception-Software
[Calculating power values with Perception software] https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/
[3] www.hbm.com
[4] J. Teigelkötter: Energieeffiziente elektrische Antriebe [Energy-efficient electric drives], 1st edition, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3