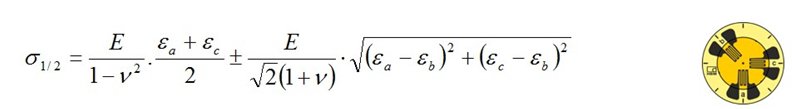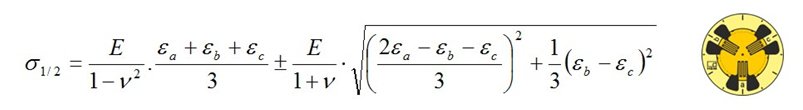Come determinare le sollecitazioni dei materiali partendo dalle misurazioni delle deformazioni
Nell’ambito della deformazione elastica dei materiali i metodi di calcolo delle sollecitazioni dei materiali a partire dalle deformazioni misurate si basano sulla Legge di Hooke. Nella sua forma semplificata, la legge di Hooke è come segue:
σ= ε ⋅ Ε
σ= sollecitazione del materiale [N/mm2]
ε= deformazione [m/m]
Ε= modulo di elasticità, ad esempio modulo di Young [N/mm2]
Questa versione della Legge di Hooke è valida solamente per lo stato di sollecitazione non assiale. Per gli stati di sollecitazione biassiale e multiassiale è necessario utilizzare le versioni più estese.
Nota: Nelle misurazioni delle sollecitazioni è possibile determinare solamente la differenza tra una condizione di output iniziale e una condizione di output successiva. La condizione iniziale può essere senza carichi, ma può anche avere un precarico significativo, dovuto ad esempio al peso proprio dell’oggetto, come nel caso di un ponte.
Le condizioni di precarico o di sollecitazione residua possono essere misurate solamente nel caso in cui venga agevolata l’interferenza con l’oggetto, ad esempio realizzando un foro.
La sollecitazione del materiale s deve essere calcolata dalla deformazione misurata ε solo in accordo alla Legge di Hooke per lo stato di sollecitazione non assiale come nell’equazione riportata in precedenza, se la deformazione ε viene misurata nella direzione attiva della forza (direzione 0°).
Nella direzione trasversale (direzione 90°), non sono presenti sollecitazioni del materiale nonostante la presenza della deformazione misurabile (contrazione trasversale, dilatazione trasversale).
Per questo, per ottenere risultati affidabili, la direzione attiva della forza deve essere nota e la deformazione deve essere misurata in questa direzione. Se questa direzione non è nota o è nota solo in maniera approssimativa, le misurazioni e le relative valutazioni dovranno essere effettuate con lo stato di sollecitazione biassiale nelle principali direzioni non note.
Nei problemi relativi all’analisi sperimentale delle sollecitazioni, lo stato di sollecitazione non assiale è solitamente un’eccezione. Lo stato di sollecitazione biassiale è molto più comune; per determinarne il valore, non è possibile usare il metodo semplice utilizzato per lo stato di sollecitazione non assiale perché sarebbe soggetto a errori.
Per uno stato di tensione piana, le sollecitazioni normali estreme σ1 e σ2 avvengono nelle direzioni perpendicolari 1 e 2. Le sollecitazioni σ1 e σ2 vengono definite sollecitazioni principali, quindi per analogia le direzioni 1 e 2 sono considerate le direzioni principali dello stato di sollecitazione. Se le sollecitazioni normali principali e le direzioni attive corrispondenti sono note, la condizione di sollecitazione biassiale può essere definita in modo preciso.
Le direzioni delle sollecitazioni principali sono note, ad esempio, sulla superficie di un recipiente cilindrico sottoposto a pressione interna, su un albero sottoposto a carichi di torsione pura e nelle zone lontane dagli spigoli e su una lastra curva.
Con altri oggetti e con l’azione simultanea di diverse variabili, come la forza normale e la flessione o la torsione e la flessione ecc., le direzioni principali devono essere considerate non note.
Le sollecitazioni normali principali σ1 e σ2 dello stato di sollecitazione biassiale sono calcolate utilizzando la versione estesa della Legge di Hooke dalle deformazioni principali misurate ε1 e ε2, il modulo di elasticità del materiale E e il coefficiente di Poisson v del materiale:
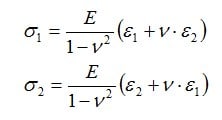
La sollecitazione σ3 nella direzione principale 3 (perpendicolare alla superficie) viene considerata uguale a zero.
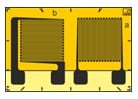
Per semplificare le procedure di montaggio, le rosette X sono adatte per le misurazioni nel campo delle sollecitazioni biassiali con direzioni principali note. Gli assi delle due griglie di misurazione devono essere montate allineate agli assi delle sollecitazioni normali principali (direzioni principali della deformazione).
Per gli oggetti di forma complessa, dove si sovrappongono diversi tipi di carico (carichi normali, di flessione o di torsione) o per i punti di disomogeneità (es. variazioni nella zona a sezione trasversale), in genere non è possibile prevedere le direzioni principali dello stato di sollecitazione.
In tutti i casi in cui le direzioni delle sollecitazioni principali non sono definite chiaramente, l’analisi delle sollecitazioni deve essere effettuata in accordo ai metodi descritti di seguito.