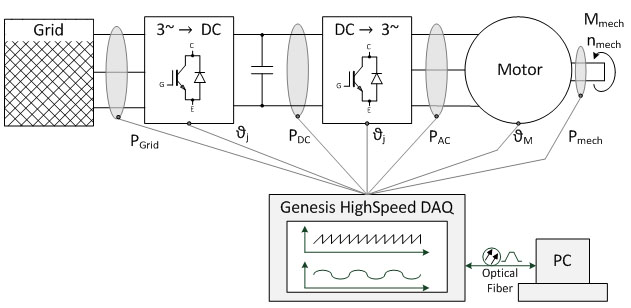
3상 드라이브를 나타내는 그림. 1.1과 같이, 에너지 관련 시스템에서 계측된 다양한 물리량을 기록, 저장, 조절해야 합니다. Genesis HighSpeed data recorders 는 많은 수의 채널과 빠른 샘플링 속도를 이용하여 에너지 관련 시스템에서 상당한 계측량을 동시에 수집할 수 있습니다[1]. 특히 3상 전류가 공급되거나 3상 시스템을 만들어내는 에너지 관련 시스템에서는 공간벡터를 이용하여 계측량을 명확하게 구현함으로써 그 해석이 쉽습니다. 공간벡터는 또한 고정된 작동 상태 및 동적인 밸런싱 프로세스를 표시할 때에도 이용할 수 있습니다. 이 문서에서는 공간벡터 정의 방정식과 다른 좌표계로의 변환 규칙이 먼저 설명됩니다. 그리고 공간벡터를 이용하여 PSM(Permanently excited Synchronous Machines, 영구 자성 동기 장치)의 물리량을 구현하는 방법이 설명됩니다. 이러한 방법들을 독립적으로 시험하기 위해 Perception 워크벤치를 준비했습니다[3].
Calculation and Realization of Measured Quantities in Electrical Energy Technology as Space Vectors with HBM Perception Software
요약
공간벡터는 변압기나 유도 모터와 같은 전기 에너지 변환 시스템에서의 계측량을 명확하고 간결하게 구현할 경우에 자주 이용됩니다. 시간에 따른 공간벡터가 complex plane에서 궤적 곡선(locus curves)으로서 구현되면, 이들 에너지 변환기의 작동 상태에 관한 추가 정보를 결정할 수 있습니다. 이들 계측량을 더욱 간단히 표시하기 위해, 공간벡터를 회전좌표계에서 구현할 수 있습니다. Permanently excited synchronous machine(영구 자성 동기 장치)에 기초한 사례를 통해, Perception software 를 이용하여 공간벡터를 다른 좌표계에서 구현하는 방법을 설명합니다.
1. 소개
2. 공간 벡터
K.P. Kovács는 3상 시스템을 수학적으로 쉽게 설명하기 위해1959년 공간벡터 이론을 개발했습니다. 이 이론은 유도 모터 제어 방법을 설명하는 데 자주 이용됩니다[4]. 3상 시스템의 전기량과 자기량은 특정 조건에서 존재하는 2상 직교 시스템 및 제로-시퀀스 시스템으로 매핑할 수 있습니다. 그 다음, 2상 직교 시스템은 복소수(complex number)로 해석될 수 있는데, 이 복소수가 바로 공간벡터가 됩니다. 복소수의 실수 부분과 허수 부분은 복소평면(complex plane)의 α 및 β 축에 벡터로 표시된 복소수 프로젝션에 해당됩니다. 방정식 1.01은 3개 라인의 변수 x1, x2, x3에서부터 복소 공간벡터 ![]() 를 계산하는 규칙를 정의합니다.
를 계산하는 규칙를 정의합니다.
![]()
대응되는 제로-시퀀스 시스템은 다음과 같이 계산됩니다.![]()
그림. 2.1a는 직교 좌표계에서의 공간벡터 ![]() 를 나타냅니다.
를 나타냅니다.
공간벡터의 실수 부분은 가로축 α에, 허수 부분은 세로축 β에 표시됩니다. 이 그림에서, 좌표축 (α, β)은 고정되어 있습니다. 공간벡터를 축에 투영하고 120° a, b, c 회전시켜 라인의 양 (line quantities)을 얻을 수 있습니다.
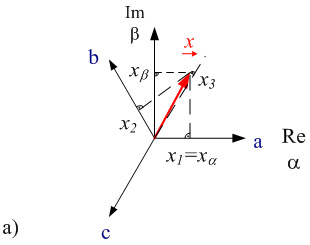
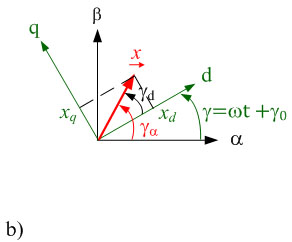
그림. 2.1: 복소평면에서의 공간벡터 구현 a) α, β가 고정된 좌표계 b) 회전좌표계
Perception 소프트웨어에는 3상의 양(x1, x2, x3)을 공간벡터의 양으로 변환시키는 기능이 이미 정의되어 있습니다.:
Perception은 또한 수학적인 역변환(reverse transformation) 기능이 있어, 공간벡터의 양에서 그에 대응하는 라인의 양을 계산할 수 있습니다.

0제, 이들 변환 함수를 이용하여, 공간벡터 영역에서 계산을 수행할 수 있습니다. 그리고 계산 결과는 다시 라인의 양(line quantities)으로 표시할 수 있습니다.

공간벡터를 회전좌표계에서 구현하면 결과의 명확성이 향상되기 때문에, 실제 이용에 있어 계산에 들어가는 비용을 줄일 수 있습니다. 지금까지, α와 β 축이 고정된 좌표계를 살펴보았습니다. 이제, 처음의 α, β 좌표계와 비교하여 시간에 따라 임의 각도 y(t)로 회전하는 d, q 좌표계의 공간벡터에 관해 알아보겠습니다. 공간벡터를 극성 디스플레이(polar display)에서 설명하면 변환 규칙을 도출하기가 간단해집니다. 고정 좌표계에서의 공간벡터는 다음과 같이 극성 디스플레이에 표기됩니다.![]()
그림. 1.1b)와 같이, 이 공간벡터는 또한 d 및 q 축이 있는 회전좌표계에서도 설명될 수 있습니다. 위첨자 R은 공간벡터가 회전좌표계에서 표시된다는 것을 나타냅니다. 극성 디스플레이의 경우, 양(Amount)은 다른 좌표계에서는 변하지 않습니다. 각도만 조절해야 합니다.
![]()
Space vectors are transformed from one coordinate system to another by multiplying them by the rotation operator ejγ.
![]()
Euler's formula ejγ = cos(γ)+j sin(γ) can be used to calculate the components of the rotating space vector.
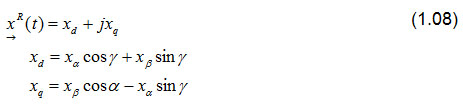
Perception provides the following functions to transform the three line quantities x1, x2 and x3 into a rotating space vector.
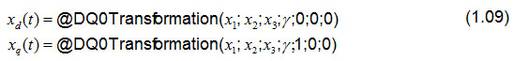
The angle γ required for the transformation is either calculated or read by a position encoder, depending on the application.
3. Permanently excited synchronous machine(영구 자성 동기 장치)
다른 좌표계의 공간벡터를 이용하는 방법은 Permanently excited synchronous machine(영구 자성 동기 장치)를 예로 들어 설명할 수 있습니다[4]. 동기 장치에 관한 설명을 간단히 하기 위해, 등방성 동기 장치(Isotropic synchronous machine)를 고려할 수 있습니다. 이것은 자기장이 장치 안에서 방향에 상관없이 확장할 수 있다는 것을 의미합니다. 그림. 3.1a)는 표면에 장착한 PMSM을 보여줍니다. 이 유형의 장치는 대체로 등방성인 것으로 간주할 수 있습니다. 이 장치에서 극 쌍(pole pairs)의 수는 2(p=2)입니다. 이해를 쉽게 하기 위해, 극 쌍의 수가 1(p=1)인 모델로 설명합니다. 그리고 그림. 3.1b에 표시된 PSM의 단순한 공간벡터 모델을 이용하여 설명을 추가합니다. 이를 위해서는, 기계적 속도 n과 전기 주파수 f 사이의 상관관계를 고려해야 합니다.


Fig. 3.1: a) PSM의 기본 레이아웃, b) PSM의 공간벡터 모델
포지션 인코더를 동기 장치의 샤프트에 배치하면, 극 쌍 p의 개수를 계산할 수 있고, 또한 공간벡터 변환에 필요한 각도 y의 오프셋 각도 y0를 계산할 수 있습니다. 이 기능은 Perception에서 정의되어 이미 사용되고 있습니다.
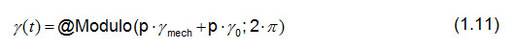
오프셋 각도 y0는 로터(rotor)의 북극과 포지션 인코더의 제로 포지션 사이의 기계적 오프셋을 고려합니다.
오프셋 각도 y0를 결정하는 데에는 무부하 테스트(No-load test)가 이용됩니다. 이를 위해, 동기 장치는 샤프트를 이용하여 기계적으로 구동됩니다. 그림. 3.2에서는 스타 전압(star voltage) u1이 시간 함수라는 것과, 기계 각도 ymech가 포지션 인코더로 판독된 것을 보여주고 있습니다. 오프셋 각도 y0는 전압 u1의 기울기가 음인 제로 크로싱과 포지션 인코더의 제로 포지션 사이의 시간 오프셋을 통해 판독될 수 있습니다.
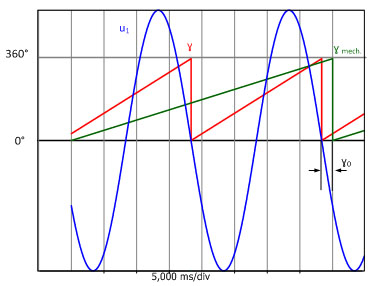
Fig. 3.2: 스타 전압 u1의 시간에 따른 곡선, 기계 각도 ymech 및 전기 각도 y
무부하 테스트에서 유도된 스타 전압은 그림. 3.3에 나와 있습니다. 전압의 진폭 크기가 동일하고 전압 사이의 위상 오프셋이 120°이면, 이들 세 가지 정현파(sinusoidal) 전압은 대칭 3상 시스템을 형성합니다. 이 3상 전압에 속하는 공간벡터 요소 (uα, uβ) 역시 그림. 3.3a에서 시간 함수로 표시되어 있습니다. 대칭 전압 시스템인 것을 감안하면, 공간벡터 요소 (uα, uβ) 사이에 90°의 위상 변화가 생깁니다.
공간벡터 요소가 xy 플롯에 표시되는 경우, 전압 공간벡터의 최대치는 그림. 3.3b에 보이는 바와 같이 원을 그립니다. 곡선의 궤적이 이상적인 원에서 벗어나는 경우, 세 가지 전압이 대칭 3상 시스템을 형성하지 않았다는 것을 바로 알 수 있습니다.
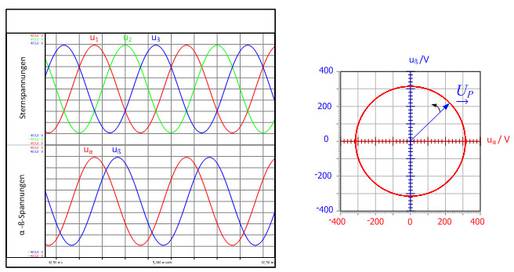
Fig. 3.3: a) 공간벡터 요소 uα, uβ와 스타 전압 u1, u2, u3의 시간 흐름에 따른 곡선 b) 전압 공간벡터의 궤적
이제, 전압 공간벡터의 요소인 uα 및 uβ가 ud 및 uq가 있는 회전좌표계에 표시되면, 시간에 따라 변화하는 이들 양이 일정한 양으로 바뀌게 됩니다. 대칭 3상 시스템의 요소인 ud 및 uq가 그림. 3.4에서 한 번은 시간의 함수로 표시되어 있고, 또 한 번은 복소평면에 표시되어 있습니다. 대칭 3상 시스템은 복소평면에서 길이가 일정한 고정 포인터로서 표시됩니다.

Fig. 3.4: a) 전압 공간벡터 요소 ud 및 uq의 시간 흐름에 따른 곡선 b) 회전좌표계에서 전압 공간벡터의 시간 흐름에 따른 곡선
요약
이 부분은 공간벡터 계산을 이용하는 Genesis HighSpeed 데이터 레코더 및 Perception 소프트웨어에 의해 신호를 조절하는 방법에 관해 설명합니다. Genesis HighSpeed 데이터 레코더의 미가공 데이터로부터 다른 좌표계의 공간벡터를 계산하기 위한 변환 규칙은 이미 설명되었습니다. Perception 소프트웨어를 이용하여 공간벡터를 다른 방법으로 표시하는 동기 장치로 무부하 테스트를 시행했고, 이 일례에 기초하여 좌표계가 설명되었습니다. 에너지 기술 분야에서의 공간벡터 계산 방법을 좀 더 현실에 맞게 테스트하기 위해, HBM은 Perception으로 실행되는 워크벤치를 제공하고 있습니다[3].
참고 자료
[1] D. Eberlein; K. Lang; J. Teigelkötter; K. Kowalski: Elektromobilität auf der Überholspur: Effizienzsteigerung für den Antrieb der Zukunft [Electromobility in the fast lane: increased efficiency for the drive of the future]; proceedings of the 3rd conference of Innovation Messtechnik [Innovation in Measurement Technology]; May 14, 2013
[2] Berechnung von Leistungsgrößen mit Perception-Software
[Calculating power values with Perception software] https://www.hbm.com/de/3783/berechnung-von-leistungsgroessen-mit-perception-software/
[3] www.hbm.com
[4] J. Teigelkötter: Energieeffiziente elektrische Antriebe [Energy-efficient electric drives], 1st edition, Springer Vieweg Verlag, 2013; ISBN 3-8348-1938-3