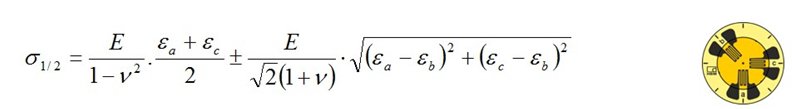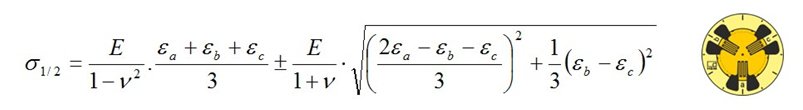Determinación de tensiones de materiales a partir de medidas de deformación
Dentro del rango de deformación elástica de los materiales, los métodos para calcular las tensiones a partir de las deformaciones medidas se basan en la ley de Hooke. En su forma más sencilla, la ley de Hooke se enuncia así:
σ= ε ⋅ Ε
σ= tensión del material [N/mm2]
ε= deformación [m/m]
Ε= módulo de elasticidad o de Young [N/mm2]
Esta versión de la ley de Hooke solo es aplicable a estados de tensión uniaxiales. Los estados de tensión biaxiales y multiaxiales requieren versiones más extendidas.
Nota: Las mediciones de deformación permiten determinar la diferencia entre un estado de salida inicial y un estado posterior. La situación inicial puede ser un estado sin carga, pero también un estado con una precarga considerable, debida por ejemplo al propio peso del objeto, como ocurre en el caso de un puente.
Este estado de precarga o tensión residual (o interna) solo se puede medir mediante una interferencia con el objeto; por ejemplo, perforando un pequeño taladro.
La tensión del material σ solo se puede calcular a partir de la deformación medida ε utilizando la ley de Hooke en el caso de los estados de tensión uniaxiales (ecuación anterior), siempre y cuando la deformación ε se mida en la dirección activa de la fuerza (es decir, a un ángulo de 0°).
En la dirección transversal (a 90°), no existe ninguna tensión en el material, a pesar de que es posible medir una deformación (contracción o dilatación transversal).
Por lo tanto, para obtener resultados fiables es preciso conocer la dirección activa de la fuerza y medir la deformación en esa dirección. Si no se conoce esa dirección (o solo se conoce de forma aproximada), las medidas y su evaluación deben efectuarse en un estado de tensión biaxial, con direcciones principales desconocidas.
En los problemas de análisis experimental de tensiones, los estados de tensión uniaxiales suelen ser más la excepción que la regla. Lo más normal es encontrarse con estados de tensión biaxiales, que no pueden determinarse utilizando el sencillo método de los estados uniaxiales, porque se producirían errores significativos.
En el caso de los aviones, las tensiones normales extremas σ1 y σ2 se producen en las direcciones perpendiculares 1 y 2. Las tensiones σ1 y σ2 se denominan “tensiones principales”; análogamente, las direcciones 1 y 2 se denominan “direcciones principales” del estado de tensión. Si se conocen las tensiones normales principales y sus direcciones activas, el estado de tensión biaxial se puede definir sin ambigüedades.
En algunos casos, las direcciones principales de la tensión son conocidas; por ejemplo, en la superficie de un recipiente cilíndrico sometido a presión interna, en un eje cargado con una fuerza puramente de torsión, o en una placa sometida a flexión (lejos de los bordes).
En el caso de otros objetos, y también cuando actúen de forma simultánea distintas variables, como una fuerza normal y otra de flexión, o una de torsión y otra de flexión, etc., se debe asumir que las direcciones principales son desconocidas.
Las tensiones normales principales σ1 y σ2 de un estado de tensión biaxial se calculan mediante la versión extendida de la ley de Hooke, a partir de las deformaciones principales medidas ε1 y ε2, el módulo de elasticidad del material E y el coeficiente de Poisson ν del material:
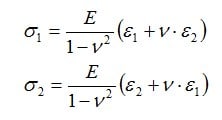
Se presupone que la tensión σ3 en la dirección principal 3 (perpendicular a la superficie) es igual a cero.
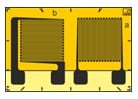
Para simplificar los procedimientos de montaje, se pueden utilizar rosetas en X para medir campos de tensión biaxiales con direcciones principales conocidas. Los ejes de las dos rejillas de medición deben montarse alineados con los ejes de las tensiones normales principales (o sea, en las direcciones principales de extensión).
En el caso de objetos con formas complejas, con superposición de distintos tipos de cargas (cargas normales, de flexión o de torsión) o con zonas no homogéneas (por ejemplo, debido a cambios en la sección transversal), en general no es posible predecir las direcciones principales del estado de tensión.
Si no están claramente definidas las direcciones de las tensiones principales, el análisis de tensiones debe llevarse a cabo siguiendo los métodos que se describen más abajo.