3축 테스트 셀에서 초고성능 콘크리트(UHPC)의 변형 진행에 대한 도량형적 기록
1. 서론과 동기
초고성능 콘크리트(UHPC)는 구조적으로 밀도가 매우 큰 신형 콘크리트이며 강도는 최대 250 N/mm2에 달하여 강철과 버금가는 수준입니다. 초고성능 콘크리트(UHPC)는 일반 콘크리트에 비해 최대 10 배 더 강하며 기존 콘크리트 구조 보다는 경량 구조를 구현하는 혁신적 설계 개념을 요구합니다.
UHPC는 일반 콘크리트와는 차별화된 재료 측면의 장점과 특별한 특성으로 인하여 상당히 적은 고유 중량과 “개방형 구조”를 특징으로 하는 구조 솔루션을 생성 할 수 있습니다. 이러한 유형의 구조는 일반 콘크리트 구조에 비해 동적 여기(excitation)와 피로 하중에 훨씬 더 민감합니다.
UHPC 구조와 같이, 주로 일축 응력은 막대 형태의 구성요소에서 발생하고 다축 응력은 콤팩트 구성요소에서 발생할 뿐만 아니라 집중된 힘이 가해지는 경우에도 발생하는데, 공동연구사업(priority program)의 일환으로 독일 연구 재단(DFG)이 지원한 연구 프로젝트에서는 일축 하중과 3축 하중이 작용할 때 분석과 실험에 기반하여 UHPC의 피로 거동을 연구하는 것을 목적으로 합니다.
이방성 손상이 있는 UHPC에 대한 3차원 기계 모델의 파라미터는 주요 자오선 테스트(회전 대칭 응력, 변형 상태) 결과에 대한 분석을 통해 설정 할 수 있습니다.
2. UHPC에 대한 3차원 기계 모델
2.1. 기본 정보
FEM 프로그램을 사용한 콘크리트, 철근 콘크리트 지지 구조물에 대한 수치 분석을 위해서는 비선형적 재료 응답, 점진적 균열 형성과 손상, 잠재적 고장 상태 등을 실제적으로 설명할 수 있는 적절한 기계 모델이 필요합니다.
표준 강도 콘크리트에 대한 비선형적 재료 응답을 수학적으로 설명하기 위해 개발된 모델의 자세한 개요는[Grünberg/Göhlmann-2005]에서 확인 할 수 있습니다. 파괴 포락선(fracture envelope)은 일반적으로 I1, J2, J3의 불변 함수로서 기하학적으로 설명합니다[Chen-1982].
I1은 정수압 상태를 나타내는 반면에 J2 와 J3은 응력 편차의 성분을 통해 표현합니다.
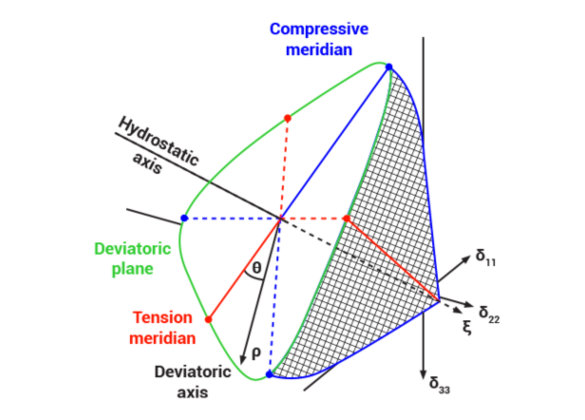
Haigh-Westergaard 좌표 ξ, ρ, θ 를 공식으로 적용하는 것이 유용합니다. 전체 응력 상태 σ 는 정수 응력 성분 ξ, 편차 응력 ρ, 편차 각도 θ에 의해 설명합니다(그림 1 참조).
2.2. UHPC에 대한 3상 모델
기존의 오류 모델은 초고성능 콘크리트(UHPC)에만 제한적으로 적용합니다. 이에 따라, UHPC 에 적용 가능한 3상 모델이 필요하여 개발하였습니다[Grünberg 등. 2007]. 이 모델에서, 취성, 연성 재료 응답은 주 자오선(principal meridians)의 특성 곡선, 특히 파괴 포락선(fracture envelope)의 압축 자오선(compressive meridian)을 통해 설명할 수 있습니다.
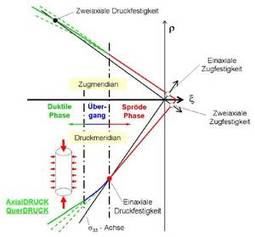
일축 하중의 경우, 초고성능 콘크리트는 장력과 압축에 따른 취성 파괴로 표시합니다. 이 특성은 섬유를 추가해도 변경되지 않습니다. 이러한 취성으로 인하여 장력과 압축 자오선 곡선은 상당히 변경될 것으로 예상합니다. 다축 하중이 작용할 때 이방성 손상이 있는 UHPC의 3 차원 기계 모델을 개발하려면, 압축, 장력 자오선 곡선을 파악하고 있어야 합니다(오른쪽 그림 1 참조).
그림 1: Haigh-Westergaard 좌표(상단), 주 자오선 섹션의 UHPC 3상 모델에 제시된 파괴 포락선
개발된 3상 모델에서, 주 자오선 응력 상태는 특히 흥미롭습니다. 이러한 주 자오선 응력 상태는 축 방향으로 주로 압축 하중을 받는 응력 상태와 회전 대칭 횡응력(횡방향 응력) 상태입니다.
필요한 파라미터를 결정하기 위해, 하노버 라이프니츠 대학의 콘크리트 구조 연구소(Institut für Massivbau)에서 정적, 동적 일축 응력과 3축 응력에 대한 실험적 연구를 실시하였습니다.
3. 실험적 연구
3.1. 압축 자오선 테스트
압축 자오선은 건축 분야의 관행과 관련된 응력비를 적용하는 부분이므로 적용(애플리케이션)을 위해 특히 중요합니다. 낮은 정수압 압축 하중과 축 방향으로 높은 압축 하중 간의 중첩에 의해 생성된 응력비는 3 축 테스트 셀 내에서 연구합니다. 이렇게 연구된 응력비는 압축 자오선에서 확인되며 결과적으로 단축 강도를 상회합니다. 콘크리트에서는 횡압 하중이 낮더라도 축 방향 베어링 강도가 분명하게 증가할 수 있습니다.
연구는 원통형 UHPC 시편(= 60mm)을 사용하여 실시하였습니다. ∅ 로 구성된 “M2Q 혼합물”(h = 180 mm, DFG 공동연구사업1182 “UHPC구조의 지속 가능한 건물”[Schmidt-2008])을 사용하였습니다. [fcm = 198 MPa] 의 강도는 상대적 단축에 대한 연구로 달성하였습니다.
3.2. 3축 테스트 셀과 계측
3축 테스트 셀은 콘크리트의 정적 다축 강도를 파악하기 위해 이미 여러 번 사용하였습니다[Dahl-1992], [Rogge-2002]. 그러나 훨씬 더 중요한 응용분야는 지반 공학, 암석 역학 분야 입니다. 이 시험 장치의 장점은 횡압 하중을 시편에 유압적으로 적용하면서도 축 방향으로의 변형을 막지 않는다는 것입니다.
여기에서 의도한 동적 조사를 위해서는 특수 밀봉 시스템이 요구될 뿐만 아니라 샘플의 위상 동기화 로딩을 특정적으로 제어해야 합니다. 최대 5Hz의 동적 로딩을 위해 설계된 DBTA60-100-RT-DYN 3 축 테스트 셀(그림 2)은 제조업체와의 협력을 통해 개발하였습니다.

그림 2: DBTA60-100-RT-DYN 동적 3축 테스트 셀
압력 챔버(chamber)는 상부 밀폐장치(closure) 안으로 끼워진 스텝 씰(step seal)로 상부 로드 스탬프(load stamp)에 대해 밀봉됩니다. 축 방향 힘은 기존 범용 로딩 프레임의 1MN 실린더에 의해 적용합니다. 횡압은 서보 유압 테스트 장치에 의해 직접 생성되며 Walter & Bai사(社)의 PCS 8000 다중 채널 컨트롤을 통해 5 헤르츠(Hz) 재하 주파수와 위상 동기화되어 구동합니다. 3mm 두께로 제작된 니트릴 부타디엔 고무 샘플 슬리브는 UHPC 시편을 오일로부터 보호합니다.
오일 압력 챔버는 크기가 상당히 대형이므로, 주변의 오일 안에서도 추가적인 측정 기술을 시편에 직접 적용 할 수 있습니다(3.2.3절 참조).
측정 신호는 4-와이어 전기 리드스루(관통부) 8 개를 통해 압력 용기로부터 획득될 수 있습니다. 테스트 셀은 최대 1000 바(bar)의 오일 압력에 대해 설계하였습니다. 셀 안에 있는 기름 양은 특수 알루미늄 패킹을 사용하여 약 8 리터에서 약 1.5 리터까지 줄일 수 있으므로, 횡 방향으로도 “적절한” 정현 하중(sinusoidal loading)을 구현할 수 있습니다.
3.2.1. 테스트 장치와 측정 데이터 획득
3축 테스트 셀은 기존 서보 유압 테스트 장비(그림 3)에 설치되어 새로운 제어 시스템에 통합되고 증폭기에 연결되었습니다.
제조업체의 개별 구성요소(3축 테스트 셀, 유압 & 제어, 측정 기술)를 간단한 테스트 순서에 기초한 테스트 장치에 통합하는 방법은 하노버에 소재한 라이프니츠 대학교 콘크리트 구조 연구소에서 자체적으로 개발하였습니다.

그림 3: 테스트 장비의 3축 테스트 셀
또한, 일부 측정 채널은 제어와 관련되어 있습니다. 그러므로, 우선 이러한 채널(실린더 압력, LVDT, 원주 신장계)을 PCS-8000 제어 시스템으로 기록한 후에 동일 제어 타이밍(0.125ms)에서 아날로그 출력 모듈(0∼10V)을 통해 다시 앰프로 전송해야 합니다. 압력 전송기(횡압)와 레이저 거리 센서에 대해서는 이러한 전환이 필요하지 않은데, 이는 두 시스템에 대한 전압 신호를 병렬로 측정 할 수 있기 때문입니다.
충분한 수의 측정 채널이 기록 될 수 있도록, HBM의 QuantumX MX840B형 범용 앰프 3개를 최대 24개의 사용 가능한 측정 채널로 종속 접속(cascaded) 했습니다. 또한, 이 앰프는 반송 주파수(CF) 풀 브리지 여기(full-bridge excitation)를 지원하므로 전자기 간섭으로부터 보호됩니다. 측정 데이터는 시각화하고 교차 계산된 후에 HBM catman Easy를 사용하여 PC에 기록합니다.
로딩 주파수 5Hz에 대하여, 채널 데이터 속도200 S/s 를 선택하고 Bessel/20Hz로 실시간 필터링하는 과정을 통해 제어 시스템에서도 평탄화된 신호를 획득 할 수 있습니다. 이러한 샘플링 속도를 사용하면 더 오랜 시간 동안 실행되는 테스트(최대 15억 로드 주기)의 누적 데이터량을 적절한 크기와 다양한 형식(bin, ASCII)으로 유지할 수 있는 동시에 피크값(peak)을 적절한 분해능(resolution)으로 기록할 수 있습니다. 스트레인 게이지와 온도 센서는 QuantumX를 통해 독점적으로 획득하였습니다. 시스템이 모듈식 배열을 특징으로 하기 때문에, 연구소에서 다양한 테스트를 위한 효과적인 확장이 가능합니다.
그림 4는 3축 테스트 셀, 계측, 제어 시스템을 활용하는 테스트 설정과 측정 데이터 획득 과정을 도식으로 보여줍니다.
그림 4: 시스템 개요: 3축 테스트 셀, 계측, 제어 시스템, 앰프
사용된 계기, 계기의 특별한 특성에 대한 자세한 내용은 아래 절에 설명되어 있습니다.
3.2.2. 3축 테스트 셀 외부에서 적용되는 측정 기술
축 방향 하중에 사용된 Walter & Bai의 PZ-D 1000/600 서보 유압 테스트 실린더는 최대 ‘’피스톤 스트로크’가 250mm이며 최대 1MN의 하중을 적용 할 수 있습니다. 실린더 변위는 HBM의 LVDT WA200 유도 변위 변환기를 통해 기록되며 측정 범위는 ±200 mm 입니다. 실린더와 구형 캡 사이에 있는 로드셀은 측정 범위가 ±1000kN입니다.

그림 5: 3축 테스트 셀 외부에서 적용되는 측정 기술
P2VA1 압력 변환기(D-1)는 압력 챔버 상단 영역에서 외부로부터 3축 테스트 셀에 나사로 고정되어 오일 압력(최대 1000bar)을 기록하며 전압 신호 (0.5∼10V)를 반환합니다. 일부 테스트에서는 측정 범위가 최대 500bar인 P5MA 절대 압력 변환기(D-2)를 하단 셀 입구에 추가적으로 사용했습니다. 이 측정 신호는 QuantumX 증폭기를 통해 직접 수집하였습니다. 이를 통해 압력 변환기의 측정 신호를 모니터링(중복) 할 수 있는 반면에 이 두 번째 압력 센서를 사용하여 동적 로딩 동안에 압력 챔버에서 위상 천이(phase shift)가 발생하는지를 확인할 수 있습니다.
완전 3축 테스트 셀이 설치된 테스트벤치와 구형 실린더 캡 사이의 거리는 레이저 거리 센서 3 개(L-1 ~ L-3)로 등록합니다. 사용된 센서는 측정 범위가 16mm ~ 26mm이고 분해능은 5 µm 이며 이러한 측정 범위에 대하여 전압 신호(0 ~ 10V)를 반환합니다. 특히 동적 연구에서 레이저 거리 센서는 기계적 구성요소가 없으므로 마모 없이 상당한 수의 부하 주기를 견딜 수 있다는 장점을 보유합니다. 레이저 거리 센서를 통해 측정된 변형 데이터는 시편의 순수한 변형뿐만 아니라 의 비선형적 시작(startup) 효과와 상단, 하단의 하중 스탬프 변형에 관련된 내용을 포함합니다.
이러한 추가적이고 때로는 비선형적인 변형에 관련된 내용을 제외하기 위해, 계기를 오일 안 에서 시편 위에 직접 올려 놓아야 합니다.
3.2.3. 3축 테스트 셀 내부에 적용되는 측정 기술
종방향 변형률과 횡방향 변형률은 샘플 실린더 중앙에 있는 원주 신장계와 각각 120°로 상쇄(offset)된 차동 변압기 3개를 사용하여 시편에서 직접 측정합니다.
변형의 진행을 기록하는 또 다른 방법은 UHPC 시편에 적용된 스트레인 게이지(SG)를 사용하는 것입니다. 여기에서 특별한 측면은 스트레인 게이지가 최대 1000 bar의 주변 압력에 직접 노출된다는 것입니다.
셀 커버 안에 있는 내압 전기 리드스루(4-핀 Lemo S0 4) 8개를 통해 셀 내에서 다양한 측정 기기를 유연하게 사용할 수 있습니다.
차동 변압기 회로(LVDT)의 유도 변위 트랜스듀서
세 가지 LVDT(LVDT-1, LVDT-2, LVDT-3)용 클램핑 장치를 사용하면 샘플의 축 방향 변형을 시편에 매우 가깝게 측정 할 수 있습니다. 제조업체에 따르면 LVDT는 최대 1000bar의 오일 압력에서 사용할 수 있으며 측정 범위는 ± 5 mm 입니다. 클램핑 링은 상단 로드 스탬프 위에 놓인 시편에 가깝게 위치하고 있으며 측정 범위가 초과되면 LVDT를 보호하기 위해 120° 씩 증가하는 플런저용 자기 리테이너(magnetic retainer)를 포함하고 있습니다(좌측 그림 6 참조).

그림 6: 3축 테스트 셀, 계기의 내부 설정
원주 신장계
원주 신장계는 압력 용기 내부에서 사용하도록 설계되었고 광유(최대 1350 bar)를 압력 매체로 사용합니다. 원주 신장계를 사용하면 원통형 콘크리트 샘플의 둘레 변화를 측정 할 수 있습니다. 원주 신장계는 고정밀 특수 롤러 체인에 의해 샘플에 직접 부착합니다. 전체 장치는 일체형 스프링을 통해 자동으로 고정합니다.
영점은 기계식 설정 나사를 사용하여 간단하게 조정할 수 있습니다. 클립의 전체적인 측정 범위는 스트레인 게이지 풀 브리지에 기초한 측정 원리를 적용하여 12mm (-2mm ~ + 10mm) 입니다. 분리 장치는 시편이 갑자기 파손되는 경우 원주 신장계의 파괴를 방지합니다.
탄성 MBR 샘플 슬리브에 의해 측정 결과가 변조되는 것을 방지하기 위해, 테스트에서는 시편의 중앙 영역에 원주 신장계가 배치된 상태에서 매우 얇고 투명한 불소 중합체 수축 조립(shrink-fit) 배관을 사용하였습니다(좌측 그림 6 참조).
스트레인 게이지
이전에 설명한 측정 방법은 모두 샘플의 전체 둘레와 높이에 대한 적분 측정 방법에 해당하는 반면, 스트레인 게이지는 변형의 국부적 진행을 관찰하기 위해 사용할 수 있습니다. 여기에서, 스트레인 게이지를 사용할 때 시편을 준비하여 셀에 통합하는 프로세스에는 훨씬 더 많은 시간과 비용이 소요된다는 점에 유의하는 것이 중요합니다.
이러한 프로세스에서는 측정 그리드 길이가 20mm인 HBM LY41-20/120 스트레인 게이지를 사용합니다. 표면을 다소 거칠게 처리하고 청소한 후, HBM LY41-20/120 스트레인 게이지를 X60접착제와 함께 콘크리트에 적용합니다. 시편을 MBR 슬리브에 삽입 할 때에는 연결 케이블이 더 많이 로드 되므로, 납땜 단자(LS 5)도 사용합니다. 필요에 따라, 최대 3 개의 스트레인 게이지를 수직(SG-l), 수평(SG-t)으로 배치 할 수 있습니다. 연결 케이블은 샘플 슬리브 내부로 연결되어 슬리브 상단의 오일 챔버에 도달합니다(그림 7).
활성 ¼ 브리지는 보상 스트레인 게이지에 의해 하프 브리지(half bridge)까지 확장합니다. 또한, 보상 스트레인 게이지는 셀의 오일이 충전된 압력 챔버의 UHPC 시편 위에 배치합니다. 테스트 동안, 두 스트레인 게이지는 주변을 순환하는 오일에 의해 동일하게 가열합니다. 예비 테스트 결과는 횡압이 측정 값에 영향을 거의 미치지 않는 것으로 나타났습니다. 스트레인 게이지 측정은 정적 테스트에서 매우 신뢰적으로 이루어지지만, 동적 횡압 하중을 적용하면 스트레인 게이지 아래의 표면 근처에 있는 미세 공극으로 인하여 스트레인 게이지 고장 빈도가 증가(3.2.5절 참조)하는데 이는 이전에는 관찰되지 않았던 현상입니다(그림 7, 우측 참조).

그림 7: 스트레인 게이지를 적용한 경우
온도 센서
캡슐화된 Pt100 센서(저항 온도계)를 온도 센서로 사용하여, 압력 챔버 안의 오일 온도를 기록했습니다. 동적 로딩으로 인하여 압력 챔버의 안의 오일을 약 50 °C까지 가열합니다. 테스트 장비의 3축 테스트 셀 바로 옆에서, 추가적인 Pt100 센서를 통해 주변 온도를 기록하였습니다. 저항기는 앰프 연결을 위해 하프 브리지(half bridge)까지 확장되었습니다.
3.2.4. 정적 테스트 결과
정적 테스트는 항상 동일한 패턴을 따라 실행하였습니다. 첫 번째 단계에서는 원하는 횡압(여기에서는 200 bar = 20 N/mm²)에 도달 할 때까지 정수압 응력을 증가시킨 후에 파단(여기에서는 287.1 N/mm²)될 때까지 일정한 실린더 전진 속도로 축 방향 로딩을 진행했습니다. 시간의 경과에 따른 축 방향 응력과 횡압은 그림 8에 제시되어 있습니다.
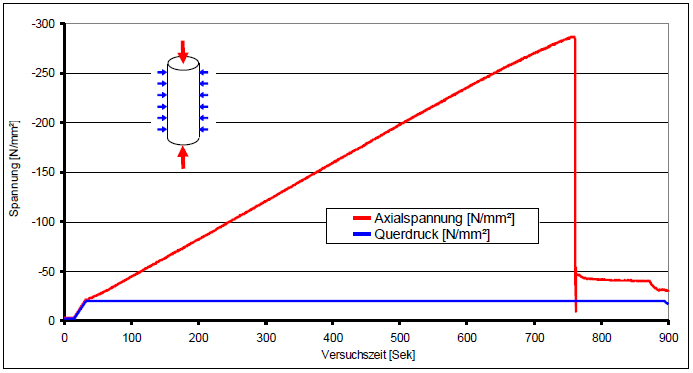
그림 8: 축 방향, 횡 방향 응력 곡선
신장계, 레이저 거리 센서를 사용하여 광범위한 일련의 테스트를 실행했습니다. 그림 9 (좌측)는 UHPC 시편에서 스트레인 게이지를 통해 결정된 축 방향, 횡 방향 변형을 보여줍니다. 비교를 위해, LVDT에서 결정된 축방향 변형률과 원주 신장계에 의해 정의된 횡방향 변형률을 그림 9의 우측에서 확인할 수 있습니다. LVDT의 측정값은 하중 스탬프의 강철 변형을 계산하는 과정을 통해 감소하였습니다.
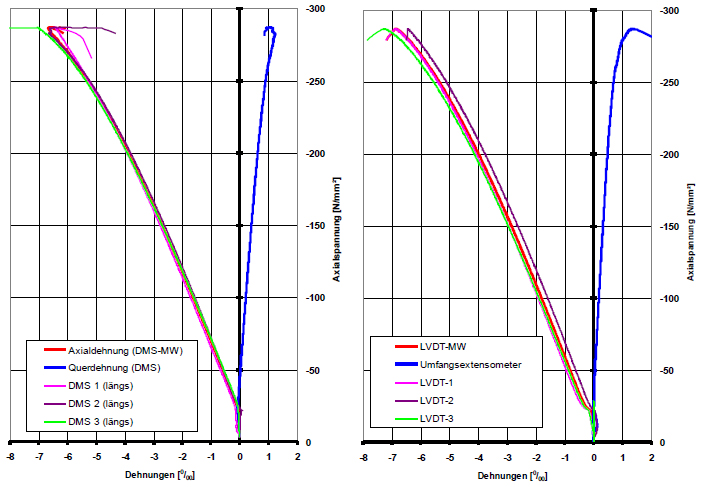
그림 9: 스트레인 게이지(좌측), LVDT(우측)의 변형률 곡선
파단이 발생할 때 두 측정 방법 모두에서 거의 동일한 축 방향 응력을 생성하였습니다(εB ≈6.8 0/00). LVDT를 사용한다면, 초기 정수압 로드 시작을 뒤따라 작은 비선형적 시작(startup) 효과가 뚜렷하게 나타납니다. 이는 상단, 하단 하중 스탬프가 시편을 누르기 때문에 결과적으로 발생합니다. 스트레인 게이지는 시편 변형률을 전적으로 기록합니다.
테스트벤치와 축 실린더의 힘 플레이트 사이에서 레이저 거리 센서(그림 10)를 사용하는 변형 측정 시에는 테스트 설정에 따른 훨씬 더 많은 영향이 관여됩니다. 여기에는 축 방향 하중의 증가에 따라 감소하는 비선형적 시작 효과의 내용뿐만 아니라 강철 하중 스탬프의 탄성 내용과 테스트 설정에 따른 선형적 변형 내용을 포함합니다.
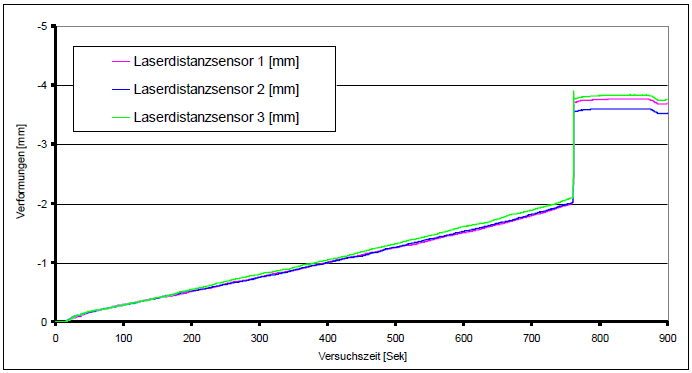
그림 10: 레이저 거리 센서를 통한 변형 측정
3.2.5. 동적 테스트 결과
패킹으로 인하여, 동적 로딩 중에는 내부에서 다른 모든 계기를 사용할 수 없습니다. 그러므로, 이러한 테스트에서는 시편에서 발생하는 변형의 진행을 직접 기록하는 유일한 방법은 스트레인 게이지를 사용하는 것입니다. 문제는 이러한 테스트에서 부하 주기 수가 증가함에 따라 스트레인 게이지에 오류가 발생한다는 것입니다.
다양한 최대 응력(75%,..., 50%)에 대해 실행되는 동적 테스트에서는 항상 일정한 최소 응력(5%) 수준을 적용합니다. 기준 수치는 정적 3축 응력이 작용할 때 특정 파단 하중에 상응합니다. 그림 11은 최대 응력이 55 % 수준인 테스트의 경우 21,558개의 하중 주기(load cycle) 완료 후 파단이 발생될 때까지 전체 주기 수에 대하여 각 하중 주기에 대한 최소, 최대 변형율을 보여줍니다. 중간 오류는 수직선으로 확인 할 수 있습니다(측정 값 "-8‰"). SG-1은 횡방향 변형률을 나타내고 SG-2와 SG-3은 축방향 변형률을 나타냅니다.
횡방향 변형률을 살펴보면, 여기에서 최대 약 3500개의 하중 주기(포인트 1)에 대한 변형률은 예상 곡선과 항상 일치합니다(축방향 변형률의 약 20%). 그렇기 때문에, 값은 “표류(drift)”하고 변형률 차이는 일정하게 유지됩니다. 겨우 5000 주기가 완료되면, 스트레인 게이지에 결국 오류가 발생합니다.
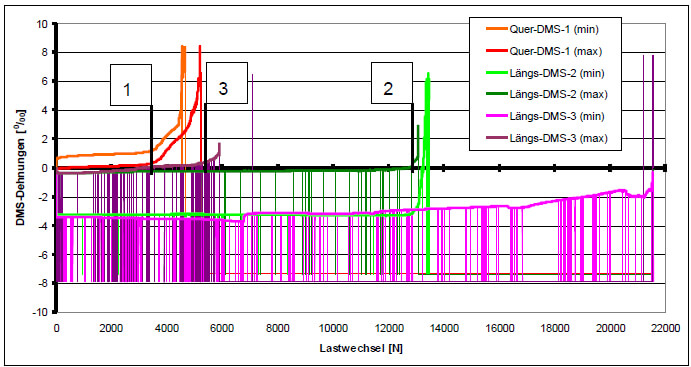
그림 11: 동적 로딩 중의 스트레인 게이지 측정 값
SG-2는 몇 가지 오류가 있더라도 실제 측정 값을 최대 약 13,000로드 주기(포인트 2)까지 반환합니다. 최소 응력 수준에서 SG-3에 대한 변형률 값은 약 5000로드 주기(포인트 3)까지 SG-2에 대한 변형률 값과 잘 일치합니다. 그렇기 때문에, 최소 응력 수준(시편의 최소 압축 수준)에서 SG-3은 측정값을 더 이상 반환하지 않는 반면에 최대 압축 수준에서 동일 스트레인 게이지는 파단이 발생할 때까지 타당한 값을 반환합니다.
스트레인 게이지에 오류가 발생하면, 동적 테스트에서 나머지 최종 측정량(measurand)은 3축 테스트 셀 외부의 레이저 거리 센서를 통해 제공합니다.
측정값 곡선(그림 12)에서는 피로 하중이 작용할 때 콘크리트에서 발견되는 변형의 특징적 진행을 확인할 수 있습니다.
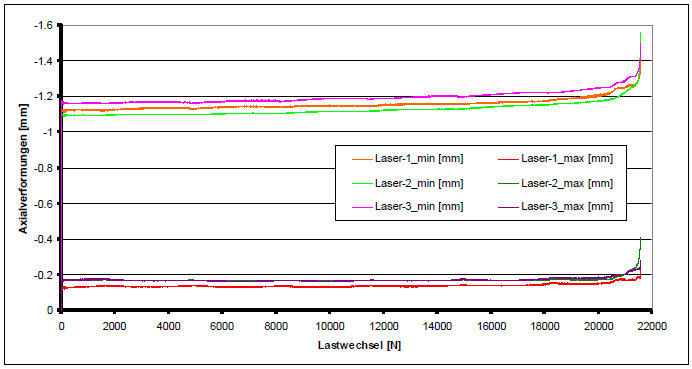
그림 12: 동적 로딩 동안 레이저 거리 센서를 통한 변형 측정
4. Summary and Perspective
With the "triaxial cell" test rig described above, it is possible to determine the triaxial strengths for both static and dynamic loadings.
The use of sensors in the oil-filled pressure chamber of the triaxial test cell is particularly demanding of the measurement technology deployed. By using special inductive displacement transducers (LVDTs) and a circumferential extensometer, it is possible to determine the deformations in static loading directly on the UHPC test specimen. These deformations were verified by strain gages applied directly to the test specimen. For major test series, this saves cost (the material costs of the strain gages) and time in preparing the test specimen (attaching the strain gages).
The problem is metrologically recording the development of the deformation in the dynamic investigations. Because packing is required, it is only possible to use strain gages here. The repeated dynamic loading vertically onto the surface of the strain gage pushes the strain gage into the tiny air voids in the concrete. This eventually causes the strain gage to fail prematurely. Laser distance sensors attached outside the test cell record the characteristic curve of deformation development.
Triaxial tests showed that the three-phase model that has been developed, describes the compressive meridian of the fracture envelope rather well. A transverse pressure loading produces a more ductile material response in the UHPC, compared to the brittle qualities in uniaxial loading.
A detailed report on the ongoing triaxial dynamic investigations and the Wöhler lines that are developed from them, will be given at the 3rd fib-Congress [Ertel/Grünberg-2010].
Acknowledgements & References
Acknowledgements
The research project is supported by the German Research Foundation (DFG) in Priority Program 1182: "Sustainable building with UHPC".
References
[Chen-1982] Chen, W. F.:Plasticity in Reinforced Concrete. McGraw-Hill, New York, 1982.
[Dahl-1992] Dahl, Karre K. B.; The Calibration and Use of Triaxial Cell, Danmarks Tekniske Hojskole, 1992
[Düsterloh 2007] Düsterloh, U.: Triaxiale Kompressionsversuche an UHPC-Beton, Bericht (unveröffentlicht), Institut für Aufbereitung und Deponietechnik, Professur für Deponietechnik und Geomechanik, Technische Universität Clausthal, 2007
[Ertel/Grünberg-2010] Ertel, Chr.; Grünberg, J.: “Triaxial Fatigue Behaviour of Ultra High Performance Concrete”; 3rd fib International Congress; May 29 – June 2, 2010, Washington, D.C. (accepted)
[Grünberg/Göhlmann-2005] Grünberg, J.; Göhlmann, J.: Versagensmodelle für Beton unter monotoner Beanspruchung und Ermüdung. Bauingenieur, Band 80. März 2005
[Grünberg et al. 2007] Grünberg, J., Lohaus, L., Ertel, C. Wefer, M.: Mehraxiales mechanisches Ermüdungsmodell von Ultra-Hochfestem Beton – Experimentelle und analytische Untersuchungen, Beton- und Stahlbetonbau, Heft 6, 2007
[Grünberg et al. 2008] Grünberg, J., Lohaus, L., Ertel, C. Wefer, M.: Multi-Axial and Fatigue Behaviour of ultra–high–performance concrete (UHPC), Proceedings of the 2nd International Symposium on Ultra-High Performance Concrete, 05.-07.03.2008, Kassel
[Kupfer-1973] Kupfer, H.: Das Verhalten des Betons unter mehraxialer Kurzzeitbelastung unter besonderer Berücksichtigung der zweiaxialen Beanspruchung. DAfStb, Heft 229, Ernst & Sohn, Berlin, 1973.
[Rogge-2002] Rogge, Andreas; Materialverhalten von Beton unter mehraxialer Beanspruchung, Dissertation, Lehrstuhl für Massivbau, TU München, 2002.
[Schmidt-2008] Sachstandsbericht Ultrahochfester Beton, Deutscher Ausschuss für Stahlbeton, Heft 561, Beuth, 2008