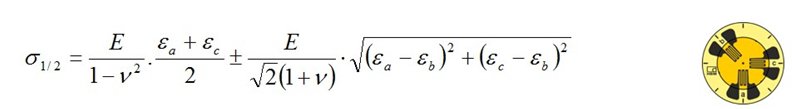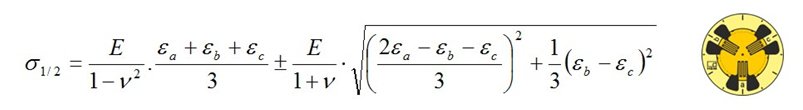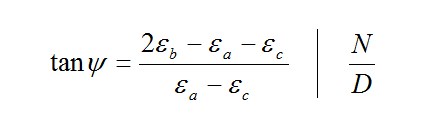ひずみ計測による材料応力の決定
ひずみ計測値から材料応力を計算する方法は、材料の弾性変形範囲内では、フックの法則に基づいて行います。最も単純なフックの法則は次の式で表せます:
σ= ε ⋅ Ε
σ= 材料応力 [N/mm2]
ε= ひずみ [m/m]
Ε= 弾性係数、またはヤング率 [N/mm2]
このバージョンのフックの法則は、一軸応力状態にのみ適用されます。二軸および多軸の応力状態には拡張バージョンが必要です。
注:ひずみ計測では、最初の出力条件とその後に生じる条件との間の差異のみを決定できます。最初の状態は無負荷状態か、もしくは橋のように自重のために大きな予備荷重がかかっている状態の場合があります。
予備荷重または残留応力は、対象物に対して干渉が許容される場合(例えば、ドリルで小さな穴を開ける)にのみ計測することができます。
ひずみεが応力の有効方向(0°方向)で計測された場合、上述の式のような一軸応力状態のフックの法則に従って、計測されたひずみεのみから材料応力σを計算できます。
横方向(90°方向)には、計測可能なひずみ(横収縮、横断方向拡張)があるにもかかわらず、材料応力は存在しません。
したがって、信頼性の高い結果を得るには、力の有効方向を知る必要があり、ひずみをこの方向で計測する必要があります。この方向が不明であるか、またはおおよその方向しかわかっていない場合は、未知の主方向の二軸応力状態で計測とその評価を行う必要があります。
応力解析の問題では、一軸応力状態はむしろ例外的です。二軸応力状態が、はるかに一般的で、ひずみの決定は一軸応力状態に使用される単純な方法で行われるべきではありません。さもないと、大きな誤差の原因となります。
平面応力状態では、垂直応力σ1 及びσ2 が、 垂直方向1及び2で発生します。この応力σ1 およびσ2 は主応力と呼ばれ、同様に、応力状態の主方向の1及び2と呼ばれます。主応力とその有効方向が分かっている場合、二軸応力条件は明確に定義されます。
既知の応力主方向には、例えば、内圧がかけられた円筒形の容器の表面、純ねじりが負荷されたシャフト上、曲げられたプレート上の縁から離れた領域などにかかる応力方向があります。
他の物体との組み合わせ、異なる変数が重なっている場合(垂直応力と曲げ、あるいは、ねじれと曲げが重なっている場合)などでは、主方向は未知であると仮定すべきです。
二軸応力状態の主応力σ1 とσ2は、フックの法則の拡張バージョンにより、計測された主ひずみε1とε2、材料の弾性係数E及びポアソン比νから計算されます:
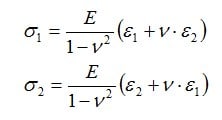
ここでは、主方向3(面に垂直な方向)の 応力σ3 が ゼロに等しいと仮定されます 。
取り付け手順を簡素化するために、Xロゼッタは、既知の主方向を有する二軸応力表面における計測に適しています。2つの計測グリッドの軸は、主応力(主ひずみ方向)の軸に合わせて取り付ける必要があります。
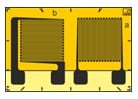
様々な種類の荷重(垂直、曲げ、ねじり荷重)が重なる場合や、または不均一な箇所(例えば、断面積の変化)がある複雑な形状の物体では、応力状態の主方向の予測は一般に不可能です。
主応力方向が明確に定義されていない場合は、以下の方法に従って応力解析を実施する必要があります。