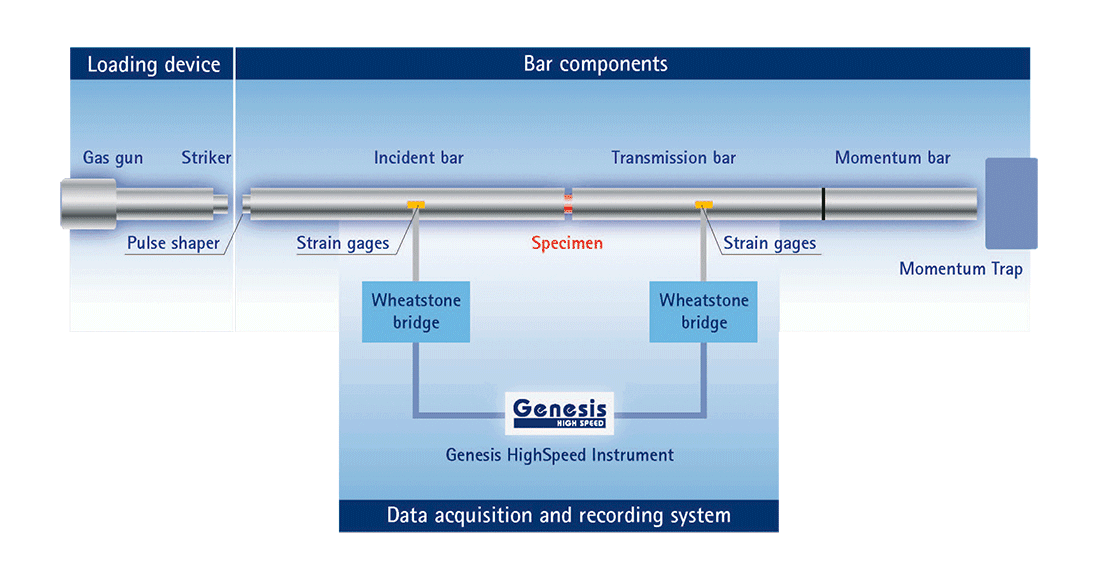
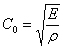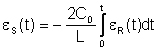Strain gages measure pressure waves
Normally a simple material testing machine is not able to apply the required high strain rates. Therefore, a so-called split-Hopkinson bar is used for measuring such dynamic quantities. British electrical engineer Bertram Hopkinson first suggested such measurements in 1914. The setup used today is based on a modification developed by Herbert Kolsky in London in 1949. It is sometimes also called split-Hopkinson Kolsky bar.
The material sample is positioned between two bars in the split-Hopkinson bar: the incident bar and the transmission bar. A so-called striker - for example, a projectile accelerated by compressed air - strikes the incident bar causing a pressure wave. This pressure wave runs through the first bar. Part of the wave is reflected at the bar end, the other part runs through the material sample into the transmission bar. Strain gages (SG) installed on the surfaces of the incident bar and the transmission bar measure the strains caused by the pressure waves. This enables the amplitudes of the pressure wave originally applied to the incident bar, of the reflected pressure wave and of the transmitted pressure wave to be determined. The strain gages are interconnected in Wheatstone bridge circuits. Since the pressure waves run through the bars at the speed of sound, a very dynamic measurement system is required offering a correspondingly high bandwidth of about 100 kHz.