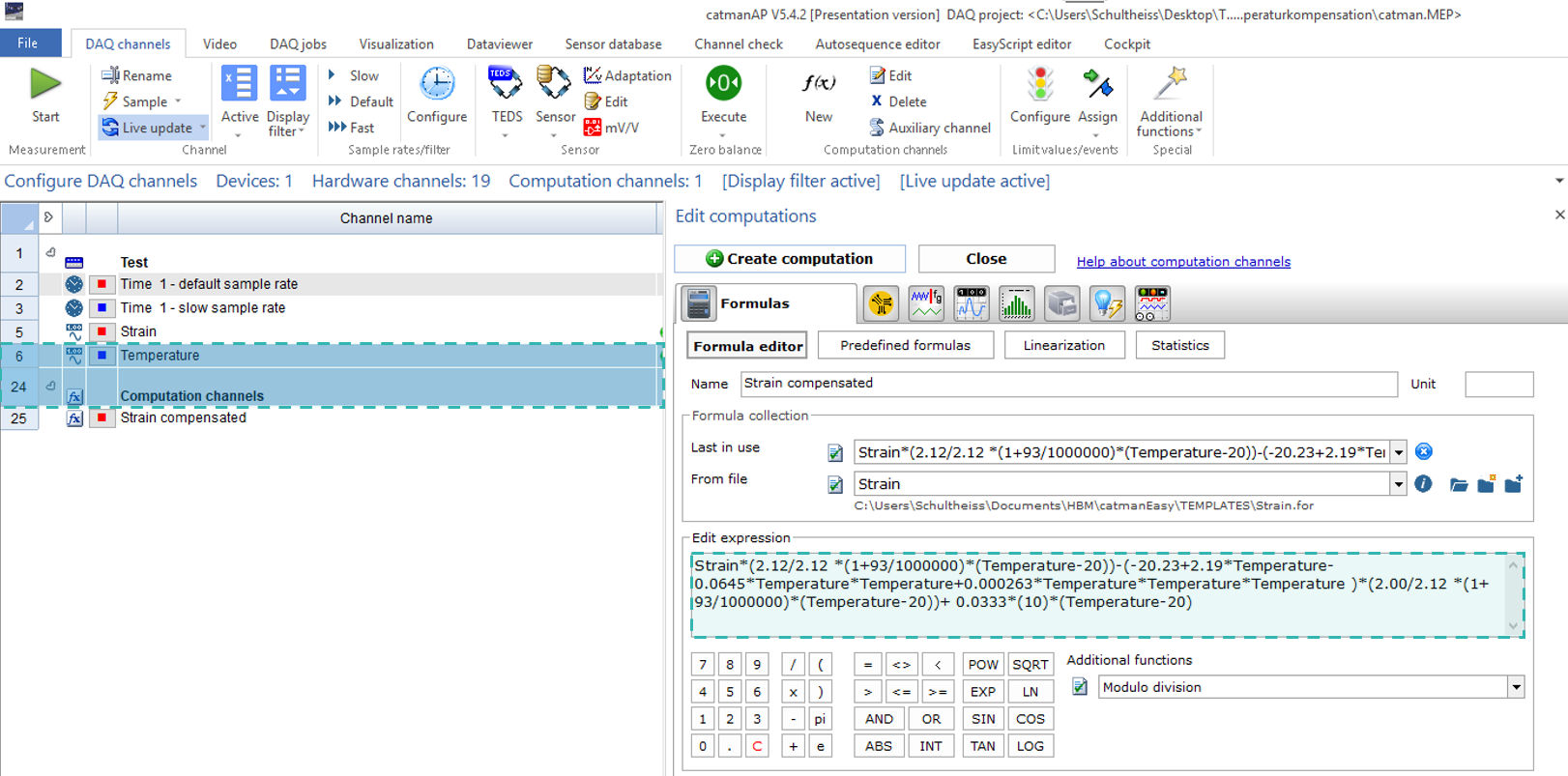
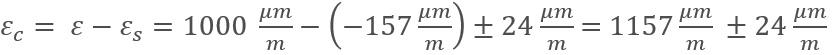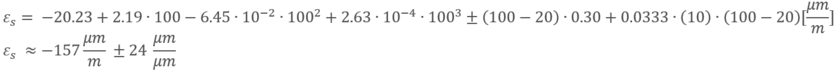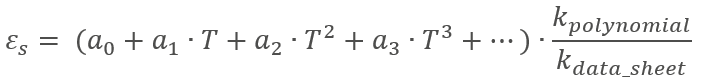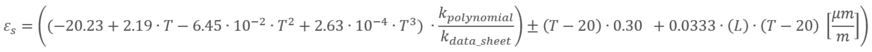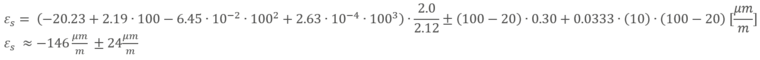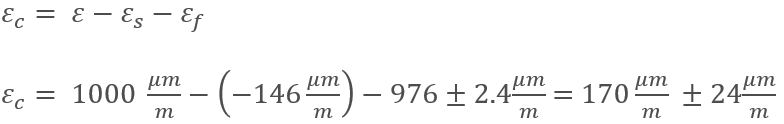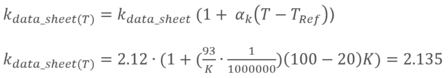En algunos casos, el polinomio incluye otras contribuciones que influyen en la señal de deformación si la temperatura cambia:
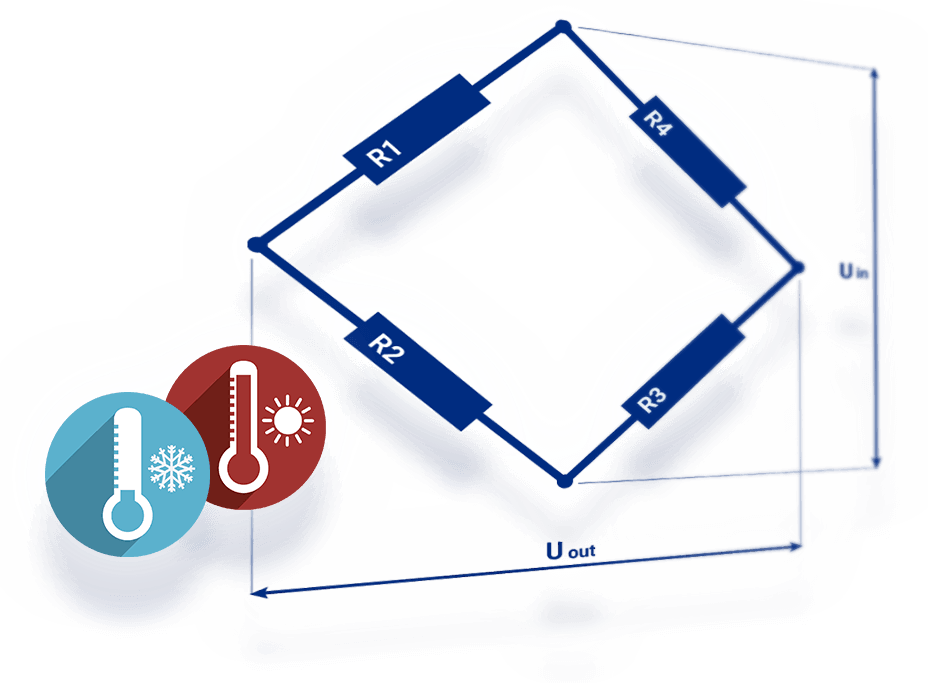
- Influencia de los cables (ε l): En este ejemplo concreto se añade también la incertidumbre de medición y la influencia de los cables de 2 hilos que se conectan a la rejilla de medición de la galga extensométrica. Por norma general, debe tenerse en cuenta la influencia de los cables, pero puede variar según el tipo de galga extensométrica y el fabricante del cable. La Cómo compensar correctamente la resistencia de los cables d compensa todas las resistencias de los cables, si bien en algunos casos hay una parte residual de 2 hilos que no se puede compensar automáticamente.
- Incertidumbre de medición (ε u): La incertidumbre de medición es una componente general que debe considerarse en el cálculo total. Incluso el polinomio tiene una cierta dispersión que genera esta componente de incertidumbre.
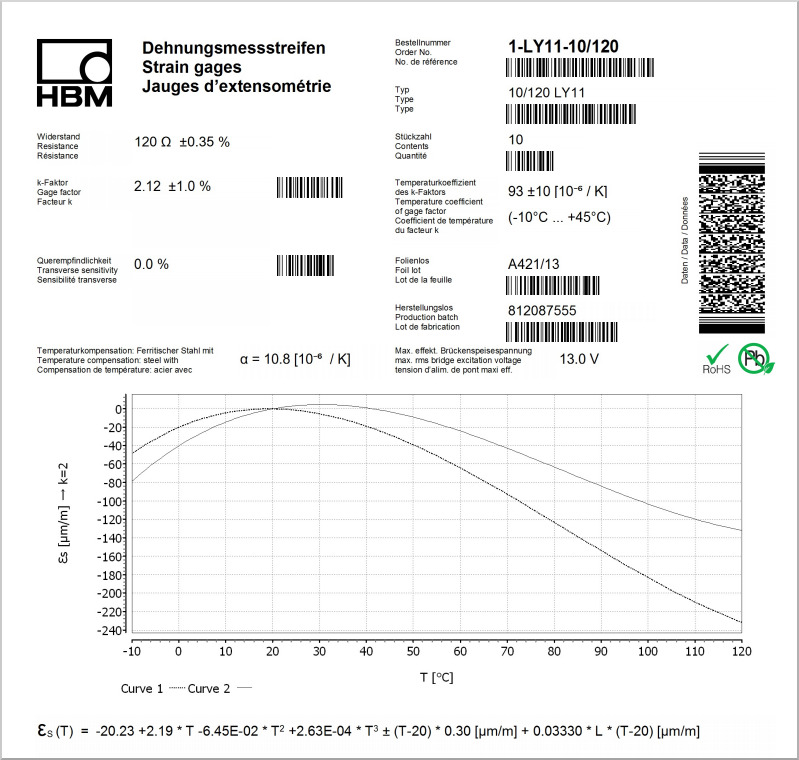
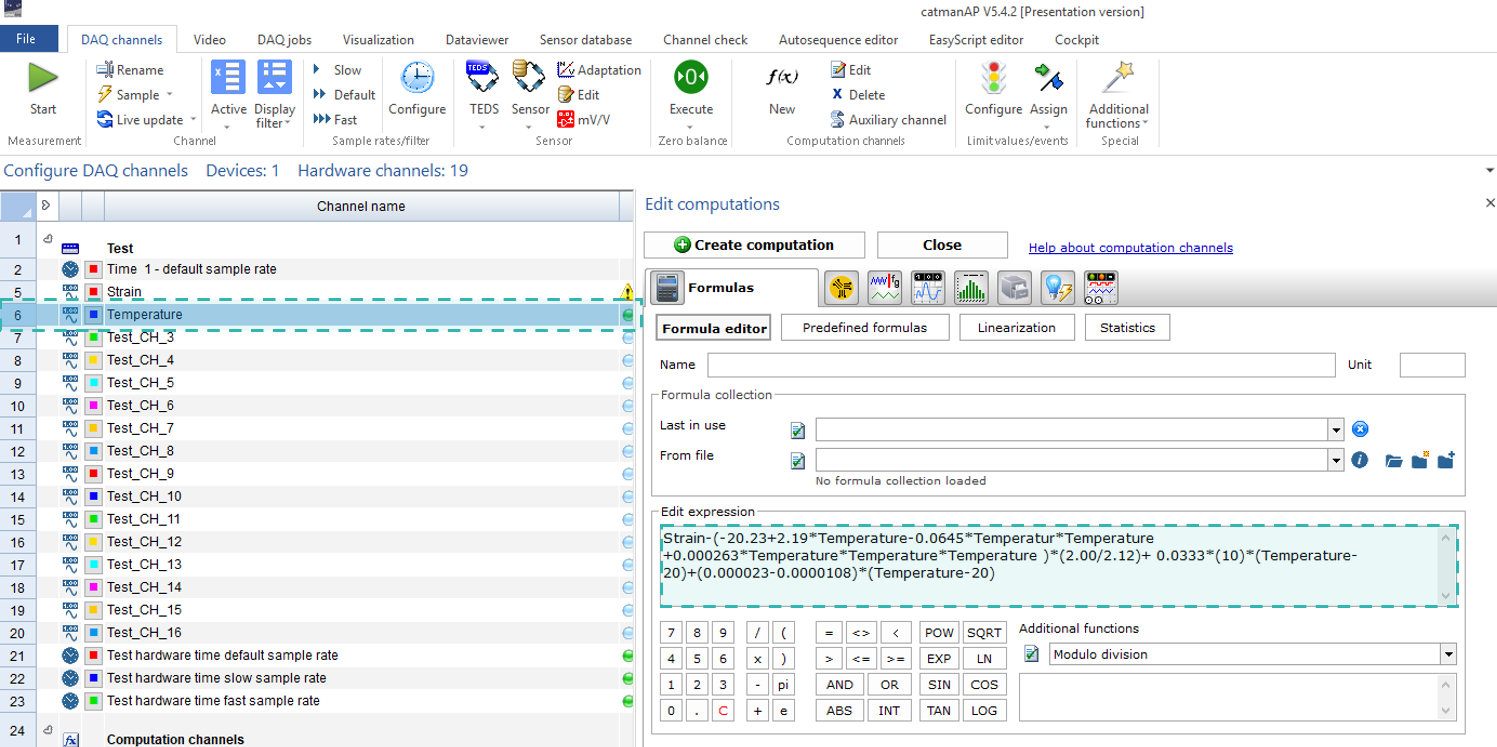
El polinomio adaptado es el siguiente:
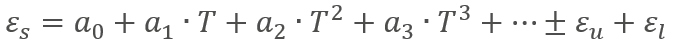
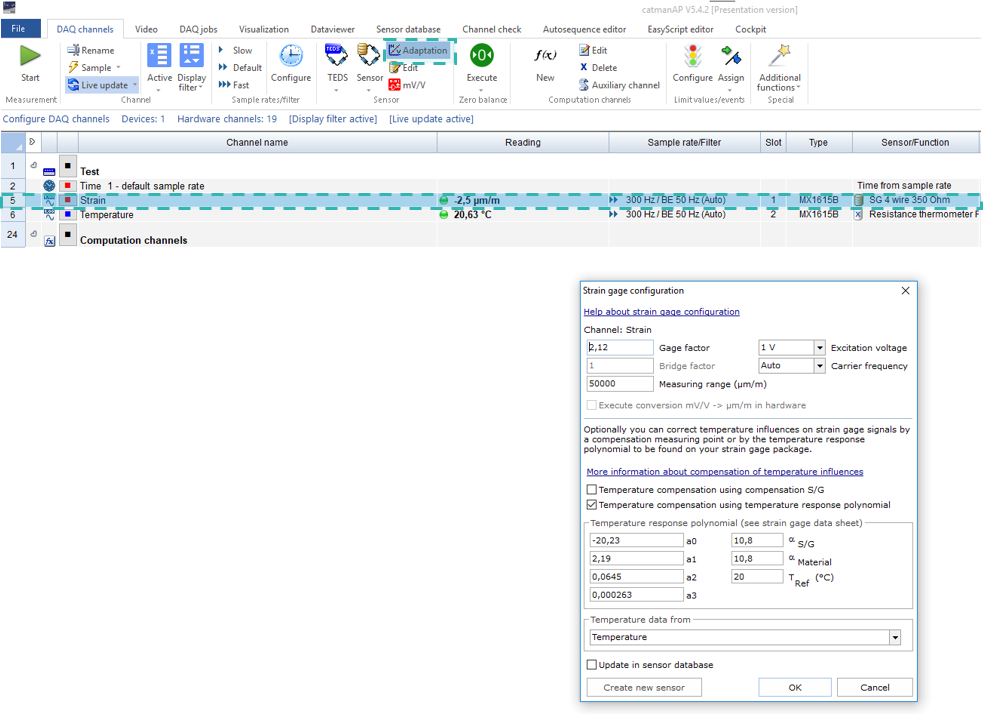
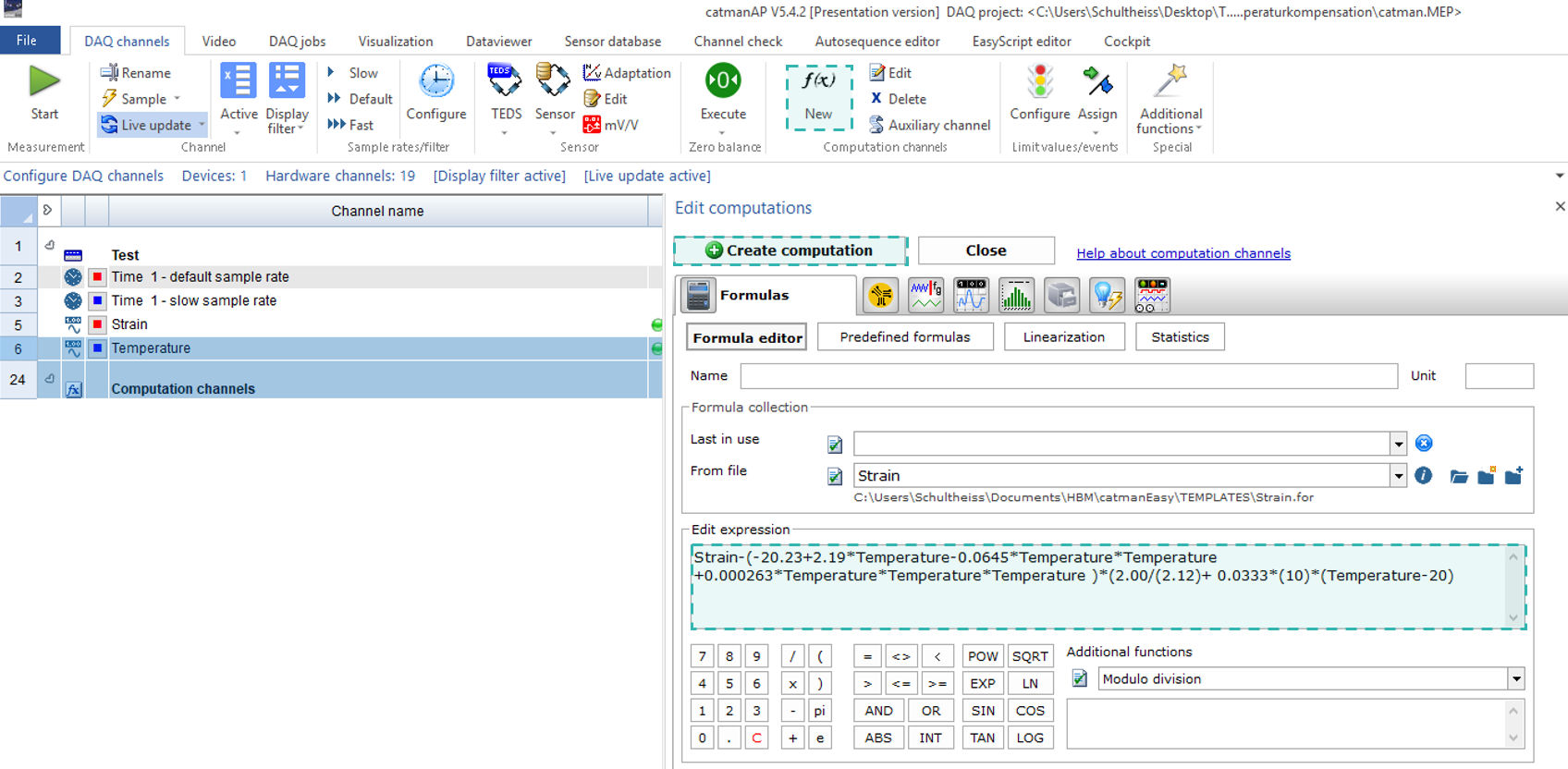
En nuestro ejemplo de aplicación, toma la forma siguiente:

Supongamos que la temperatura durante la medición de la deformación se mantiene constante a 100 °C(T = 100 °C) y que la longitud de los cables es de 10 mm(L = 10 mm). Debe tenerse en cuenta que la longitud de los cables puede variar. A la vista del polinomio, la deformación térmica es superior a 100 μm/m y tiene un impacto significativo en el resultado.
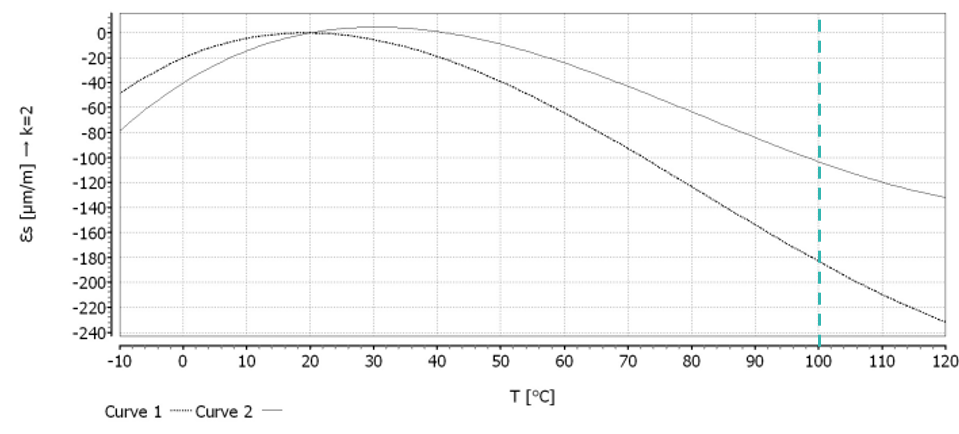
Para calcular la deformación debida a influencias térmicas, aplicamos al polinomio la temperatura y la longitud de los cables:
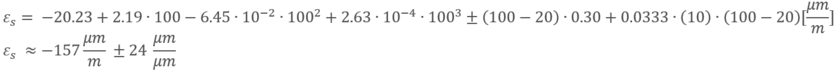
El resultado se corresponde bastante bien con el polinomio que se representa en la hoja de características. El polinomio permite tener en cuenta las influencias más significativas. La única influencia adicional significativa en el resultado sería el uso de cables de 2 hilos muy largos. Pero como utilizamos tecnología de 3 y 4 hilos que compensa el impacto de la resistencia del cable, esa parte del cálculo no es relevante.
Si le restamos la deformación térmica a la deformación medida, obtenemos un valor de deformación corregido, que solo contiene la deformación mecánica: