Il trasformatore viene usato in molte applicazioni diverse ed è uno dei componenti più importanti della tecnologia che usa la corrente alternata. Viene usato nella tecnologia a corrente alternata per effettuare trasformazioni tra diversi livelli di tensione. Per garantire una trasmissione efficiente dell’energia in questi casi, è necessario garantire una buona efficienza e un utilizzo ottimale.
Nonostante la netta prevalenza di circuiti elettronici di potenza, il trasformatore è ancora indispensabile negli alimentatori di piccole dimensioni per consentirne il necessario isolamento galvanico. Viene usato nella tecnologia di misura per convertire le grandezze di misura. A seconda dell’uso a cui sono destinati, i trasformatori devono soddisfare requisiti diversi. Per adattarli a tali requisiti, è indispensabile selezionare in maniera accurata il materiale del nucleo e variare la geometria del nucleo.
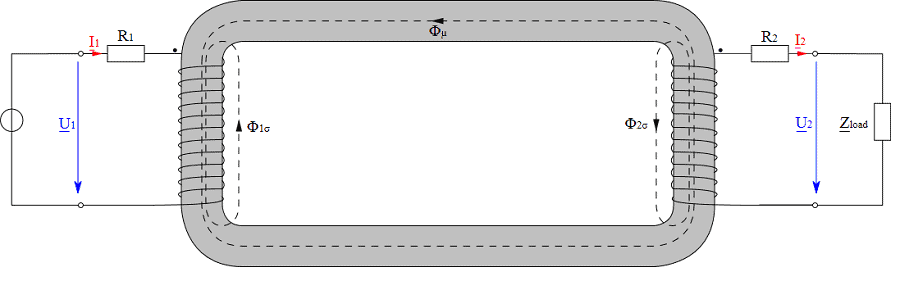
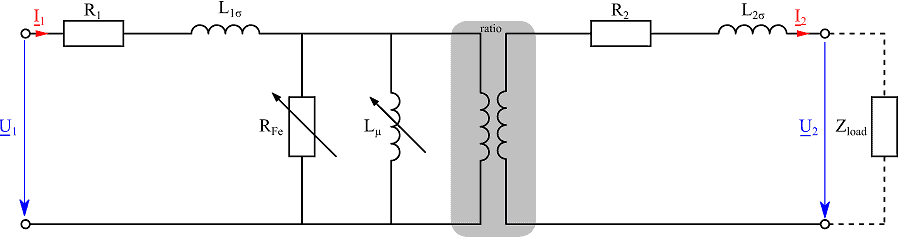
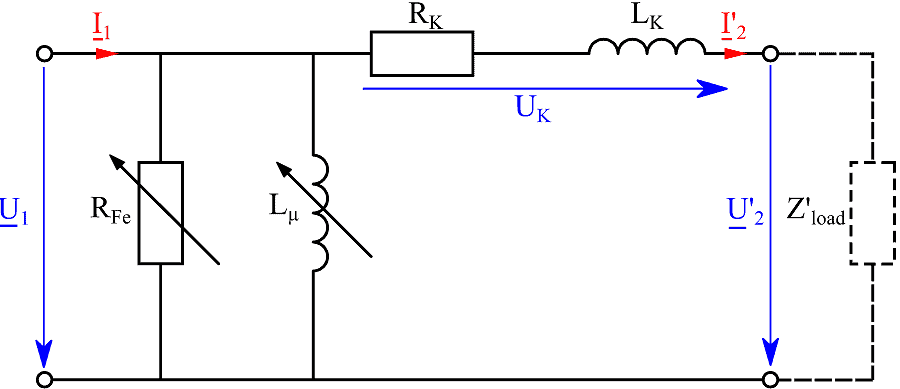
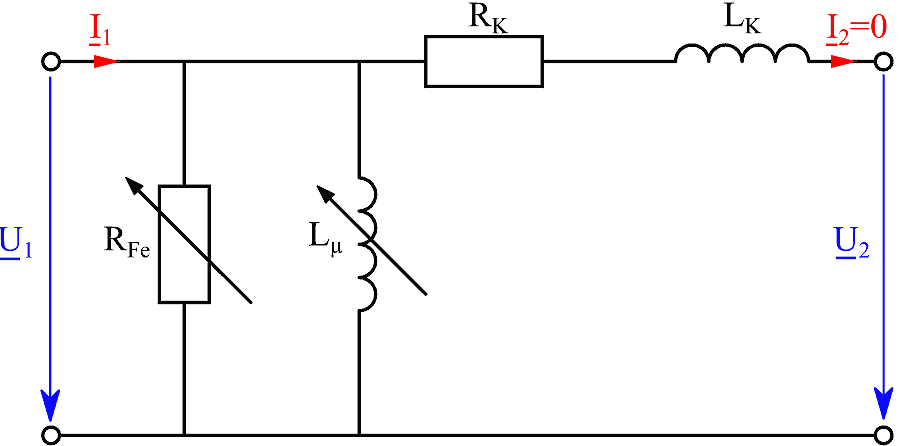
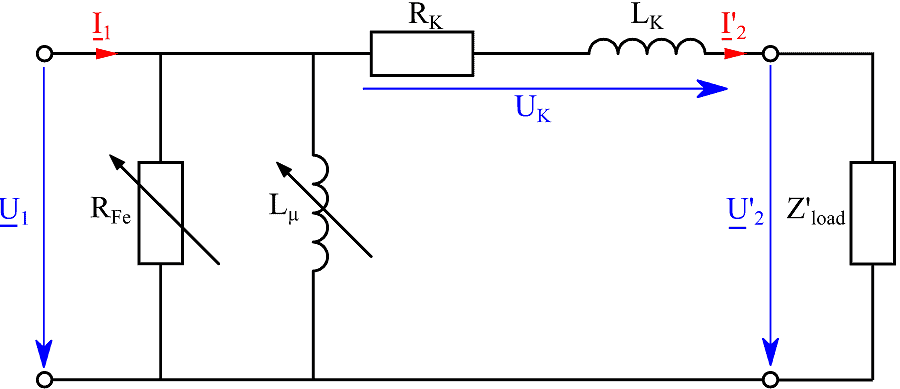
Le proprietà del singolo trasformatore possono essere rappresentate tramite un semplice schema elettrico equivalente che può essere utilizzato per valutare se il trasformatore è adatto a una determinata applicazione e prevedere il suo comportamento in diversi punti di carico.
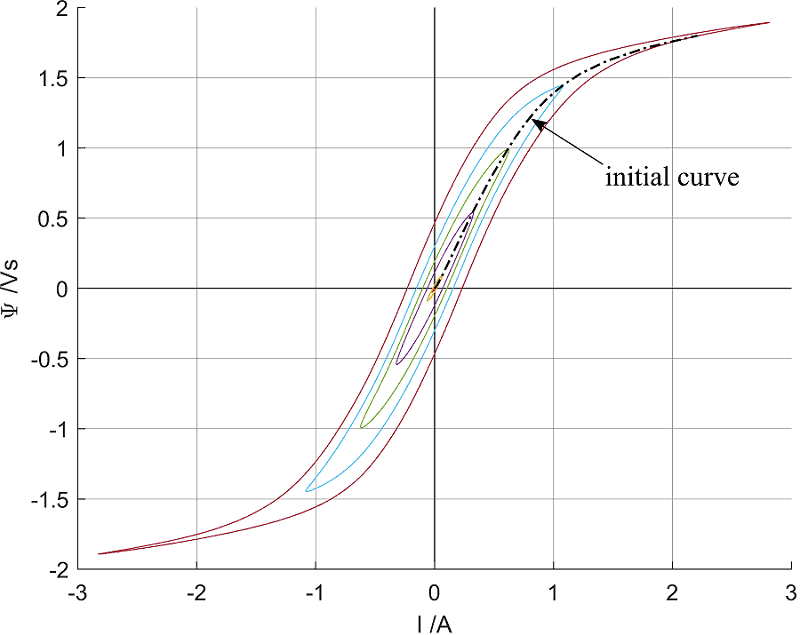
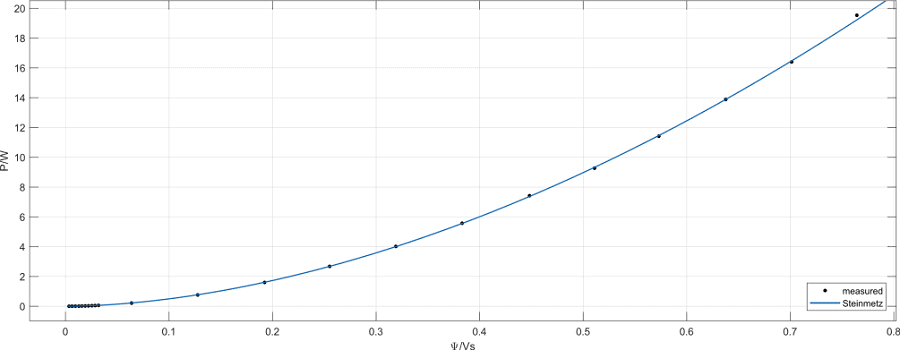
Questo articolo rappresenta e spiega lo schema elettrico equivalente di un trasformatore e presenta nuovi metodi di misura e calcolo per la definizione dello schema elettrico equivalente e delle perdite di ferro nel nucleo del trasformatore. Le misurazioni e i calcoli sono eseguiti con il registratore di dati Gen3i di HBM. In appendice sono raccolte tutte le formule necessarie che possono essere importate in Perception