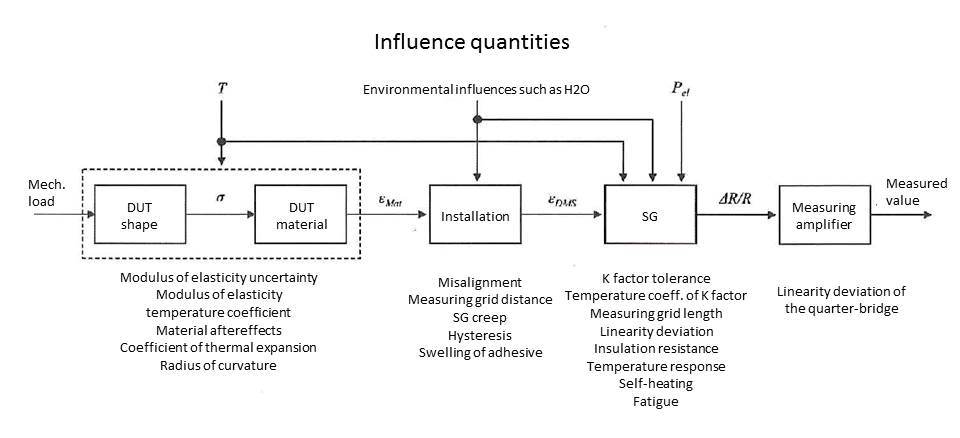
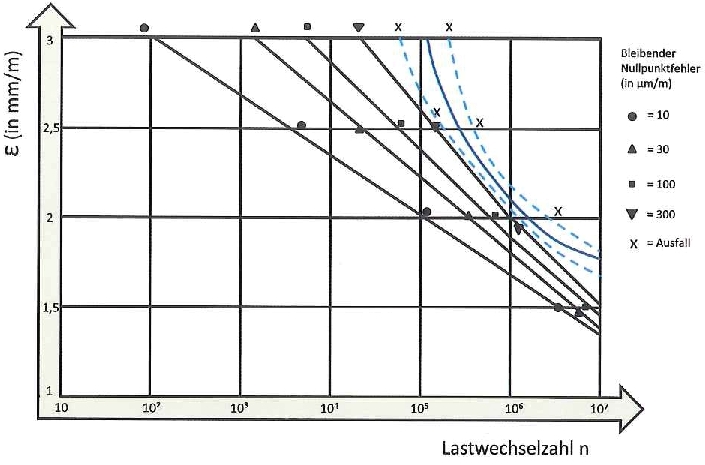
在这些测量中,零点很重要。通常包括建筑物的长期测量和构件的疲劳试验。这种类型的测量任务中零点如果发生变化,将产生一个额外的测量误差。
被测对象的热膨胀,应变片的温度响应
被测材料具有热膨胀系数。热膨胀不会被测量,而只是作为温度对测量结果的影响量。测量栅丝还具有热膨胀系数以及特定电阻的温度系数。由于实验应力分析只对加载引起的应变感兴趣,因此提供的应变片适用于特定材料的热膨胀。然而,所有这些温度系数本身就是由温度引起的变化量,因此不可能完全补偿。无法完全补偿的偏差 ΔƐ 可通过多项式进行计算。由制造商将会在应变片包装标明此多项式的系数,并且每个批次之间会有差别。
这里采用 HBM LY-6/120 作为示例:
剩余偏差(表观应变)以 μm/m 为单位确定。对于30°C的温度,产生的表观应变为-4.4μm/m。
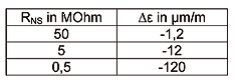
如果环境温度与参考温度(20°C)的偏差较大,或者应变片调整不当,则会出现更大的偏差。但可以通过计算(在线计算)消除。另一方面,该方程显示出每开尔文温差增加 0.3μm/m 的不确定性。在30°C的温度下,多项式的不确定性为3μm/m。
校正计算仅需要材料的热膨胀系数和环境温度。
 自热
自热
这是指应变片在测量过程中,由供电导致的测量栅丝的温度升高,热输出量方程如下::

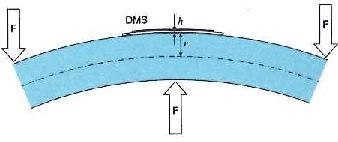
对于均方根值 5 V 的桥路激励电压和120Ω 应变片,产生的热输出为52 mW。对于涂了一层薄薄的粘合剂,测量栅丝长度为6 mm的应变片能够充分散发热量。然而,应变片和测量对象之间会产生一个小的温差,这将导致一个明显的应变(见上文):

如果应变片温度仅比材料温度高一开尔文,则会产生 -11μm/m(铁素体钢)或-23μm/m(铝)的表观应变。测量的不确定度可以通过一个简单的实验粗略确定——在施加负载的情况下连接励磁电压。在温度升高阶段,测量值将略微漂移(零漂)。在热补偿过程中,测量值之间的最大差异大致对应于最大预期偏差。
较低的激励电压产生的热量更低(1 V只产生2 mW)。高电阻的应变片在这方面具有优势。
对于导热性差的部件(塑料等),当使用非常小的应变片时,降低激励电压是必不可少的。在快速变化的温度下工作时,务必小心。