我们将通过一个实例来说明如何在考虑最重要影响的情况下建立四分之一桥路的热补偿。我们采用以下配置：
- 应变片: 1-LY11-10/120 应变片，安装在100°C试验条件下试验箱中的材料上。为了将传感器与放大器连接，使用10mm引线、焊接端子和4线电缆。
- 放大器: QuantumX MX1615B 模块采用四分之一桥路配置，根据电磁环境不同，可使用直流或载频激励值。
- 软件: catman Easy/AP DAQ, 安装在PC机上或在数据记录仪中运行，通过在线数学功能来校正温度影响
应变四分之一桥温度补偿的理论与实践
为了确保在不断变化温度条件下获得准确的测量结果，需要对应变四分之一桥进行温度补偿。有几个 温度因素 会影响测量结果，例如：
- 材料热膨胀差对基底材料和测量栅丝材料的相互影响
- 引线的电阻
- 应变片自加热时应变系数的温度依赖性
- 杨氏模量的温度依赖性
这些温度影响可通过为应变测量而设计的软件包（如HBK的catman Easy/AP）进行校正。
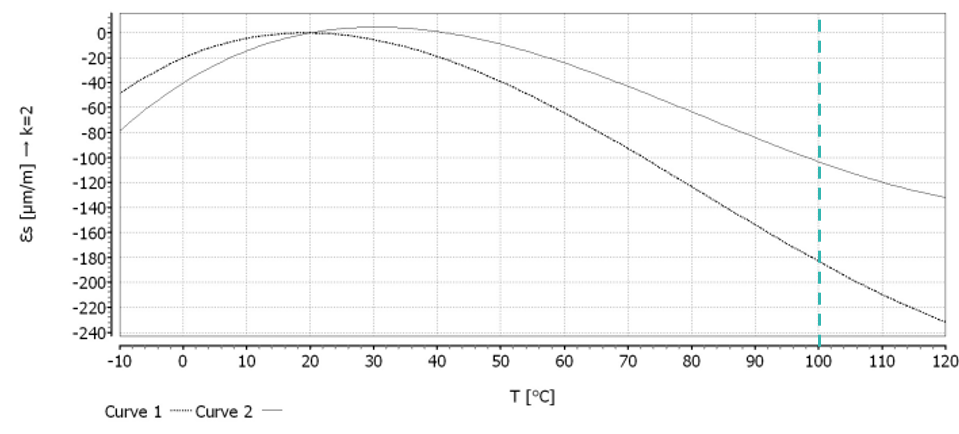
HBK 应变片随附的数据表包含所有相关参数，以确保测量的准确性。数据表中图表和公式中显示补偿参数。注意：在本例中，数据表中显示两条曲线。一条曲线表示应变片本身的热响应，而另一条曲线表示应变片（包括2线引线）的热响应。
应变片的温度响应取决于：
- 基底/材料的温度膨胀系数
- 应变栅丝的温度膨胀系数（CTE）
- 应变片栅丝电阻的温度系数
- k系数
在实际工作中，室温条件下简单地测量和提取热输出应变。测量结果反映了：
- 应变片特性对基底/材料温度膨胀的补偿
- 一种无法补偿的残余误差，但为了达到高精度的测量要求而需要加以校正
残余误差可通过测量确定，并用多项式εs表示，理想情况下，无论温度如何，其结果始终为零。但实际上，在参考温度附近有一个范围，在应变片生产过程中，它被优化到接近于零。
应用实例
1. 用多项式校正应变值
热多项式 绘制在每个数据表上。总体布局如下-请注意，多项式可能有所不同：
在catman Easy/AP中，通过点击DAQ通道的带状条中的“自适应”，可以很容易地添加应变片的热补偿。所有参数见数据表。
在某些情况下，多项式还包括在温度变化时影响应变信号的因素：
- 引线的影响 (εl): 在这个具体示例中，还添加了测量不确定度和连接到测量栅丝应变片引线的影响。一般来说，必须考虑引线的影响，但在应变片类型和制造商之间可能会有所不同。如果您使用的是我们 HBM 3- 或 4-线专利技术，其可补偿所有电缆电阻的影响，但在某些情况下，2线部分不能自动补偿。
- 测量不确定度 (εu): 测量不确定度是总计算中应考虑的一般部分。甚至多项式也有一些导致了不确定性的分散项。
适用的多项式如下：
在本例中，多项式如下：:
假设应变测量期间的温度恒定为100°C（T=100°C），引线长度为10 mm（L=10 mm）。请注意引线的长度可能导致结果会有所不同。从多项式的角度看，它表明热应变对结果有很大的影响，因为它高于100μm/m！
为了计算热输出应变，将温度和引线长度部署到多项式中：
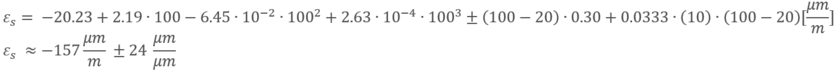
结果与数据表上显示的多项式非常吻合。通过多项式，考虑了最显著的影响，而只有非常长的2线电缆才会产生额外的影响。因为我们使用3线和4线技术来补偿电缆电阻的影响！
将热应变叠加在测量应变上，即可得到校正应变值，该值仅考虑机械应变：
2. 应变系数调整
大多数制造商的多项式是用k=2的系数（或k系数）来测量的，而实际测量中，k系数通常是不同的。这种效应主要在极端条件下出现，如高温和低温或高应变。为了补偿可能影响温度补偿的变化，应考虑对数据表中应变系数进行调整。
因此，乘以数据表应变系数的商，可以校正应变片预期的热输出。在这种情况下，我们通过以下公式调整系数：
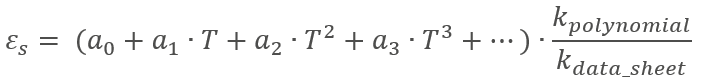
当然，热应变校正仅适用于多项式，不可用于测量不确定度或引线影响：
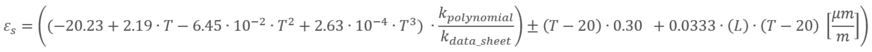
在这种情况下，两个K 系数 (kpolynomial = 2.0 和 kdata_sheet = 2.12)。热应变校正应为：
修正后的应变信号为:
为了在catman数据采集软件中建立这种校正，需要创建一个考虑所有因素的新计算通道。可以通过单击“新建计算通道”和“创建新通道”来添加计算通道。通过在新计算通道的“编辑表达式”中插入热应变校正多项式，可以对应变信号进行校正。
3. 基底材料的偏离温度系数
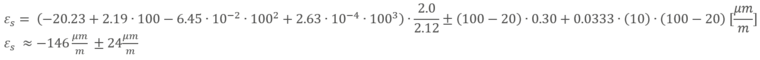
在这个理论测试案例中，应变片的温度系数与材料完全匹配。然而，在实践中，基底材料的温度系数和应变片所适应的温度系数之间可能存在微小的偏差。下式给出了测量应变值的近似调整。在这种情况下，我们假设适用于铁素体钢（10.8 ppm/K）的应变片用于铝（23 ppm/K）：
必须根据参考温度和试验期间的温度计算温差。参考温度是应变片数据表所指的温度，并测量了其参数：
这将导致以下修正系数：
如果将其考虑为校正应变值，则得到整体方程：
为了在catman DAQ软件中建立这种校正，需要创建一个新的计算通道或调整一个已经存在的计算通道。在这个应用例子中，已经存在的计算通道需要更新的热应变校正多项式来进行调整。
4. 温度对K系数的影响 (可选)
第二章通过多项式和K系数拟合进行了应变修正。这对于大多数实验测试来说已经足够了。然而，在很宽的范围内，K系数随温度近似线性变化。因此，可以在未校正的应变信号中考虑K系数校正（不在多项式中考虑，因为K系数的温度依赖性已经包括在多项式中）。温度系数可以是正的，也可以是负的，这取决于栅丝材料（康铜或铬镍（Modco））。
为了方便地计算温度调整K系数，HBK数据表显示了温度系数以及所需的K系数 (kdata_sheet = 2.12)。请先检查线性度是否在极端温度下有效。在这种情况下，K系数温度系数为：
K系数的修正公式如下（T=100°C）:
很明显，这种影响非常小，所以这种影响是可以忽略的。
在catman数据采集软件中，通过调整已有的计算通道，可以很容易地将K系数温度依赖性作为完整公式的一部分。
5. 最终热校正公式
考虑到本技术说明中所述的所有影响，应变值修正公式如下：
6. 词汇表
| ε | 无热校正的应变信号 |
| εs | 应变片数据表的热输出多项式 |
| εc | 包括热校正在内的应变值 |
| εf | 温度系数的失配校正 |
| αR | 应变片电阻温度系数[1/K] |
| αS | 基底/结构的温度系数[1/K] |
| αM | 应变计金属栅丝的温度系数[1/K] |
| k | 应变片的K系数 |
| kdata_sheet | 应变片数据表中的K系数 |
| kdata_sheet(T) | 应变片数据表中包括热校正的K系数 |
| kpolynomial | 用于确定多项式的K系数（通常为2.00） |
| αk | K系数的温度系数 |
| a0 | a0 多项式系数 |
| a1 | a1多项式系数 |
| a2 | a2 多项式系数 |
| a3 | a3 多项式系数 |
| ∆T | 应变测量时的温差和应变片数据表上的参考温度 |
| Tref | 应变片数据表上的参考温度 |
| αsubstrate | 应变片测量材料的温度系数 |
| αstrain_gauge | 应变片温度系数 |
法律免责声明：来自HBK的技术说明旨在为特定主题提供一个快速概述，而不是标准文档。技术说明不断改进，因此经常更改。HBM对描述的完整性不承担任何责任。我们保留随时更改的权利，恕不另行通知。